32 Возможная работа силы. Идеальные связи

Возможной работой силы называется работа силы на любом возможном перемещении точки ее приложения: .

Связи называются идеальными, если возможная работа реакций связей на любом возможном перемещении системы из любого ее положения равна нулю.

Для одной точки и одной связи: , то есть реакция перпендикулярна любому перемещению точки.

Идеальные связи характеризуют: абсолютно гладкие поверхности, нерастяжимые нити, цилиндрические и сферические шарниры, качение по твердой шероховатой поверхности без скольжения.

33 Обобщенные силы. Способ вычисления обобщенных сил

Запишем выражение для возможных работ всех сил, прилож. к точкам системы, через обобщ. коорд.:

, тут .

Обобщ. силой, соотв. некоторой обобщ. координате, называется скалярная величина, равная коэффициенту при вариации этой обобщ. координаты в выражении возможной работы всех активных сил, действ. на механическую систему.

Аналитический способ: (1)

Система с числом степеней свободы >1:

Системе можно сообщить такое возможное перемещ., при котором изменяется одна обобщ. координата , соотв. искомой обобщ. силе . Возможное перемещ. этой обобщ. координаты не равно нулю 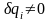, а остальные равны нулю.

Индекс i означает, что возможная работа сил, соотв. вариации только i-ой обобщ. координате.

Силы потенциальные:

Пот. сила: , подставим в (1): - частная производная силовой ф-ции по i-ой обобщ. координате. Тогда: .

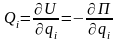34 Принцип возможных перемещений

Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю.

Доказательство необходимости:

Система мат. точек, удовл. принципу возможных перемещений, наход. в равновесии. Докажем, что выполн. равенство: . Если система в равновесии => любая точка системы в равновесии. Сумма активных сил и реакций связи , прилож. к каждой точке системы, должна быть равна нулю: , 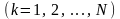. Из этого следует, что и работа этих сил на любом возможном перемещении также равна нулю: , .

Просуммирует по k и раскроем скобки: . в силу идеальности связей => . *необходимость доказана*

35 Условие равновесия сис-мы в обобщенных координатах. Случай потенциальных сил

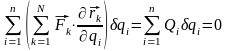Н а систему из N материальных точек наложены связи, удовл. принципу возможных перемещений. Запишем: (1). Система имеет n степеней свободы => ее положение опред. n обобщ. координатами , а радиус-вектор , k-ой точки: . Возможное перемещ. каждой точки: (2). Подставим (2) в (1): , отсюда получим: (3). Вариации обобщ. координат независимы друг от друга => (3) выполнится, когда все обобщенные силы равны нулю. Условие равновесия голономной системы в обобщ. коорд.: .