9.2. Стохастическая оптимальная линейная система при полной информации о состоянии

Пусть объект описывается уравнением

(9.14)

и задан критерий оптимальности

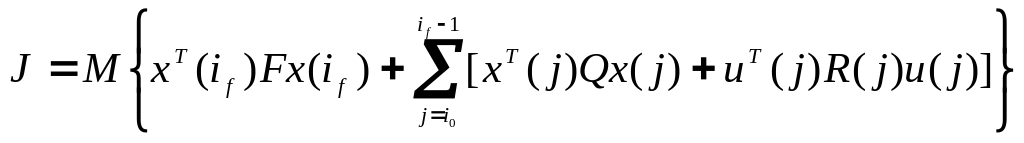, (9.15)

где h(i) - известная функция;

V₀(i) - последовательность некоррелированных случайных величин с нулевым средним и дисперсионной матрицей Q₀(i);

F, Q, R, Q₀ - симметричные матрицы, причем F0, Q0, R>0, Q₀0. Шум V₀(i) не коррелирован с начальным значением x(i₀).

Требуется найти оптимальное управление с обратной связью, т.е. управление, доставляющее минимум функционалу (9.15) при произвольном начальном состоянии объекта. Принимается, что фазовый вектор х известен без ошибки. Эта задача является дискретным аналогом непрерывной задачи (8.39) и отличается от задачи (9.1) – (9.2) тем, что объект подвержен случайному воздействию, и критерий оптимальности представляет собой математическое ожидание от функционала, совпадающего с критерием оптимальности в детерминированной задаче. Ее решение совпадает с решением детерминированного аналога, т.е. стохастическое оптимальное управление определяется соотношениями (9.8), (9.9), (9.10), (9.13).

Для вывода уравнений используется метод динамического программирования.

Функция Беллмана определяется следующим образом

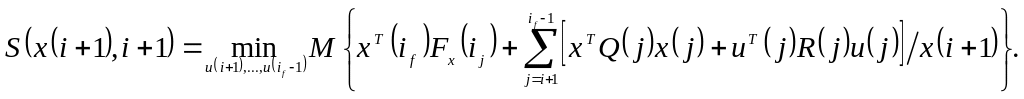
Уравнение Беллмана принимает вид (опускается аргумент i)

или

.

Решение этого уравнения ищется в виде (9.5). После необходимых преобразований можно получить соотношения для оптимального управления, что и в детерминированном случае.

9.3. Наблюдатель (фильтр) Калмана

Задача синтеза стохастической оптимальной системы при неполной информации в дискретном случае аналогична задаче в непрерывном случае (принцип разделения). Рассмотрим задачу оптимальной оценки. Пусть объект и наблюдение описываются уравнениями

, (9.16)

; (9.17)

где V₀(i), V_H(i) - последовательность гауссовских случайных величин с характеристиками:

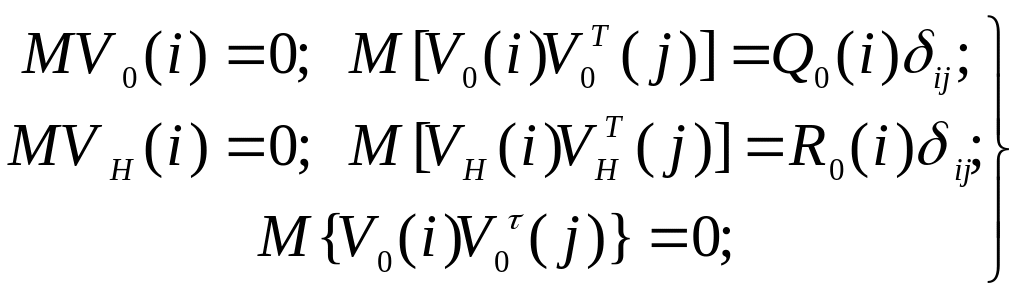, (9.18)

где - символ Кронекера ( =1 при i=j и =0 при ij);

x⁰ - гауссовая случайная величина с характеристиками

(9.19)

где Q₀(i), R₀(i), p₀ - симметричные матрицы, причем Q₀(i)0; R₀(i)>0; p₀0.

Случайные последовательности V₀(i) и V_H(i) называют соответственно шумом объекта и шумом наблюдения или измерения, и они не коррелированны со случайной величиной x⁰.

Требуется, используя измеренные значения переменной y(i) при j=i₀,i₀+1,...,i, найти несмещенную оценку вектора x(i), обеспечивающую минимум квадрата ошибки :

.

Напомним, что оценка называется несмещенной, если . Условие R(i₀)>0 означает, что ни одна координата выходной переменной не измеряется точно (несингулярная задача).

Решение невырожденной задачи определяется следующим образом:

; (9.20)

(9.21)

; (9.22)

; (9.23)

(9.24)

Здесь является математическим ожиданием вектора x(i) и служит его априорной оценкой, т.е. оценкой, которая получается до измерения y(i); - дисперсионная матрица ошибки т.е. ошибки априорной оценки; - дисперсионная матрица ошибки т.е. ошибки искомой (апостериорной) оценки.

Выражение для оценки содержит, кроме априорной оценки, поправочный член, пропорциональный невязке - разности между измеренным значением переменной y(i) и ее оценкой. При вычислении оценки на каждом шаге нужно начинать с определения априорной дисперсионной матрицы . Далее нужно вычислить матрицу коэффициентов усиления k⁰(i) и дисперсионную матрицу , затем априорную оценку и в последнюю очередь искомую оценку .Так, матрицы , , и k(i) не зависят от измерений, их можно вычислить заранее при всех необходимых значениях .

Соотношения (9.20) - (9.24) впервые получены Калманом, поэтому оптимальный дискретный линейный фильтр называют фильтром Калмана.

Установим физический смысл и роль k⁰(i). Для этого рассмотрим случай когда x(i) и y(i) являются скалярными и c(i)=1. При этом соотношения (9.20) - (9.24) принимают вид:

Пусть k⁰(i)=0. В этом случае и изменение, производимое в i-ый момент, не используется, так как оно не несет никакой информации, т.е. дисперсия его ошибки очень велика

Если k⁰(i) = 1, то , т.е. оценка определяется полностью последним измерением. Измерения, производимые до i-го момента, а также другая априорная информация никак не используются. Такая ситуация возникает, когда i-е измерение производится без ошибки, или когда очень велики дисперсии ошибки до i-го измерения (или дисперсии шума объекта).

Таким образом, выбором величины k⁰(i) регулируется влияние априорной и текущей информации на определение оценки . Задача оптимальной оценки состоит в выборе такого k⁰(i), при котором наилучшим образом используется алгоритм и текущая информация.

Вывод равенств (9.20) - (9.24) начнем с введения равенства

где .

Уравнение (9.21) непосредственно следует из (9.16). Вычитая (9.21) из (9.11), находим

или

.

Так как и V_H(i) независимы, то из последнего соотношения следует первая часть равенства (9.23).

Остается доказать, что средний квадрат ошибки V₀(i), равный следу матрицы p(i), принимает минимальное значение, если в (9.20) матрица k⁰(i) определяется соотношением (9.22). Для этого первую часть равенства (9.23) представим в виде

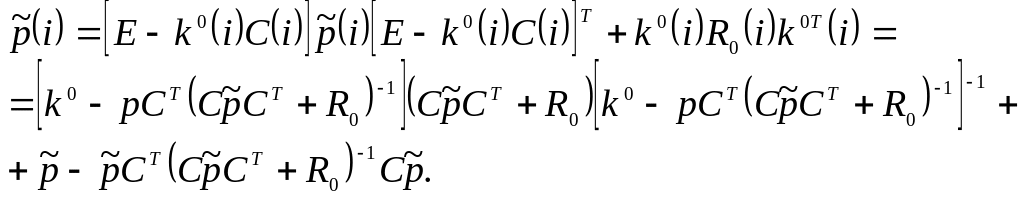(9.25)

Если k⁰ определяется из (9.22), первое слагаемое правой части последнего равенства обращается в нуль. Оставшуюся часть обозначим :

Эта матрица, в силу свойств дисперсионных матриц, неотрицательно определена, p  0, следовательно, ее диагональные элементы неотрицательны (последнее следует из неравенств ). Эти элементы получаются из условия при где – диагональные элементы матрицы p. Так как матрица то последнее слагаемое в (9.25) не меньше нуля при произвольной матрице k⁰. Поэтому след матрицы p будет минимальным при такой матрице k⁰ , когда первое слагаемое в (9.25) обращается в нуль, т.е. когда k⁰ определяется (9.22). При этом из (9.25) получаем вторую часть равенства соотношения (9.23).