5.3. Наблюдатели

Поставим задачу построения такого уравнения, называемого наблюдателем, решение которого m(t) сходится к x(t) при любых начальных условиях x(0) и z(0) в смысле

(5.18)

Рассмотрим задачу наблюдения системы (5.1)-(5.2), которая характеризуется постоянными матрицами A и C и которая является наблюдаемой системой, т.е. rank H=n. Определим наблюдатель полного порядка с помощью линейного уравнения

(t)=Az(t)+V(t)(y(t)-Cz(t)), t0. (5.19)

Требуется найти такую матрицу V(t) размера nm, чтобы выполнилось условие (5.19). Обозначив через (t) ошибку оценивания

(t)=x(t)-z(t). (5.20)

Продифференцируем уравнение (5.20) по t и подставим в неё выражения из формул (5.1) и (5.19). В итоге получим уравнение для ошибки (t)

(t)=[A-V(t)C] (t). (5.21)

Известно [6], что если rank H=n, то V(t) можно выбрать постоянной и такой, что собственные значения (A-VC) принимают заранее заданные значения такие, что имеют отрицательные действительные части. Тогда будет справедливым соотношение (5.18).

Действительно, общее решение уравнения (5.21) имеет вид

,

где отрицательные действительные части собственных значений матрицы обеспечивают при для всех , независимо от (см. Приложение 1).

Для неоднородной системы (5.11) – (5.12) наблюдатель полного порядка описывается соотношением

=A(t)z(t)+B(t)u(t)+V(t)(y(t)-C(t)z(t)). (5.22)

При этом ошибка оценивания (5.20) удовлетворяет тому же уравнению (5.21).

Поставим теперь задачу построения наблюдателя для наблюдаемой системы (5.11)-(5.12) с учетом уже имеющегося уравнения измерения (5.12).

Пусть A и C постоянны, D=0, rank H=n, a rank C=p0. Тогда выберем матрицу W размера (n-p)n так, чтобы квадратная матрица L размера nn, равная

, (5.23)

была невырожденной. Обозначим F и G блоки обратной матрицы L^-1=(F, G), где F имеет размер nр, a G-n(n-p). Очевидно, что LL^-1= L^-1L=E, где Е-единичная матрица и всегда можно записать:

а следовательно, для блоков матрицы и можно записать

.

Например:

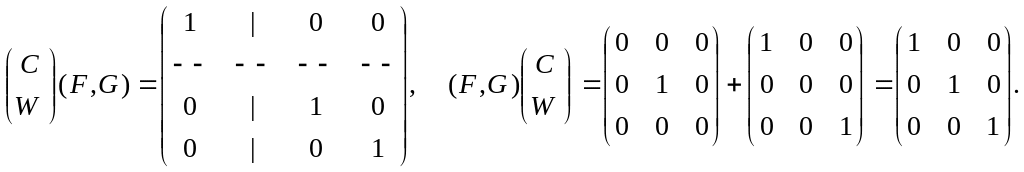
Тогда введем дополняющий вектор (t)R^n-p такой, что (y(t), (t))^T =Lx(t) или

(5.24)

Требуется оценить вектор (t). Поэтому из (5.23) и (5.24) имеем

.

После дифференцирования второго уравнения, подставляя вместо и выражения из (5.11) и (5.24), получим

, (5.25)

где величина ₀ произвольна. Уравнение (5.25) не обеспечивает сходимости правой части (5.24) к x(t). Действительно, пусть и ошибка оценки тогда равна (t)=x(t)-(Fy(t)+G(t)). Дифференцируя её, получим

Используя соотношение FС+GW=E уравнение для преобразуем к виду

Ранги матриц G и W не превосходят n-p, поэтому в силу неравенства Сильвестра ранг матрицы GWA тоже не больше n-p.

Так как определитель матрицы равен произведению её собственных чисел, а матрица GWA вырождена, то она не может быть гурвицевой. Это означает, что (t), вообще говоря, не стремится к нулю при t, а следовательно, формула (5.24) не обеспечивает требований, предъявленным к наблюдателям. Поэтому введем ₁(t)R^n-p как оценку вектора (t) соотношениями, вытекающими из (5.25) и выражения для :

,

где , , , , и, подставляя эти выражения в верхнее, получим:

(5.26)

Воспользуемся преобразованиями, чтобы доказать сходимость ₁(t) к (t). Учтем ещё раз, что

Тогда выражение (5.26) приобретает вид

Вычитая полученное выражение из (5.25), получим

(5.27)

Обозначив (t)=(t)-₁(t) для ошибки оценки (t), получим уравнение

(5.28)

в котором матрица V подлежит определению на условиях сходимости оценки ₁(t) к (t), т.е. из условия (t)0 при t. Это условие требует выбора матрицы V таким образом, чтобы матрица (W-VC)AG была гурвицевой.

При сделанных предположениях постоянную матрицу V размера (n-р)р можно выбрать так, чтобы тривиальное решение уравнения (5.28) было экспоненциально устойчиво относительно начальных возмущений [23]. Это означает, что .

Теперь оценку вектора зададим в соответствии с (5.24)

z(t)=Fy(t)+G₁(t), (5.29)

откуда с очевидностью следует, что (x(t)-z(t))0 при t.

Если возникает затруднение с определением для (5.26), то можно использовать замену ₂(t)=₁(t)-Vy(t). Тогда из (5.29) получим оценку в виде

z(t)=G₂(t)+(F+GV)y(t), (5.30)

а уравнение для ₂(t) с учетом (5.27),(5.2),(5.11) имеет вид

(5.31)

где начальное значение произвольно.

Из соотношений (5.24), (5.30), (5.29) следует, что для ошибки оценивания ₁(t)=x(t)-z(t) справедливо равенство

а следовательно, (5.31) определяет наблюдатель для системы (5.11). Так как фактически для оценки x(t) мы используем вектор размерности n-р, то соответствующий наблюдатель называется наблюдателем пониженного порядка (наблюдателем Люенбергера).

Обобщая наши обсуждения, запишем алгоритм построения наблюдателя Люенбергера:

1. Выбираем матрицу W так, чтобы L в (5.23) была невырожденной.

2. Представляем L^-1 в виде L^-1=(F,G), где F –матрица размера np, а G-размера n(n-р).

3. Определяем матрицу V так, чтобы матрица (W-VC)AG была гурвицевой, т.е. чтобы все ее собственные значения имели отрицательную действительную часть.

4. Находим решение ₂(t) из (5.31).

5. Определяем оценку z(t) вектора x(t) из (5.30).

Если возможно вычисление производной , то в п.4 находят решение для ₁(t) из (5.26), а в п.5. находим оценку z(t) из (5.29).

Для построения наблюдателя полного порядка необходимо выполнить шаги:

1. Из уравнений, описывающих систему, составляем матрицу , где элементы матрицы 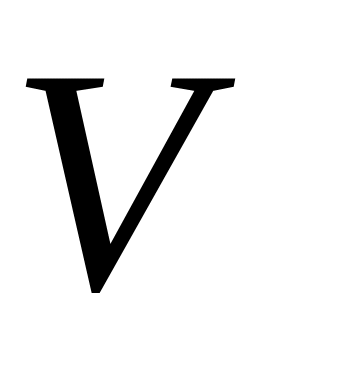подлежат определению;

2. Определяем собственные значения матрицы как функции элементов из уравнения

.

3. Находим такие , чтобы действительные части собственных значений матрицы были отрицательны.

4. Подставляем найденную матрицу в уравнение полного наблюдателя.

Пример 5.3. Построим наблюдатели для системы

Для рассматриваемой системы запишем

Для построения полного наблюдателя, воспользуемся выражением (5.21) и найдем матрицу V=( ₁, ₂)^T такую, чтобы собственные значения матрицы (A-VC) имели отрицательные действительные части.

Из последнего равенства следует, что ₁, ₂0 и можно принять ₁=₂=2, а следовательно ₁₌₂=-1. Таким образом, уравнение нашего наблюдателя имеет вид из (5.22)

При построении наблюдателя пониженного порядка учтем уравнения измерения y=x₁. Тогда n=2, р=1. Найдем матрицу W для (5.23)

и определим L^-1

Отыскиваем матрицу V (в нашем случае скаляр ) такую, чтобы (W-VC)AG была гурвицевой.

Решение для ₂(t) находим из (5.31)

откуда видно, что первое уравнение сохраняет вид исходного уравнения наблюдения, а второе уравнение использует решение ₂(t). Значение ₂(t) получаем из (5.31)