5.2. Каноническая форма наблюдаемости. Обнаруживаемость

Если ранг матрицы (5.8) равен l (ln), то это означает, что среди всех фазовых координат (n-l) координат являются ненаблюдаемыми (невосстанавливаемыми). Тогда возможно такое преобразование координат, сохраняющее ранг матрицы (5.8), которое приводит к разветвлению системы в целом на две подсистемы – наблюдаемую и ненаблюдаемую.

Составим неособую матрицу линейного преобразования Т точно так же, как и в подразделе 4.2.

Преобразование уравнения состояния и наблюдения принимает вид

,(5.13)

где

. (5.14)

Как и прежде в (4.23) и (4.25), составим

,

где Т₁ состоит из l независимых вектор-строк, составляющих базис в наблюдаем подпространстве , а вектор-строки Т₂ (их всего n-l) составляют подпространство ненаблюдаемости R^n-l. Выбор элементов строк матрицы описан в (4.2).

Повторив рассуждения раздела 4.2, изменяя лишь понятия “управляемость” на “наблюдаемость”, получим:

. (5.15)

В этих выражениях строки матрицы A A_j, j= , не содержащие невосстанавливаемых координат, удовлетворяют условию A_jP₂=0, а для строк, содержащих такие координаты, в общем случае A_jP₂0. (В правых частях 0 означает нуль-вектор). Таким образом, столбцы AP₂ есть векторы, принадлежащие ненаблюдаемому подпространству, а следовательно, T₁AP₂=0. Точно так же можно показать, что остальные блоки в общем случае отличны от нуля. Строки матрицы С принадлежат пространству наблюдаемости, а столбцы P₂ – не принадлежат, следовательно CP₂=0.

Используя полученные результаты для (5.15) и подставляя их в (5.13), получим, предварительно разбив вектор на наблюдаемую часть и ненаблюдаемую –

, (5.16)

где

Таким образом, систему уравнений (5.16) можно записать в виде

(5.17)

откуда очевидно, что не влияет на формирование y(t), а потому и ненаблюдаема.

Схематически рассмотренный случай можно проиллюстрировать структурной схемой на рис. 5.1.

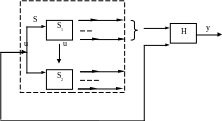
Рис. 5.1. Структурная схема формирования вектора выхода из наблюдения (Н) для не вполне наблюдаемой системы

Для не вполне наблюдаемой системы, представленной в каноническом виде (5.16), матрица наблюдаемости (5.8) приобретает удобный для анализа вид

.

Используя (5.17) для фазового вектора можно записать x(t)=x₁(t)+x₂(t), где x₁(t) – наблюдаемая часть вектора и x₂(t) – ненаблюдаемая. Фазовый вектор x(t) восстанавливается по наблюдениям y(t) и при известном u(t) на интервале [t₁,t₂] с точностью до невосстанавливаемого вектора x₂(t).

Если при отсутствии входных воздействий и ненулевой наблюдаемой составляющей фазового вектора x₁(t) при t ненаблюдаемая составляющая x₂(t)0, то система движется в подпространстве наблюдаемости R_H и вектор состояний всегда может быть восстановлен. Если система (5.11) – (5.12) наблюдаема, то, как следствие, она и обнаруживаема. Обнаруживаемой является и всякая асимптотически устойчивая система.

Из канонической формы наблюдаемости (5.16) или (5.17) следует, что система является обнаруживаемой, если матрица является асимптотически устойчивой, т.е. ее собственные значения имеют отрицательные действительные части.

Пример 5.1. Проанализируем наблюдаемость и обнаруживаемость системы

.

Из условия задачи можем записать

.

Тогда для матрицы наблюдаемости имеем:

Таким образом, система вполне наблюдаема, если параметр а  0. Если же а = 0, то, как видно из уравнения, координата х₁ не наблюдаема.

Для оценки обнаруживаемости используем линейное преобразование Т перестановки координат и получим:

.

Отсюда следует, что собственное значение “матрицы” равно нулю, а система является обнаруживаемой.

Пример 5.2. Оценить наблюдаемость системы

и, приведя ее к каноническому виду оценить обнаруживаемость.

Из условия задачи и произведя расчет А^ТС^Т, (А^Т)²С^Т, запишем:

Очевидно, что система не вполне наблюдаема и ненаблюдаемыми являются первая и вторая координаты.

Выполним преобразование координат Т таким образом, чтобы наблюдаемая координата стала первой, т.е. первая строка в матрице Т равна t₁ = (0 0 1). Чтобы “старая” первая координата стала второй, нужно выбрать t₂ = (1 0 0). Тогда дополняющей строкой для сохранения независимости строк можно записать t₃ = (1 0 0), т.е. вторая “старая” координата становится третьей.

Таким образом, для линейного преобразования получим

,

это так называемая перестановочная матрица ( ). Используя формулы (5.14.), получим:

или в раскрытом виде:

.

Для оценки обнаруживаемости найдем собственные числа матрицы :

Так как оба собственных числа больше нуля, то система необнаруживаема.