4.2. Каноническая форма управляемости

Если объект не вполне управляем, то очевидно, что достижимая область для него есть , где называют подпространством управляемости, а – ранг матрицы управляемости .

Можно легко показать, что свойство управляемости не зависит от выбора системы координат и является фундаментальным свойством, определяемым матрицами А и В для системы (4.8). Однако с помощью преобразования координат можно получать очень удобную для анализа каноническую форму управляемости.

Пусть . Сформулируем неособую матрицу преобразования

,

такую, которая имеет вид

, (4.23)

где

,

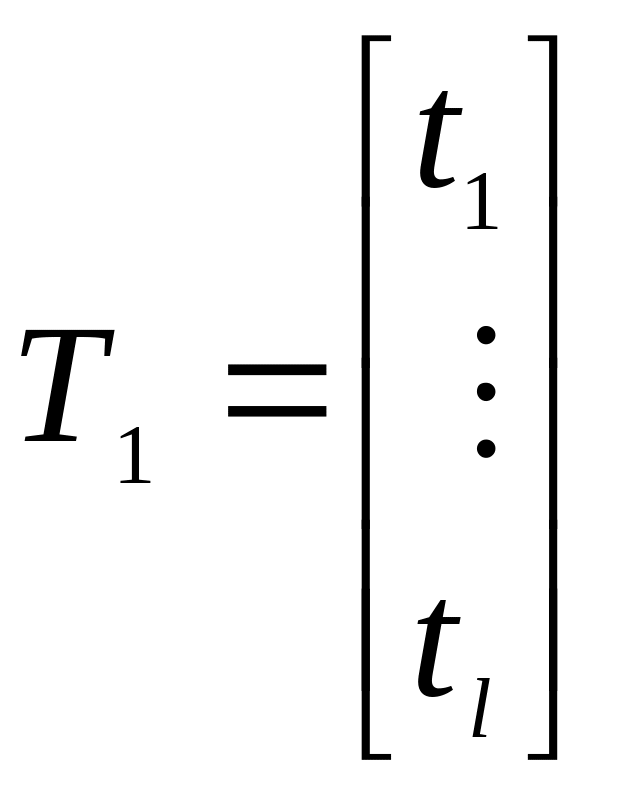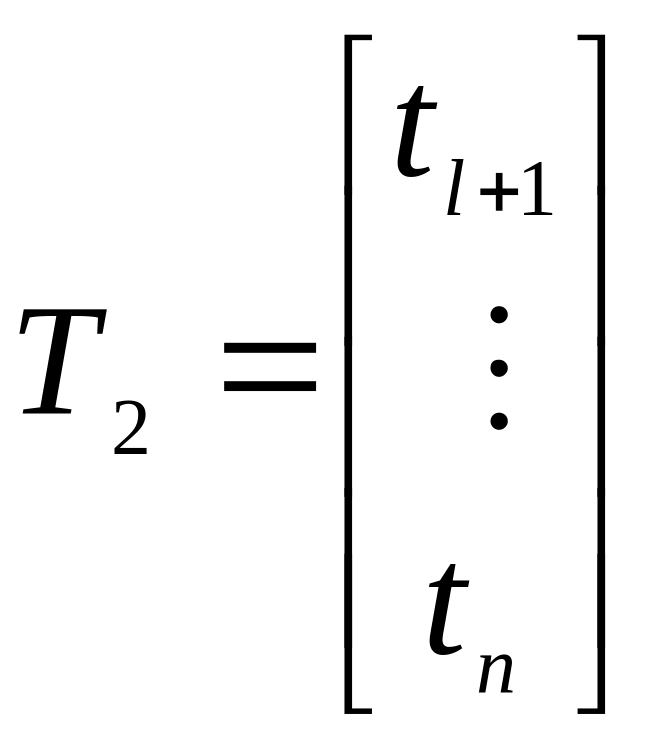
и строки такие, что образуют базис в , а вместе с - базис в .

Обычно в качестве матриц используют перестановочные матрицы, в которых элементы , если мы хотим, чтобы “новая” i-я координата соответствовала j-й «старой», а остальные элементы равны нулю.

Используя преобразование Т, систему (4.16) приведем к виду

. (4.24)

Обратную матрицу , которая существует в силу неособенности Т, запишем в виде , где содержит столбцов, а – (n-l) столбцов. Тогда, учитывая определение обратной матрицы, получим:

,

откуда следует, что

, (4.25)

а значит, любой вектор из принадлежит, а любой из не принадлежит .

Таким образом,

и, как следствие,

, (4.26)

. (4.27)

В (4.26) , т.к. столбцы содержат ненулевые элементы только на местах, соответствующих управляемым координатам, т.е. для каждого столбца можно записать , а для любой строки , в силу определения, . Точно так же можно показать, что в общем случае остальные блоки в (4.26) отличны от нуля.

В (4.27) , т.к. строки , а столбцы .

Таким образом, система (4.24) принимает вид

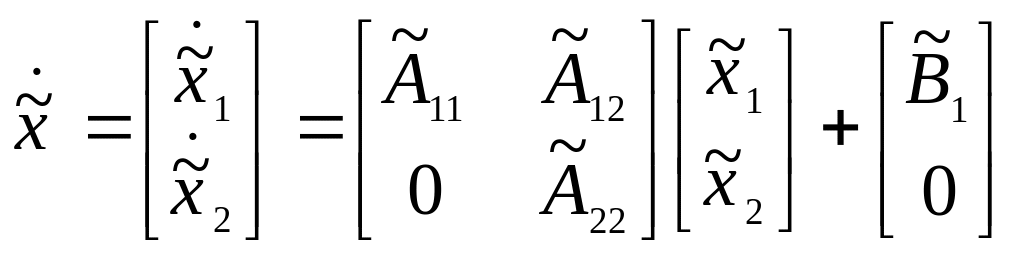, (4.28)

где – подпространство управляемости;

- подпространство неуправляемости;

.

Из (4.28) видно, что зависит от и , в то время как зависит только от , т.е. – независим.

Структурные схемы вполне управляемой и не вполне управляемой систем представлены на рис. 4.1.

а б

Рис. 4.1. Структурная схема управляемой - а и неуправляемой - б систем

Пример 4.1. Для иллюстрации рассмотрим систему:

.

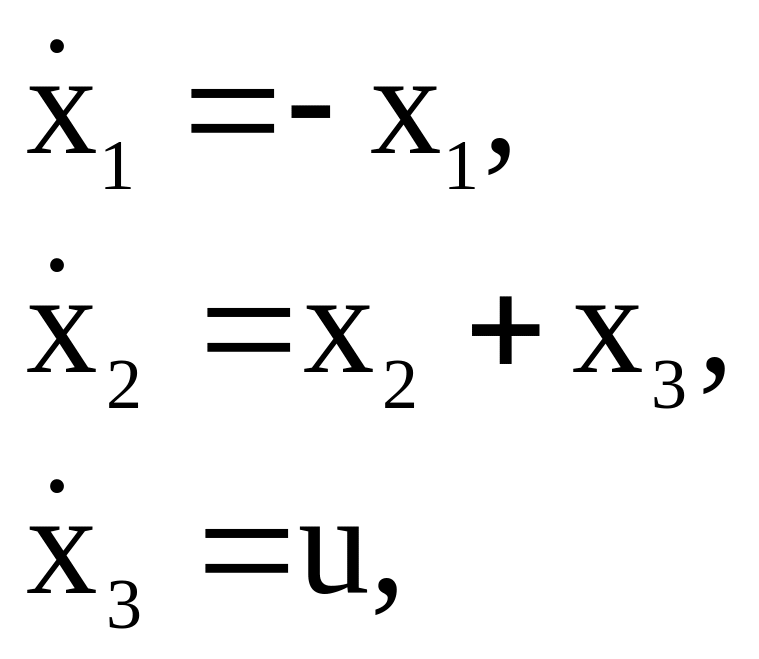
Матрица управляемости и ее ранг равны:

.

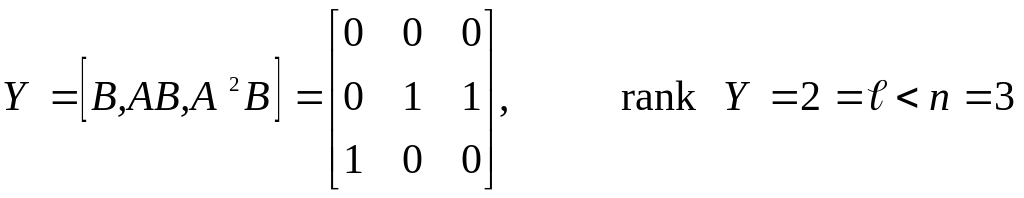Таким образом, система не вполне управляема. Неуправляемой координатой является . Тогда матрицу Т можем выбрать в следующем виде:

.

Далее, используя , получим:

,

,

и окончательно запишем канонический вид системы:

, (4.29)

где – управляемые, а – неуправляема.

4.3. Стабилизируемость

Если система (4.8) не вполне управляема, то ее вектор состояния можно представить в виде

, (4.30)

где – вектор из пространства управляемости , - вектор, ортогональный любому вектору из , и принадлежащий ортогональному дополнению .

Пусть , а в процессе функционирования в момент t система попала в , т.е. .Тогда возникает вопрос, всегда ли необходимо для попадания системы в выполнение условий управляемости.

Оказывается, что для синтеза устойчивой системы управления важна не полная управляемость, а стабилизируемость.

Объект (4.8) называется стабилизируемым, если в (4.30) при .

Очевидно, что вполне управляемый объект является стабилизируемым . Асимптотически устойчивый объект ( при и u(t)=0) также является стабилизируемым.

Для канонической формы (4.28) неуправляемая составляющая удовлетворяет уравнению:

, (4.31)

из которого следует, что система стабилизируема, если все собственные значения матрицы имеют отрицательные вещественные части.

Например, для не вполне управляемой системы из Примера 4.1 получаем , а следовательно, собственное число и, очевидно, система стабилизируема. Действительно, из третьего уравнения в (4.29) получаем , откуда и .

Пример 4.2.Проанализируем управляемость и стабилизируемость системы

.

Из условия задачи можно записать:

, ,

а для матрицы управляемости получим:

, rankY = 1 < n = 3.

Таким образом, система не вполне управляема и, как видно из матрицы Y, неуправляемыми координатами являются координаты х₁ и х₂. Для оценки стабилизируемости произведём линейное преобразование Т таким образом, чтобы управляемая координата х₃ стала первой , - стала второй, а - третьей. Тогда строки нашей перестановочной матрицы Т имеют вид:

, .

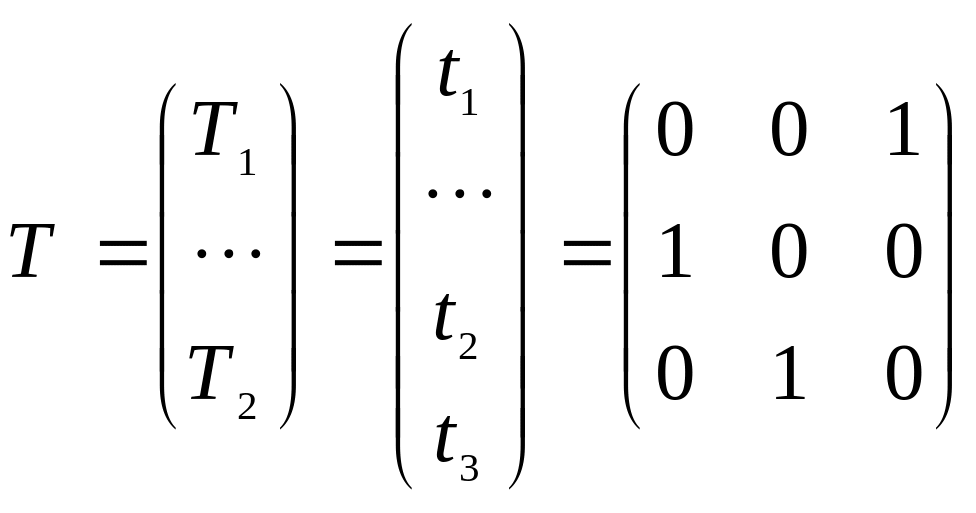Используя формулы (4.26 – 4.28), получим:

; ,

или

.

Для оценки стабилизируемости найдём собственные числа матрицы :

.

Так как оба собственных числа имеют действительную часть больше нуля, то система нестабилизируема.