Рис. 3.3. Схема взаимодействия отраслей

Инвестиции осуществляются из объемов произведенной продукции секторами, которые можно определить с помощью производственных функций (ПФ). Например, для ПФ в форме Кобба-Дугласа зависимость от основных фондов имеет вид:

, , (3.7)

где - константа, которая может зависеть от величины трудовых ресурсов, которые сейчас нас не интересуют.

Будем полагать, что весь продукт, произведенный во 2-м секторе идет на потребление, а продукт 1-го сектора идет на восстановление или расширение основных фондов 1-го и 2-го секторов и частично на потребление (импорт). Тогда можно записать для инвестиций

, , , (3.8)

а для потребления

C(t)=(1 – ) . (3.9)

Объединяя (3.6) – (3.9), уравнения, описывающие состояние системы и ее выход имеют вид

(3.10)

С(t) = (1 ) . (3.11)

В уравнениях (3.10), (3.11) фазовыми координатами состояния системы являются величины , а управляющими параметрами . Отличие уравнений (3.10) и (3.11) от ранее полученных для моделирования других объектов заключается в их нелинейности, которая связана как с использованием переменной в степени, отличной от первой, так и с наличием произведений и .

Чтобы прийти к линейным уравнениям, произведем линеаризацию уравнений вблизи некоторой достигнутой фазовой точки ( , ), например стационарной, в которой . Для этого представим переменные в модели (3.10) – (3.11) в виде:

(3.12)

где , .

Подставив (3.12) в уравнения (3.10) – (3.11) и учтя, что в стационарной точке:

,

в преобразованных уравнениях в связи с относительной малостью и произведем разложения до линейных членов:

и отбросим все члены, содержащие бесконечно малые величины выше первого порядка, т.е. пропорциональные произведениям .

В итоге получим систему уравнений:

= ,

которая в матричном виде может быть представлена как

,(3.13)

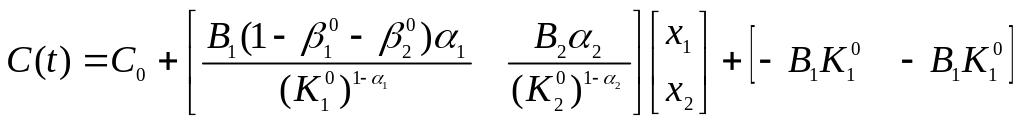
,(3.14)

где - значение потребления в стационарной точке.

Таким образом, имея уравнение (3.13), можно поставить задачу приведения системы в начальное стационарное состояние (где величины отклонений =0, i=1,2), если произошло некоторое отклонение от него.

Структурная схема полученного линейного объекта представлена на рис. 3.4, где ,

, ,

, ,

матрицы с постоянными коэффициентами.

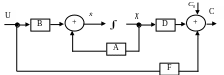
Рис. 3.4. Структурная схема линеаризованной модели двухсекторной

экономики

3.4. Решение и преобразование моделей систем

Анализируя рассмотренные примеры объектов различной природы, можно заметить, что мы пришли к абсолютно идентичным с математической точки зрения моделям.

Системы (3.1), (3.4) и (3.13) могут быть представлены в общем виде

, (3.15)

где x – вектор состояний длиной n, x ;

A – матрица коэффициентов размером [n n],

u – вектор управляющих (входных) воздействий длиной r, u ;

B – матрица коэффициентов размером [n r];

f – вектор внешних возмущающих воздействий длиной q, f ;

G – матрица коэффициентов [n q].

Представление системы дифференциальных уравнений первого порядка в виде (3.15) называется нормальной формой системы линейных дифференциальных уравнений.

Напомним некоторые факты из теории решения систем линейных дифференциальных уравнений. Для этого введем фундаментальную систему решений

, (3.16)

каждое из которых является вектором-столбцом

, , (3.17)

и решением однородного уравнения

, (3.18)

причем система решений (3.16) линейно независима.

Матрица , составленная из линейно независимых вектор-столбцов (3.17) называется фундаментальной матрицей системы (3.18), а детерминант матрицы называется детерминантом Вронского системы решений (3.16) и обозначается W(t). Для фундаментальной матрицы, в силу независимости решений (3.16), всегда выполняется условие

W(t) = det X(t) 0.

Если известна фундаментальная система решений (3.16) для системы (3.18), то решение для неоднородной системы линейных дифференциальных уравнений (3.15) будем искать в виде

x(t) = X(t)C(t), (3.19)

где С(t) – переменный произвольный вектор. Подставив (3.19) в (3.15) и учтя (3.18), получим

. (3.20)

Проинтегрировав (3.20) и подставив результат в (3.19), положив, что , и используя начальное условие , представим решение неоднородной системы (3.15) в виде

. (3.21)

Если B(t), u(t), G(t), f(t) интегрируемые функции, то решение (3.21) всегда существует, т.к. всегда существует и W(t) 0.

Однако не всегда модель объекта получается в виде нормальной системы (3.15). Зачастую описание объекта приводит к дифференциальному уравнению типа

, (3.22)

которое с помощью замен

и подстановкой их в (3.22) для отыскания можно привести к виду

+ u.(3.23)

В разделе 2 для передаточных функций мы получили общую форму передаточной функции динамической системы

, ,

которая соответствует уравнению системы

. (3.24)

В силу коммутативности дифференциальных операторов это уравнение можно представить в виде

, (3.25)

где p=d/dt.

Из (3.25) следует:

, (3.26)

. (3.27)

Введем замены

. (3.28)

С учетом (3.28) из (3.27) получим

(3.29)

а следовательно система (3.28) – (3.29) принимает нормальный вид

+ u, (3.30)

эквивалентный исходному уравнению (3.24).

3.5. Преобразование нормальных систем дифференциальных уравнений

При синтезе и анализе систем управления может возникнуть необходимость рассмотрения функционирования систем в новых, может быть, более удобных для анализа координатах. Рассмотрим возможность использования линейных преобразований координат в системах вида (3.15) с постоянными коэффициентами.

Функционирование системы опишем парой уравнений

(3.31)

где первое уравнение описывает эволюцию системы, а второе – изменение выходного (наблюдаемого) вектора.

Определим новый фазовый вектор с помощью невырожденного линейного преобразования T

. (3.32)

Из (3.32) можно найти исходный вектор

(3.33)

где, в силу невырожденности преобразования Т, обратное преобразование существует, и, подставляя (3.33) в (3.31), получим

или

(3.34)

Новое представление (3.34) эквивалентно первоначальной системе (3.31).

При моделировании динамических систем желательно получить в пределах принятого приближения как можно более простую модель. Для линейных моделей вида (3.15) используют канонические формы. Представление модели в канонической форме, например (3.23), как правило, делает ее более простой и обозримой, уменьшая число коэффициентов, входящих в модель, сокращает число связей между элементами. Правильный выбор канонической формы может привести к заметной экономии вычислительных ресурсов и улучшить такие характеристики вычислительного процесса, как точность, быстродействие, вычислительную устойчивость и т.п.

Существует достаточно большое количество канонических форм и методов перехода к ним. Нам нет надобности углубляться в эти проблемы, а познакомиться с ними можно в специальной литературе, приведенной в конце книги [10, 20, 21, 22].

Большую озабоченность может вызвать тот факт, что в большинстве случаев системы описываются нелинейными дифференциальными уравнениями, которые в векторном виде можно записать, если допустимо решение относительно производных:

, (3.35)

где , – векторы, а – вектор-функция, у которой .

Тогда, если существуют и непрерывны по всем переменным частные производные вектор-функции F, в окрестности некоторой точки ( ) правая часть уравнения (3.35) может быть разложена в ряд Тейлора до линейных членов:

,(3.36)

где , ,

, , .

С учетом равенства (3.35), которое выполняется, и в точке ( ) уравнение (3.36) в силу малости и приобретает линейный вид:

. (3.37)

Следует заметить, что процесс линеаризации позволяет получить простую модель, для которой, как мы увидим далее, разработаны эффективные методы решения задачи синтеза управления. Однако упрощение модели может привести к потере принципиально важных свойств системы, которыми обычно обладают нелинейные системы. Поэтому вопрос о необходимости линеаризации должен решаться аналитиком-исследователем. Обычно сначала решается линеаризованная задача, а затем более сложная задача нелинейного анализа системы и синтеза управления.