Приклад

Знайти найбiльше й найменше значення функцiї

z = x² + 2y ²- 2x - 8y + 4 в замкненому трикутнику АОВ, обмеженому осями координат i прямою х + у – 4 = 0 (рис.3).

Розв’язання

Знайдемо частинні похідні:

Прирівнявши частинні похiднi до нуля i розв'язавши одержану систему

,

знаходимо стацiонарну точку Р₀(1;2). Ця точка належить заданiй областi.

Обчислимо значення функції в цій точці:

z(P₀) = z(1;2) = 1 + 8 – 2 – 16 + 4 = -5.

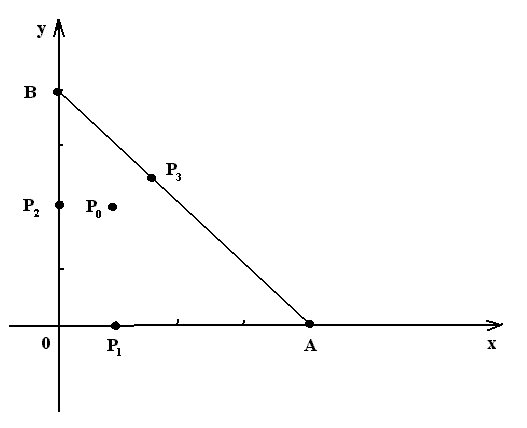
Рис.3

Межа області складається з вiдрiзка ОА осi Ох, вiдрiзка ОВ осi Оу i вiдрiзка АВ. Знайдемо найбільше і найменше значення функції z на кожному з цих трьох вiдрiзкiв.

На відрізку ОА y = 0, . Якщо у = 0, то z(x) = x² - 2x + 4.

- стаціонарна точка на відрізку ОА;

Обчислимо значення функцiї на кiнцях вiдрiзка ОА, тобто в точках О(0;0) i А(4;0):z(0;0) = 4, z(4;0) = 12.

На вiдрiзку ОВ х = 0, . Якщо х = 0, то z(y) = 2y² - 8y + 4.

Р₂(0;2) - стаціонарна точка на відрізку ОВ; z(P₂) = -4.

В точцi О(0;0) значення функцiї вже було знайдено. Обчислимо значення функції в точці В: z(B) = z(0;4) = 4.

Тепер дослідимо функцію на вiдрiзку АВ. Рівнянням прямої АВ буде у = 4 – х. Підставивши цей вираз для у в задану функцію z, одержимо z = x² + 2(4 - x)² - 2x - 8(4 - x) + 4 = 3x² - 10x + 4, 0 x 4. Далі дістанемо

звідки х = 5/3. Оскільки у = 4 - х, то у = 7/3.Р₃(5/3;7/3) - стаціонарна точка на вiдрiзку АВ. Обчислимо значення функції в цій точці z(P₃) = z(5/3;7/3) = -13/3.

Значення функції на кінцях вiдрiзка АВ знайденi ранiше.

Порівнюючи одержанi значення функцiї z в стацiонарній точцi Р₀ заданої областi, в стацiонарних точках на межi областi Р₁, Р₂, Р₃ i в точках О, А, В, робимо висновок, що найбiльше значення в заданiй замкненiй областi функцiя z має в точцi А, найменше значення - в точцi Р₀(1;2).

Отже, z_найб = z(4;0) = 12; z_найм = z(1;2) = -5.

Умовний екстремум

Нехай потрібно знайти екстремум функції при умові, що на нелалежні змінні x і y накладені додаткові обмеження: . Геометрично це означає, що точка лежить на лінії, визначеній рівнянням . Якщо його можна розв’язати відносно y, тобто задати лінію явним рівнянням , то розв’язання зведеться до дослідження на екстремум функції однієї змінної .

З необхідної умови екстремуму функції однієї змінної маємо , що в термінах функції f дає

. (1)

Перетворимо умову (1) введенням функції . Для цього продиференціюємо рівняння , вважаючи у ньому y як неявну функцію x:

. (2)

Помножимо рівність (2) на число , яке підберемо потім, і додамо одержану рівність до рівності (1). Одержимо:

. (3)

Число підберемо так, щоб

.

Тоді з рівності (3) одержимо, що

.

Таким чином, критичні точки функції визначаються з системи рівнянь

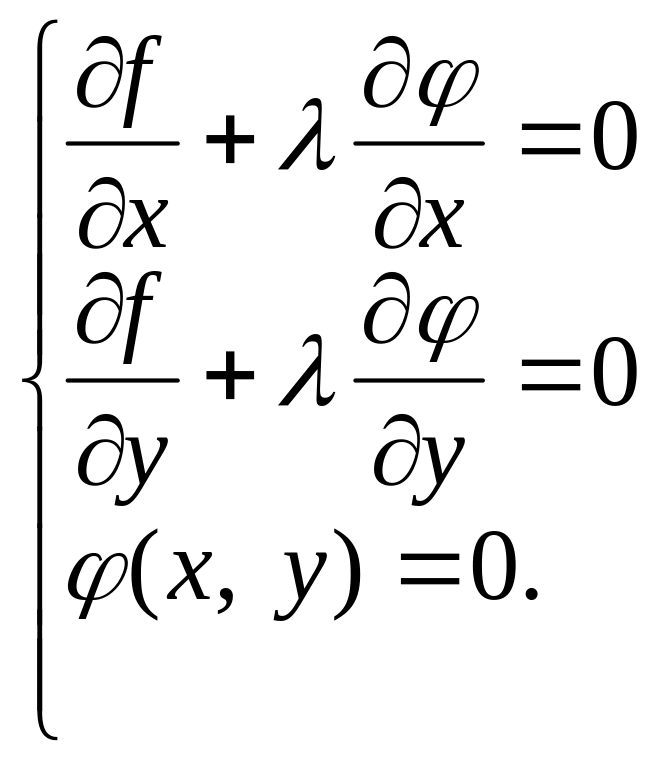(4)

Систему рівнянь (4) можна записати інакше, ввівши так звану функцію Лагранжа . Тоді система набуває вигляду

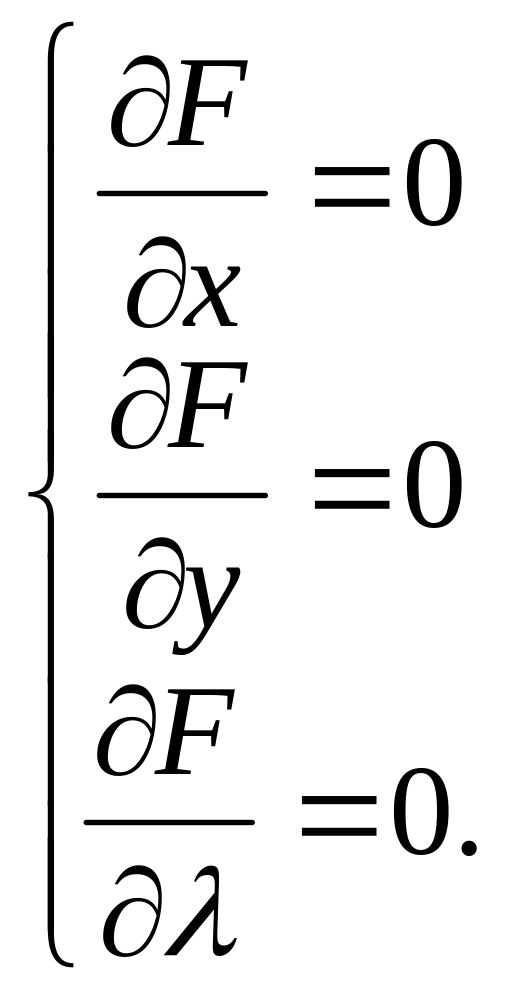(5)

Розв’язавши систему рівнянь (5), отримаємо критичні точки функції . Питання про існування екстремуму у критичних точках вирішується окремо, зокрема, з фізичних або геометричних міркувань.

Для функції з двома рівняннями зв’язку і функція Лагранжа має вигляд

а система (5) записується так:

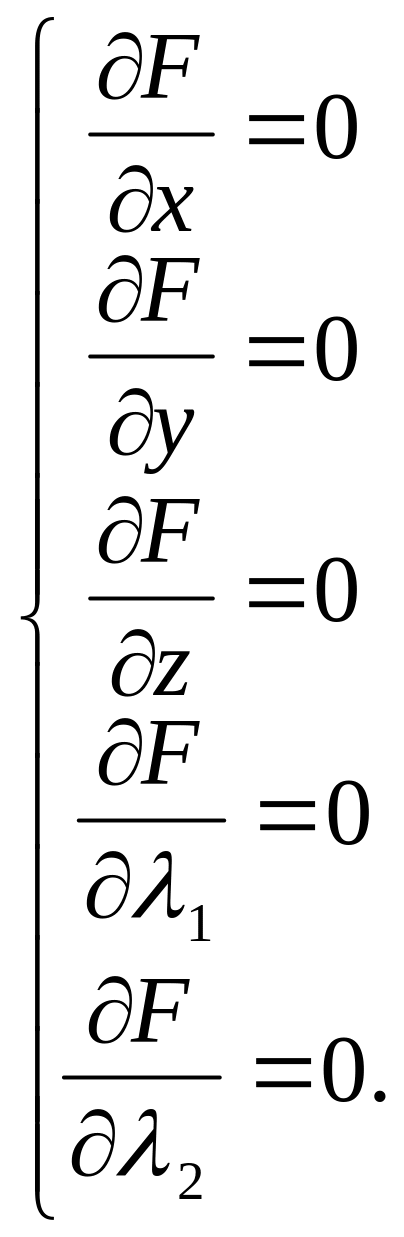(6)