Частинні похідні функції двох незалежних змінних

Нехай задані функція z = f(x,y) і точка (х,у) D. Якщо зміна функції z відбувається при зміні тільки одного з аргументів, наприклад х, при фіксованому значенні другого аргументу у, то функція набуває приросту , який називається частинним приростом функції f(x,y) пo аргументу x.

Означення. Якщо існує скінченна границя

то вона називається частинною похідною функції f(x,y) по аргументу х і позначається одним із символів

f'_x(x, y), тобто

Аналогічно дається означення частинного приросту z по у і частинної похідної f(x,y) пo y:

При обчисленні частинних похідних користуються вже відомими правилами і формулами диференціювання функції однієї змінної, вважаючи при цьому другу змінну сталою.

Приклад. Знайти частинні похідні функції

Маємо: = ( фіксоване ); ( фіксоване ).

Приклад. Знайти частинні похідні функції z = arctg .

=

= ;

.

Аналогічно даються поняття частинних похiдних функцій трьох і більше змінних.

Частинні похідні функції кількох змінних визначаються і обчислюються також в припущенні, що змінюється тільки одна з незалежних змінних, а інші при цьому фіксовані.

Частинна похідна функції кількох змінних має той же механічний зміст, що і похідна функції однієї змінної, це швидкість зміни функції відносно зміни одного з аргументів.

Повний диференціал функції z = f(x,y)

Означення. Повним приростом функції z = f(x,y) в точці (х,у) називається різниця де і довільні прирости аргументів.

Означення. Функція називається диференційовною в точці , якщо її повний приріст можна подати у вигляді

(3)

де .

Теорема (достатні умови диференційовності). Якщо функція має неперервні частинні похідні в точці , то вона диференційовна в цій точці.

Означення. Повним диференціалом функції z = f(x,y) називається головна частина повного приросту лінійна відносно приростів аргументів і , тобто

Диференціали незалежних змінних співпадають з їх приростами, тобто

.

Повний диференціал функції z = f(x,y) обчислюється за формулою:

Аналогічно, повний диференціал функції трьох змінних u = f(x,y,z) обчислюється за формулою:

Приклад. Знайти повний диференціал функції z = ln(x²+y).

Оскільки ,

тоді

Застосування диференціала у наближених обчисленнях

Розглянемо функцію . Знайдемо повний приріст цієї функції:

,

оскільки за формулою (3)

,

тоді

,

яка в розгорнутому вигляді записується так:

. (4)

Цією наближеною рівністю зручно користуватися, коли та легко обчислюються в точці . Наближена рівність (4) тим точніша, чим менші прирости і .

Приклад. Обчислити

Частинні похiднi вищих порядкiв.

Для введення цих понять використаємо конкретний приклад функції . Її частинні похідні

знову є функціями двох змінних, від яких можна, в свою чергу, обчислювати частинні похідні:

Одержали чотири частинні похідні, які називають частинними похідними другого порядку функції .

У наведеному прикладі

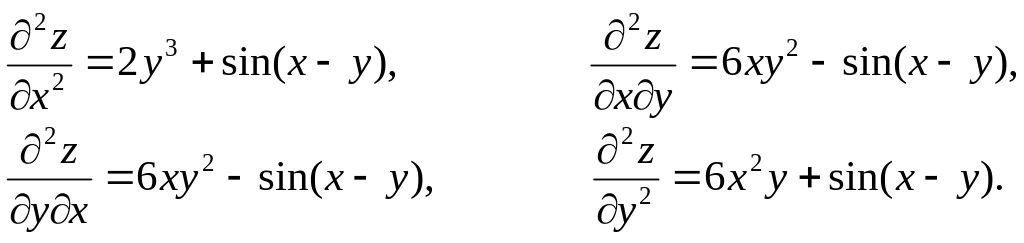
Знову одержали функції двох змінних, від яких, у свою чергу, можна обчислювати частинні похідні. По відношенню до функції їх називають частинними похідними третього порядку:

і т.д.

У прикладі звертає на себе увагу рівність , яка показує, що результат не залежить від порядку диференціювання. Частинні похідні називають змішаними. Виявляється, що (за умови їх неперервності) вони рівні, тобто результат не залежить від порядку диференціювання:

(5)

У випадку розривності змішанних частинних похідних рівності (5) можуть і не мати місця.