Диференціали вищих порядків

нехай функція має в деякій області D площини неперервні частинні похідні до - го порядку включно, . Зафіксуємо прирости і і запишемо диференціал першого порядку

,

який є функцією двох змінних. Тому можна говорити про диференціал цієї функції d(dz(x, y)), який називають диферен-ціалом другого порядку функції , і позначають , або коротше :

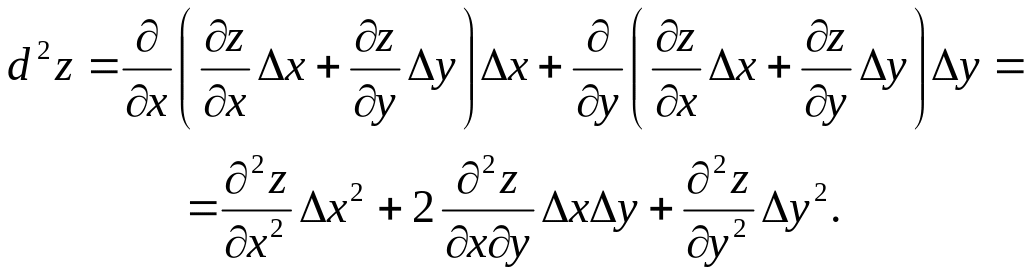
При обчисленні використали рівність змішаних частинних похідних.

Диференціал другого порядку знову є функцією двох змінних і можна говорити про диференціал цієї функції, який називають диференціалом третього порядку функції і позначають або коротше . Обчислення приводить до рівності

яка нагадує куб суми.

Якщо уже визначений, то за означенням

.

Методом повної математичної індукції можна показати справедливість наступної символічної формули для диференціала n - го порядку:

. (6)

Формулою (6) користуються так: треба формально записати праву частину за формулою бінома Ньютона

,

а потім до приставити літеру z:

Наприклад,

Екстремум функції двох змінних

Означення. Функція має в точці локальний максимум (мінімум), якщо існує окіл точки , у якому для кожної точки виконується нерівність , тобто приріст зберігає знак у деякому околі точки (рис. 1. і рис. 2).

Т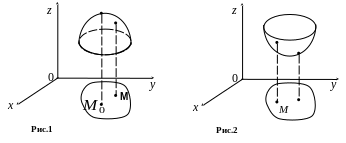 еорема (необхідні умови екстремуму). Нехай - точка локального екстремуму функції . Якщо існують частинні похідні і , то вони дорівнюють нулю.

Доведення. Розглянемо випадок локального максимуму. Тоді у деякому околі точки приріст і, отже,

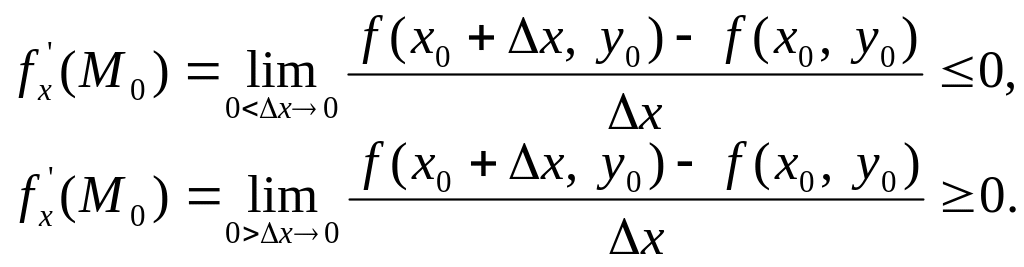
Звідси випливає, що Аналогічно доводиться, що . Теорему доведено.

Означення . Точка , у якій частинні похідні і дорівнюють нулю або не існують, називається критичною (або стаціонарною) точкою функції .

Нехай М₀(х₀,у₀) - стаціонарна точка функції z = f(x,y). Позначимо

і покладемо ∆ = =

Тоді справедлива теорема (достатні умови екстремуму): якщо ∆>0, то функція має в точці М₀ екстремум, а саме максимум при А<0 і мiнiмум при А>0 ; якщо ∆<0, то в точці М₀ екстремуму немає; якщо ∆ = 0, то запитання про існування екстремуму залишається відкритим.

Приклад. Знайти екстремум функції z = x² – xy + y² + 9х - 6у + 20.

Знаходимо частиннi похiднi першого порядку:

Скористувавшись необхідними умовами екстремуму, знаходимо стацiонарнi точки:

Одержали одну стаціонарну точку М(-4;1)

Знаходимо частинні похідні другого порядку і їх значення в знайденій стаціонарній точці:

Зрозуміло, що частинні похідні другого порядку постійні в будь - якій точці, зокрема, в точці М(-4;1). Маємо: А = 2, В = -1, С = 2; ∆ = AC – B² = 4 – 1 = =3 > 0; A > 0.

Отже, в точці М(-4;1) задана функція має мiнiмум.

Знайдемо значення функції в цiй точцi:

z_min = z(-4;1) = (-4)² - (-4)·1 + 1² + 9·(-4) - 6·1 + 20 = -1.

Найбільше та найменше значення функції в замкненій області

Функція , диференційовна в обмеженій області, набуває в ній найбільшого та найменшого значень в стаціонарних точках або в граничних точках. Таким чином, щоб знайти найбiльше і найменше значення функцiї в замкненій областi, треба:

1) знайти стацiонарнi точки, розмiщенi в данiй областi, i обчислити значення функцiї в цих точках;

2) дослідити функцію на екстремум на межі області;

3) з усix найдених значень вибрати найбiльше i найменше.