Розділ V Функції багатьох змінних

Функція двох незалежних змінних, основні означення

Частинні похідні функції z=f(x;y).

При вивченні багатьох закономірностей доводиться зустрічатися з функціями від двох (і більше) незалежних змінних. Наприклад, площа S трикутника із стороною х і висотою у є функція двох змінних: S = f(x,y) (S = 1/2xy).

Якщо розглянути прямокутний паралелепіпед з ребрами х,у,z, то його об'єм є функція трьох змінних: V = f(x, y, z) (V = xyz).

Функції багатьох змінних можна виявити в сфері економіки, військової справи та взагалі в природі. Наприклад, процес гідравлічного переміщення, викликаний дощами, таненням снігів або меліорацією, дуже залежить від рельєфу місцевості, гідрогеологічних умов, сільськогосподарської діяльності і погоди.

Основні означення, які відносяться до функції кількох змінних, є узагальненням відповідних означень для функції однієї змінної. Зупинимося на функції двох змінних.

Означення. Змінна величина z називається функцією двох незалежних змінних х та у , якщо кожній парі значень х,у із множини D ставиться у відповідність одне визначене значення z із множини Е: z = f(x,y).

Означення. Множина D називається областю визначення функції z, а множина  – множиною її значень. Змінні х,у по відношенню до функції z називаються її аргументами.

Для функції можна говорити про її графік. Якщо у просторі зафіксована прямокутна декартова система координат і - область існування функції , то її графіком вважають множину M точок цього простору з координатами x, y, . Наприклад, графіком функції є параболоїд обертання. графіком функції є верхня напівсфера.

Про графік функції трьох і більшого числа змінних у звичайному розумінні говорити вже неможливо. Такі функції можна вивчати за допомогою поверхонь рівня, а функції двох змінних – за допомогою ліній рівня.

Означення. Лінією рівня функції називають лінію у площині XOY, задану рівнянням .

Приклад . Знайти область визначення функції:

,

Поняття границі та неперервності функції z = f(x,y) в точці вводяться аналогічно цим поняттям для функції однієї змінної.

Означення. Дійсне число A називається границею функції у точці , якщо для довільного числа існує таке число , що для всіх точок , відмінних від точки , і таких, що віддаль , виконується нерівність .

Це записують одним із двох способів:

.

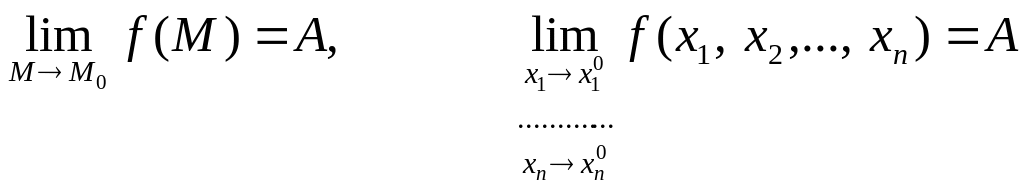Означення. Функція називається неперервною в точці , якщо .

Зокрема, для функції двох змінних означення неперервності в точці записується так:

(1)

Якщо позначити різниці

,

то рівність (1) матиме вигляд

(2)

тобто неперервність функції у точці означає, що нескінченно малим приростам і аргументів x і y відповідає нескінченно малий приріст функції .

Якщо рівність (1) не має місця, то функцію називають розривною в точці . Множина точок розриву функції може утворювати лінію. Наприклад, функція розривна в кожній точці прямої , оскільки вона не визначена в кожній точці цієї прямої.