
- •20. Некоторые основные св-ва интеграла от функции комплексной переменной:
- •21. Производная фкп. Условия Коши-Римана.
- •23. Ряды Тейлора и Лорана.
- •24. Геометрический смысл модуля и аргумента аналитической функции.
- •25. Вычеты.
- •28. Оригиналы и изображения.
- •35. Решение систем дифференциальных уравнений.
- •22. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.
- •6. Замена переменных в 3-ом интегр. Цилиндрич и сферические координаты
- •7. Приложение 3-ых интегралов
- •8. Криволинейный интеграл 1 рода, опр. ,
- •9. Криволинейный интегр 2-ого рода, опр., св-ва и вычисление
- •10. Формула Остроградского-Грина.
- •11. Условие независимости криволинейного инт. 2-го рода от пути интегр.
- •13 Пов. Инт. 1-го рода.Его св. И выч.
- •14 Пов инт 2-го рода
- •17Формула Остроградского-Гаусса
- •16 Векторное поле. Поток векторного поля.
- •18 Циркуляция поля.
7. Приложение 3-ых интегралов
а)объем
тела:![]()
б)масса тела:![]()
γ(x,y,z)-поверхностная плотность
в)статистические моменты:
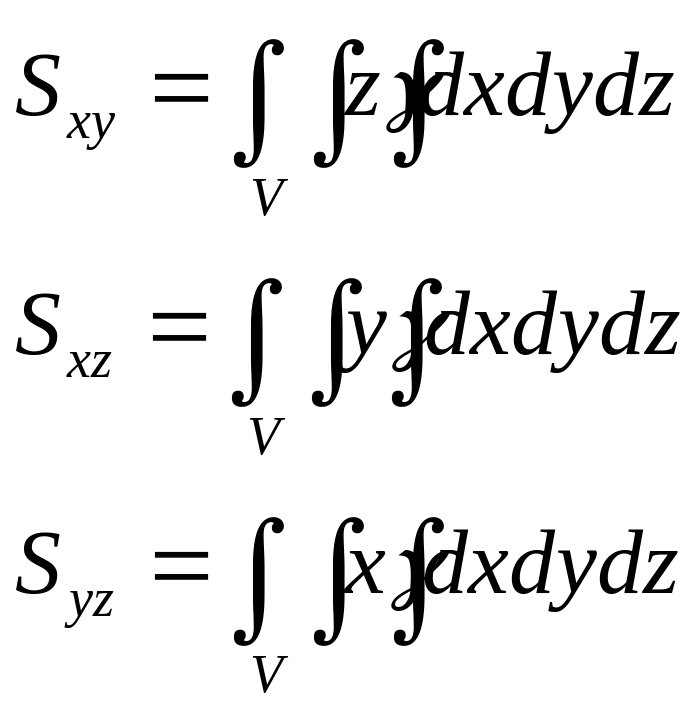
г)центр тяжести тела
![]()
8. Криволинейный интеграл 1 рода, опр. ,
св-ва и вычисление:
![]()
Св-ва криволин интегр 1 рода:
1.
![]()
2.
![]()
3.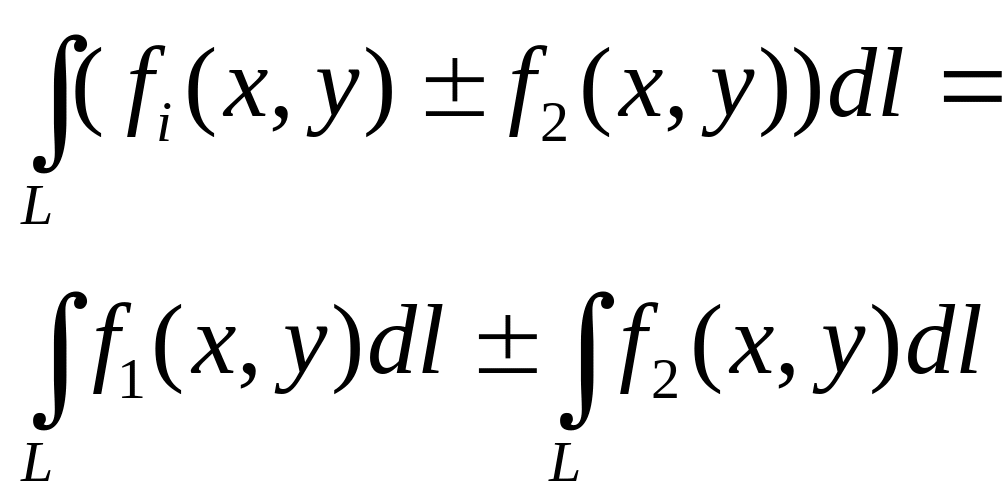
4.

5.
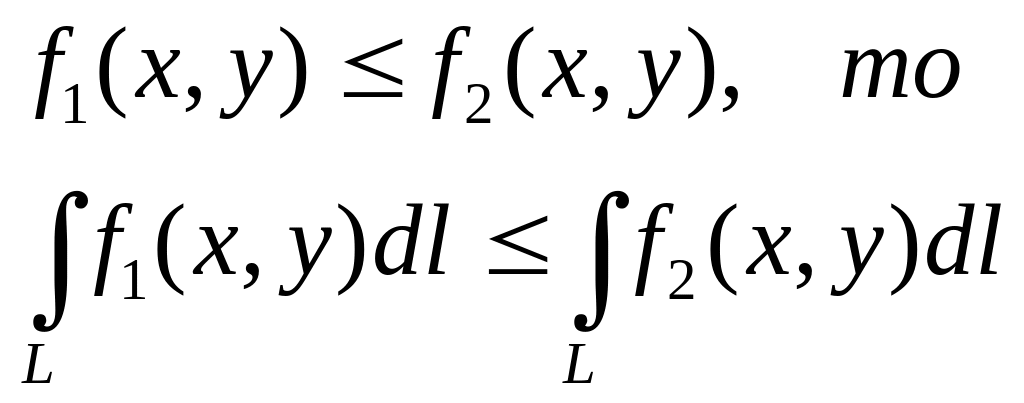
6.
![]()
7.
![]()
Вычисление кривол интегр 1-ого рода
а) параметрическое представление
![]()
б) явное представление:
![]()
в) полярное представление:
![]()
9. Криволинейный интегр 2-ого рода, опр., св-ва и вычисление
Если кривая АВ гладкая , а ф-ция P(x,y) Q(x,y) непрерывны на прямой АВб то криволинейный интеграл 2-ого рода существует
Св-ва кр. интегр. 2-ого рода
1.![]()
2.
![]()
3.
![]()
Если АВ лежит в плоскости ┴ оси ОХ
4. Криволинейные интегр по замкнутой кривой не зависит от выбора начальной точки
Вычисление криволин интегр 2-ого рода
а)параметрическое представление
![]()
б)явное представление
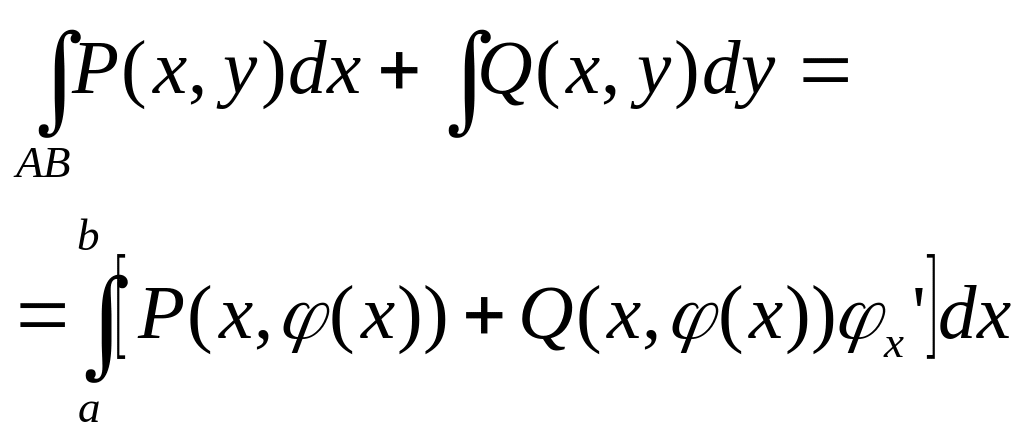
12 Прил кривол лин инт 1-го рода
1) длина плоской
кривой АВ
![]() 2)
Площ цилиндрической пов. Если направлением
цил пов служит кривая АВ прин oxy
, обр пораллельной oz
, то пл пов задаваемой ф z=f(xy)
=
2)
Площ цилиндрической пов. Если направлением
цил пов служит кривая АВ прин oxy
, обр пораллельной oz
, то пл пов задаваемой ф z=f(xy)
=![]() 3)
Масса кривой
3)
Масса кривой
![]() 4) Статический момент и центр тяжести.
Статистический момент относительно ox
и oy
материальной кривой АВ равны
4) Статический момент и центр тяжести.
Статистический момент относительно ox
и oy
материальной кривой АВ равны
![]()
![]()
![]()
![]()
2-го рода6 1) площадь
плоской фигуры расположенной в плоскости
oxy
и ограниченной замкнутой кривой можно
найти
![]() 2)
Работа переменной силы Переменная сила
F(P(xy),Q(xy))
на криволинейном участке АВ производит
работу
2)
Работа переменной силы Переменная сила
F(P(xy),Q(xy))
на криволинейном участке АВ производит
работу
![]()
10. Формула Остроградского-Грина.
Связь между дв. Инт. По области Д и криволин. Инт. По области L устанавливают формулу Остроградского-Грина.
Пусть на плоскости OXY задана область Д огр. Кривой пересекающееся с прямыми параллельными корд. Осям не более чем в 2 точках, т. е. область Д правильная.
Т1.Если ф. P(x,y),
Q(x,y)
непрерывно вместе со своими чанными
производными
![]() ,
,
![]() области
Д то справедлива форм.
области
Д то справедлива форм.![]() (ф.Остр.-Гр.)
(ф.Остр.-Гр.)
, L граница области Д и интегрирование вдоль кривой L производится в положительном направлении.До- во.
Т2.Если = (2), то подинтегр. Выражение P*dx+Q*dy явл. Полным диф. Функции U=U(x,y).
P*dx+Q*dy =U(x.y)
Удовлетворяет
условию (2) можно найти используя ф.
![]()
Зам.1 Чтобы не спутать переменную интегр. X с верхним преднлом ее обозн. Другой буквой.
Зам. 2 в качестве нач точки(x0,Y0) обычно берут точку (0.0)
11. Условие независимости криволинейного инт. 2-го рода от пути интегр.
Пусть т. А (X1,
Y1),
В(X2,
Y2),.
Пусть произв. точки области Д. Точки А
и B
можно соеденить различными линиями. По
каждой из них кр. Инт.
![]() будет
иметь свое значение если же значение
по всем кривым одинаково, то интеграл
не зависит, от вида пути инт., в этам сл
достаточно отметить первонач. Точку А
(X1,
Y1)
и конечную В(X2,
Y2).
будет
иметь свое значение если же значение
по всем кривым одинаково, то интеграл
не зависит, от вида пути инт., в этам сл
достаточно отметить первонач. Точку А
(X1,
Y1)
и конечную В(X2,
Y2).
Т. Для того, чтобы кр. Инт.
Не зависит от пути
инт. Области Д в кот. Ф. P(X,Y),
Q(X,Y)
непрерывны вместе со своими производными
и необходимо, чтобы в каждой точке
области
![]() =
Док-во
=
Док-во
Кр. Инт. 2-го рода не зависит отпути интегрирования
Зам.
=
отсюда
получаем, что
![]()
