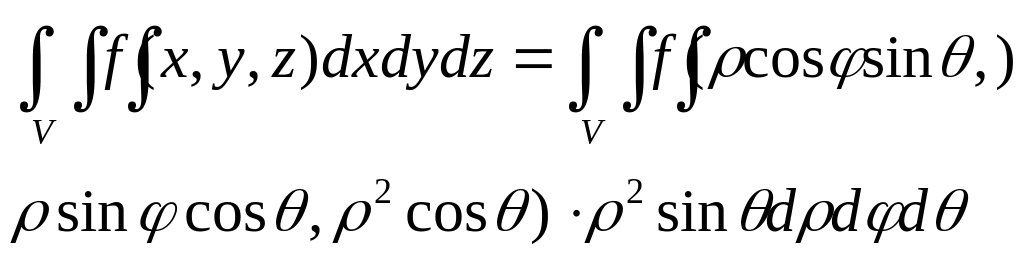22. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.

Степенным рядом называется функциональный ряд вида , где - постоянные числа, называемые коэффициентами ряда.

Теорема Абеля.

Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком х, для которого .

Если ряд расходится при некотором значении , то он расходится при всяком х, для которого .

Доказательство: Так как по предположению числовой ряд сходится, то его общий член при , а это значит, что существует такое положительное число М, что все члены ряда по абсолютной величине меньше М. Перепишем ряд в виде и рассмотрим ряд из абсолютных величин его членов:

Члены этого ряда меньше соответствующих членов ряда

При последний ряд представляет собой геометрическую прогрессию со знаменателем и, следовательно, сходится.

Теперь нетрудно доказать и вторую часть теоремы: пусть в некоторой точке ряд расходится. Тогда он будет расходиться в любой точке х, удовлетворяющей условию . Действительно, если бы в какой-либо точке х-, удовлетворяющей этому условию, ряд сходился, то в силу только что доказанной первой части теоремы он должен был бы сходиться и в точке , так как . Но это противоречит условию, что в точке ряд расходится. Следовательно, ряд расходится и в точке х. Теорема полностью доказана.

Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.

1. Двойной интеграл его опр. и св-ва:

Двойным интегр. от ф-ции f(x,y) по обл. D наз. предел, к которому стремится n-я интегр. сумма

при стремлении к 0 наибольшего диаметра частичных обл..

Св-ва: 1.

2.

3.

4. если f(x,y)>=0 ,то

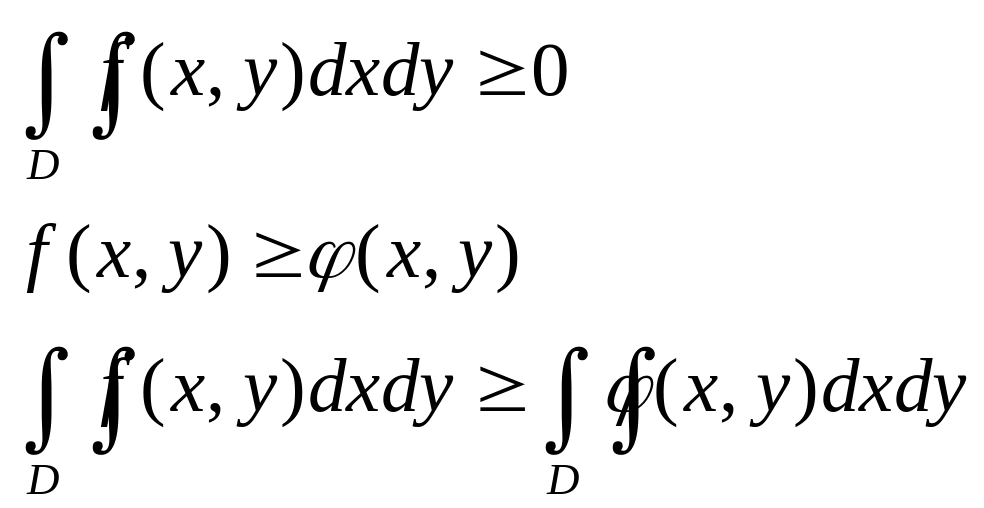
5.

где S –площадь обл. D

6.

2. Вычисление двойного интеграла

Для вычисления дв. интегр применяется следующая ф-ла:

где S(х)-площю сечения плоскости ┴0х

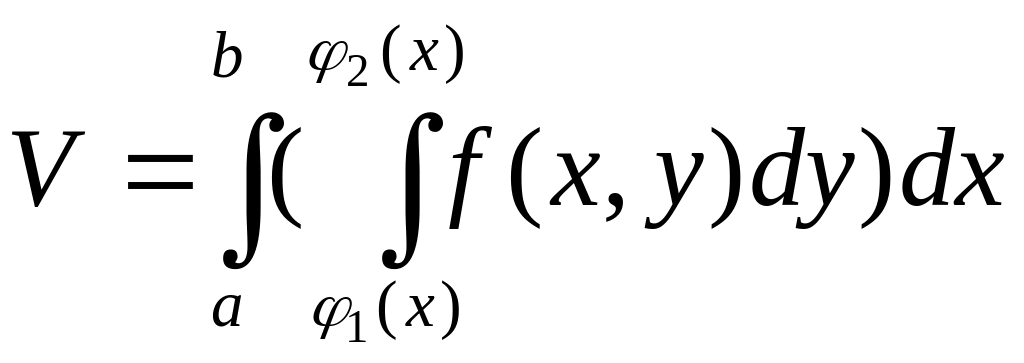
Замена переменных в двойн интегр . Якобиан.

3 Двойн интегр в полярных координатах

Введем замену переменных в 2-ом интегр х=φ(u,v)

Y= φ(u,v) если эти ф-ции лежат в обл. D

D<=0UV –непрерывн частные производные 1-ого порядка

и определитель

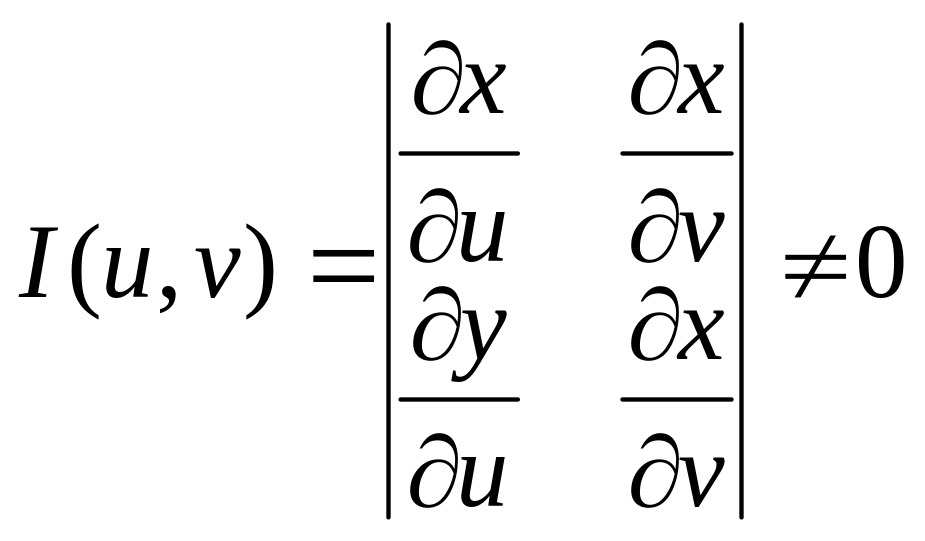
Замена полярных коорд. X=rcosφ Y=rsinφ –непрер. Диф ф-ции

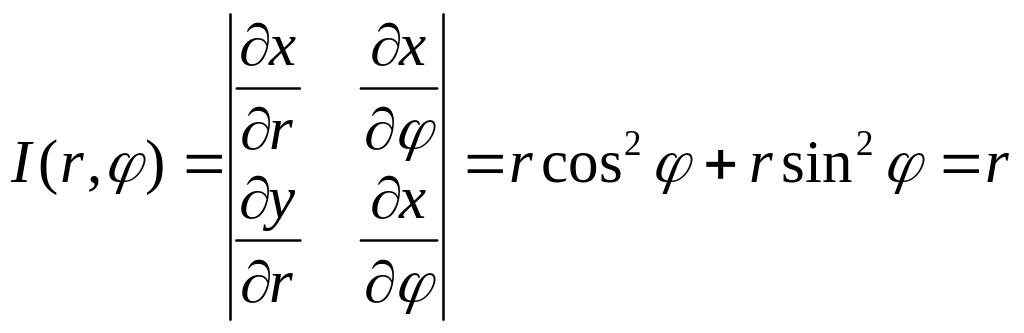
4. Приложения 2-ых интегралов

а) объем тела

б) площадь плоской фигуры

в)масса плоской фигуры

г)Статические моменты и центр тяжести плоской

5. 3-ой интеграл, его св-ва и вычисление

3-ой интегр равен произедению значения подынтегр ф-ции в некоторой точке области интегрирования на объем област интегр.

Св-ва 3-ого интеграла:

1.

2.

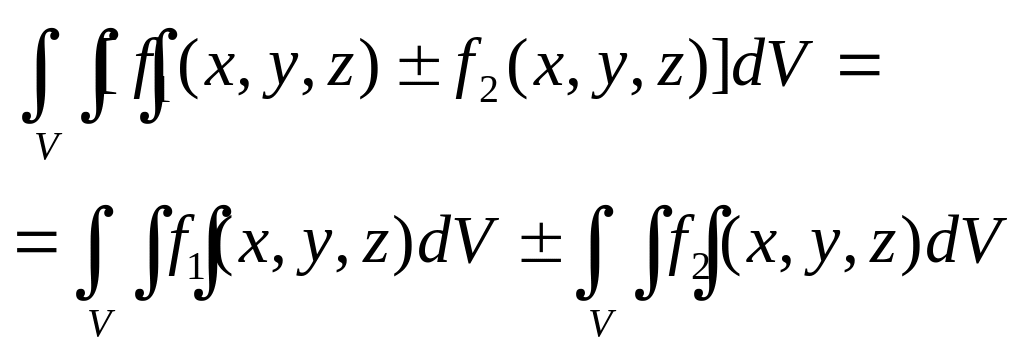
3. 4.

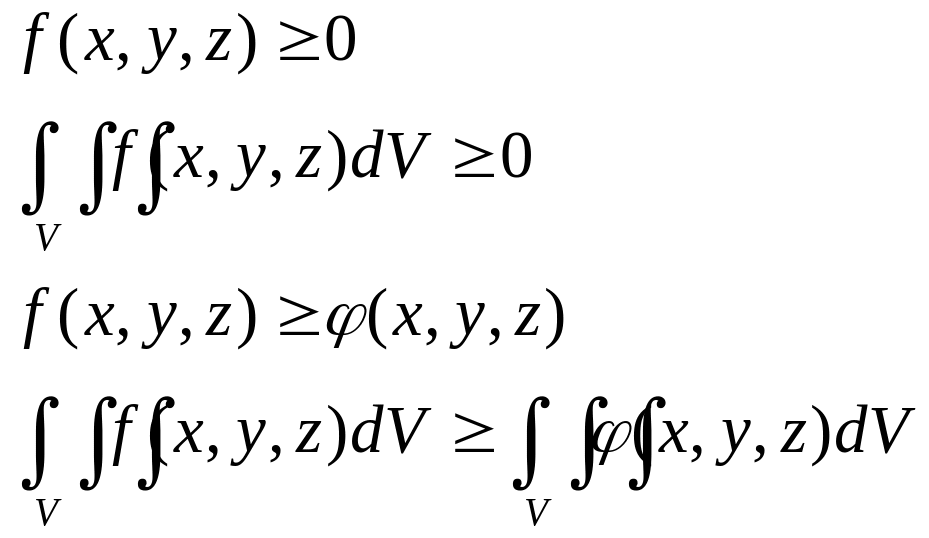
5.

6.

7.

6. Замена переменных в 3-ом интегр. Цилиндрич и сферические координаты

Пусть: х=φ(u,v,w); Y= ψ(u,v,w); Z=λ(u,v,w)

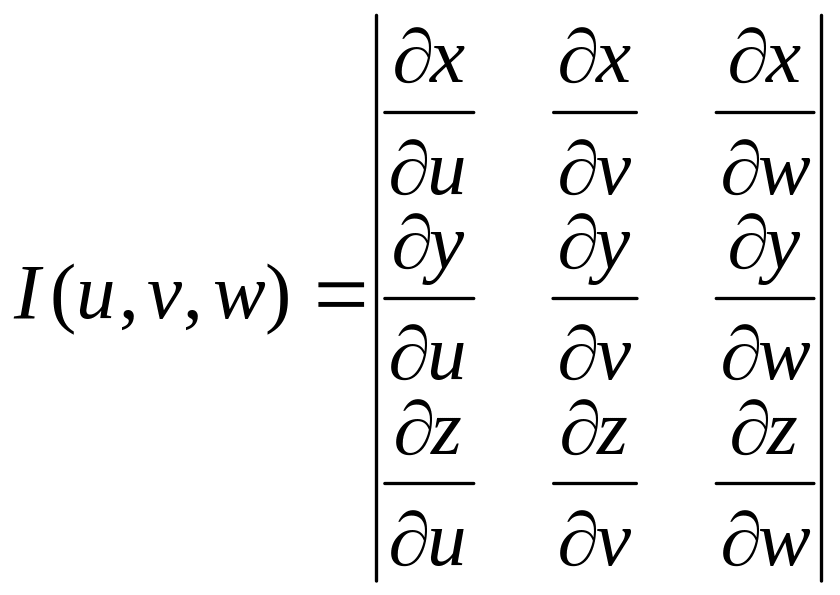
То справедлива ф-ла замены

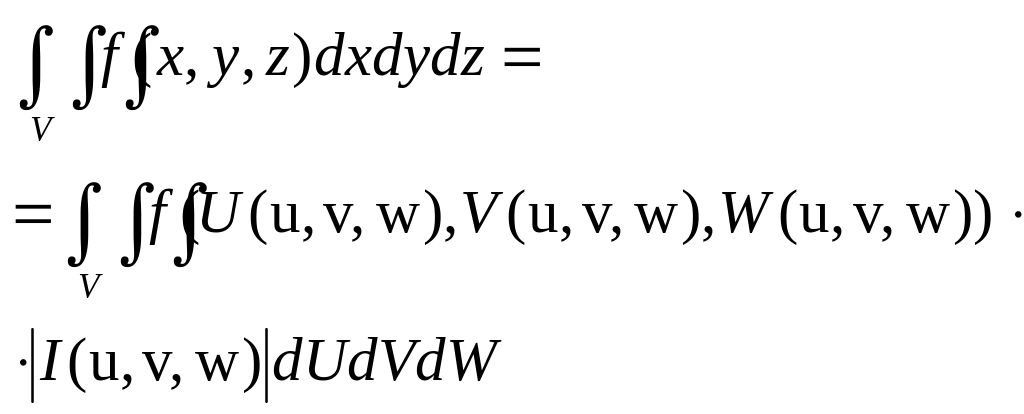
Цилиндрические координаты:

Положение точки в пространстве OXYZ можно определить заданием 3-х чисел r, φ,z (цилиндрические координаты точки)

Заменяем x=rcos φ y=rsin φ z=z

Соответственно якобиан будет =r

Ф-ла замены

Сферические координаты:

x=ρcosφsinӨ y=ρsinφcosӨ z=ρcosӨ

ρ>=0; 0<=φ<=2π; 0<=Ө<= π

I(ρ, φ, Ө)= ρ²sin Ө

Ф-ла замены