
- •20. Некоторые основные св-ва интеграла от функции комплексной переменной:
- •21. Производная фкп. Условия Коши-Римана.
- •23. Ряды Тейлора и Лорана.
- •24. Геометрический смысл модуля и аргумента аналитической функции.
- •25. Вычеты.
- •28. Оригиналы и изображения.
- •35. Решение систем дифференциальных уравнений.
- •22. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости.
- •6. Замена переменных в 3-ом интегр. Цилиндрич и сферические координаты
- •7. Приложение 3-ых интегралов
- •8. Криволинейный интеграл 1 рода, опр. ,
- •9. Криволинейный интегр 2-ого рода, опр., св-ва и вычисление
- •10. Формула Остроградского-Грина.
- •11. Условие независимости криволинейного инт. 2-го рода от пути интегр.
- •13 Пов. Инт. 1-го рода.Его св. И выч.
- •14 Пов инт 2-го рода
- •17Формула Остроградского-Гаусса
- •16 Векторное поле. Поток векторного поля.
- •18 Циркуляция поля.
20. Некоторые основные св-ва интеграла от функции комплексной переменной:
Линейность:
![]()
Это св-во обобщается на любое конечное число функций.
При изменении ориентации кривой, по которой берется интеграл, на противоположную, знак интеграла изменяется на противоположный:
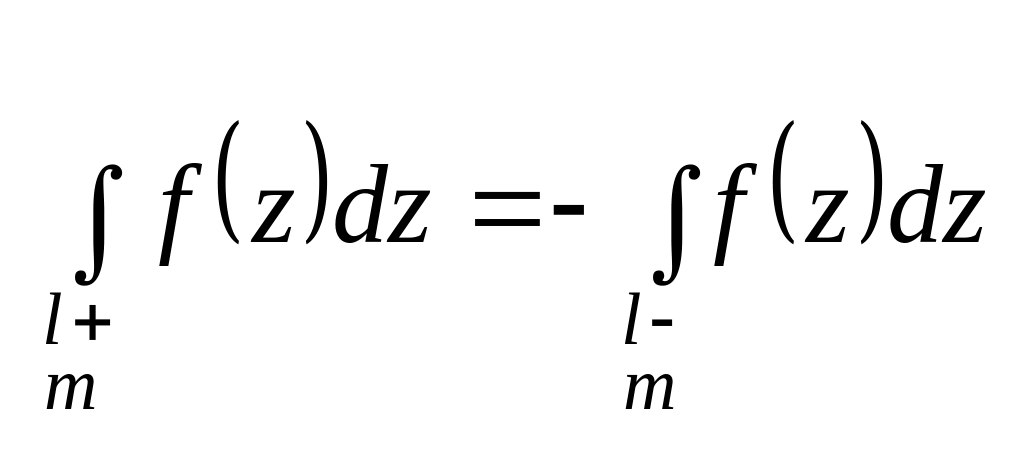 .
.
Модуль интеграла:
![]() .
.
21. Производная фкп. Условия Коши-Римана.
Производной однозначной ФКП
![]() называется предел отношения
называется предел отношения
![]() ,
если
,
если
![]() любым способом стремится к нулю.
любым способом стремится к нулю.
![]() .
.
Функция, имеющая производную при данном
значении
![]() ,
называется дифференцируемой при этом
значении
.
,
называется дифференцируемой при этом
значении
.
Если функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
то в этой точке существуют частные
производные
,
то в этой точке существуют частные
производные
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
причем эти производные связаны условиями:
,
причем эти производные связаны условиями:
![]() ,
,
![]() ,
которые называются условиями Коши-Римана.
,
которые называются условиями Коши-Римана.
Условия Коши-Римана являются необходимыми условиями дифференцируемости функции в точке .
Обратно, если частные производные , , , непрерывны в точке и условия Коши-Римана , выполнены, то функция дифференцируема в точке .
Производная функции
![]() выражается через частные производные
функций
выражается через частные производные
функций
![]() и
и
![]() по формулам:
по формулам:
![]()
23. Ряды Тейлора и Лорана.
Ряд Лорана по степеням
![]() - это формула вида
- это формула вида

Правильная часть ряда Лорана сходится
в круге
![]()
Главная часть ряда Лорана сходится в
круге
![]() ,
где
,
где
![]() - внешность круга.
- внешность круга.
![]() .
Если выполняется это условие, то ряд
Лорана сходится в кольце
.
Если выполняется это условие, то ряд
Лорана сходится в кольце
![]() .
.
Теорема Тейлора. Пусть функция
является аналитической в точке
![]() .
Следовательно,
.
Следовательно,
![]() ,
где
,
где
![]() - ряд Тейлора по степеням
.
Полученное разложение функции однозначно.
- ряд Тейлора по степеням
.
Полученное разложение функции однозначно.
Доказательство.
Теорема Лорана. Пусть функция
является аналитической в кольце
.
Тогда
![]() ,
где
- ряд Тейлора по степеням
.
Полученное разложение функции однозначно.
,
где
- ряд Тейлора по степеням
.
Полученное разложение функции однозначно.
24. Геометрический смысл модуля и аргумента аналитической функции.
По определению
![]() .
Пусть
.
Пусть
![]() .
.
![]() (1)
(1)
![]() (2)
(2)
Р ассмотрим
(1)
ассмотрим
(1)
![]() - вектор
- вектор
![]() .
.
![]() - его длина.
- его длина.
![]() - вектор
- вектор
![]() .
.
![]() - его длина.
- его длина.
![]() - коэффициент линейного растяжения
вектора при отображении
- коэффициент линейного растяжения
вектора при отображении
![]()
![]() - коэффициент деформации бесконечно
малого вектора, исходящего из
при отображении
.
- коэффициент деформации бесконечно
малого вектора, исходящего из
при отображении
.
![]() означает, что все бесконечно малые
вектора, исходящие из
,
при отображении
деформируются с одним и тем же масштабом,
то есть сохраняют постоянное растяжение.
означает, что все бесконечно малые
вектора, исходящие из
,
при отображении
деформируются с одним и тем же масштабом,
то есть сохраняют постоянное растяжение.
![]() растяжение
растяжение
![]() не деформируется
не деформируется
![]() сжатие
сжатие
![]()

![]()


![]() - произвольная гладкая кривая
- произвольная гладкая кривая
![]()
![]() ,
,
![]()
![]() -
угол наклона касательной к
в точке
.
-
угол наклона касательной к
в точке
.
![]() - угол наклона касательной к
- угол наклона касательной к
![]() в точке
в точке
![]() .
.
![]() ,
,
![]() .
.
![]()
![]()
![]()
![]() ,
,
![]() .
.
![]() - угол, на который нужно повернуть вектор,
касательный к кривой
в точке
,
с тем, чтобы совместить его с направлением
вектора, касательного к кривой
,
при отображении
на
- угол, на который нужно повернуть вектор,
касательный к кривой
в точке
,
с тем, чтобы совместить его с направлением
вектора, касательного к кривой
,
при отображении
на
![]() ,
осущ.
аналитической функции.
,
осущ.
аналитической функции.
Отображение осущ. аналитической функции сохраняет углы между прямыми.
Отображение
- аналитическая функция в точке
,
![]() ,
удовлетворяющее двум свойствам:
постоянство растяжения; сохранение
углов – комфорное отображение.
,
удовлетворяющее двум свойствам:
постоянство растяжения; сохранение
углов – комфорное отображение.
