
- •20. Основы метода конечных элементов, этапы решения, матричная форма записи уравнений теории упругости. Функции формы конечного элемента.
- •21. Матрица жесткости конечного элемента. Разрешающие уравнения метода конечных элементов.
- •22. Ползучесть, основы моделей ползучести. Теория старения.
- •23. Теория течения и теория упрочнения модели. Установившаяся ползучесть. Длительная прочность.
- •24. Экспериментальное исследование прочности гтд. Определения. Оценка статической прочности. Оценка динамической прочности.
- •25.Эци. Испытания лопаток, замковых соединений, ободов дисков. Способы измерения деформации. Стратегии управления ресурсом.
- •26. Теория колебаний. Связи. Обобщенные координаты. Виртуальные перемещения. Обобщенные силы. Условия равновесия.
- •27. Уравнения Лагранжа. Свободные колебания системы с одной степенью свободы.
- •29. Нормальные координаты и главные колебания.
- •30. Уравнение частот, собственные формы колебаний и их свойства.
20. Основы метода конечных элементов, этапы решения, матричная форма записи уравнений теории упругости. Функции формы конечного элемента.
Сущность метода. Любую напрерывную функцию можно апроксимировать моделью, состоящую из отдельных элементов или участков. На каждом из элементов исследуемая величина апроксимируется кусочно-непрерывной функцией, которая строится в конечном числе точек элемента. В общем случае непрерывная величина считается неизвестной, необходимо определить ее значение во внутренних точках области.
Этапы решения.
1) область разбивается на конечное число подобластей, называемых элементами. Они имеют общие узловые точки и в совокупности апроксимируют форму области.
2) В области фиксируется конечное число узлов, часть из них общие. Определяются координаты этих точек.
3) Значение непрерывной величины в узлах принимается известным, при расчете они уточняются в соответствии с наложенными граничными условиями в зависимости от задачи.
4) Используя значения функции в узлах, определяют значение функции в любой точке.
Матричная форма записи уравнений теории упругости.
Перемещение:
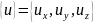
Закон Гука:
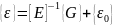
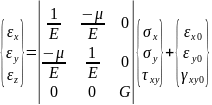
Начальная деформация:
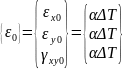
Уравнения Коши:
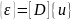
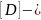 матрица деференцирования
матрица деференцирования
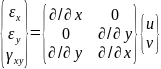
Функции формы конечного элемента.
Рассмотрим стержневой
элемент длиной
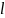 ,
поперечным сечением
,
поперечным сечением
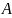 и модулем Юнга
и модулем Юнга
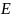 .
Введем две функции
.
Введем две функции
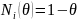 ,
,
 ,
где
,
где
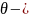 относительная координата точки элемента
в локальной СК:
относительная координата точки элемента
в локальной СК:
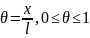 .
.
Смещение любой точки
в пределах элемента
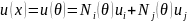 .
.
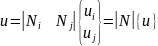
Линейная функция
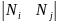 называется функцией формы стержневого
элемента. Она апроксимирует перемещения
в пределах элемента.
называется функцией формы стержневого
элемента. Она апроксимирует перемещения
в пределах элемента.
21. Матрица жесткости конечного элемента. Разрешающие уравнения метода конечных элементов.
Матрица жесткости
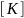 связывает между собой узловые усилия
и перемещения, включает физические
константы материала.
связывает между собой узловые усилия
и перемещения, включает физические
константы материала.
Для стержневого элемента:
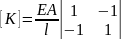
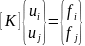
Для балочного элемента:
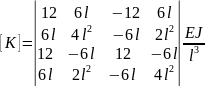
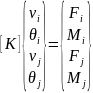
Разрешающие уравнения МКЭ.
Линейный плоский
треугольный элемент. Позволяет
апроксимировать геометрические области
любой формы. Каждый узел имеет две
степени свободы. Смещение
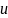 и
и
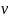 в любой точке внутри элемента является
линейными функциями координат этой
точки.
в любой точке внутри элемента является
линейными функциями координат этой
точки.
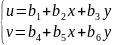
Деформации в пределах элемента являются постоянными:
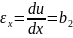
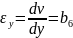
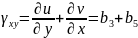
Перемещения узловых точек элемента определяется уравнениями:
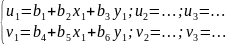
Перемещения точки в пределах элемента через функцию формы:
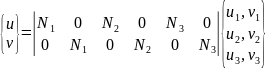
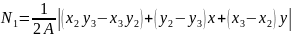
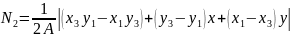
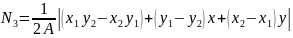
Деформация в точках элемента:
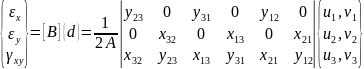
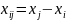
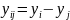
С вводом локальной СК функция упрощается:
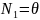
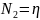
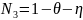
Перемещение точки:
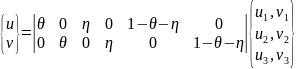
Связь ЛСК и глобальной СК:
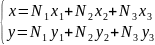
После разбиения тела, приложения граничных условий и нагрузок, формируется матрица жесткости системы, вектора угловых смещений и усилий.
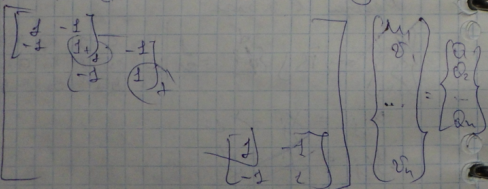
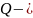 вектор узловых усилий: температурных,
поверхностных и массовых.
вектор узловых усилий: температурных,
поверхностных и массовых.
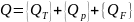
Решение данной системы позволяет определить перемещение → деформации → напряжения.
22. Ползучесть, основы моделей ползучести. Теория старения.
Ползучесть – возрастание деформации с течением времени при постоянном нагружении (в металле при высокой температуре). Приводит к перераспределению напряжений и может явится причиной недопустимых деформаций элементов конструкции.
Основы моделей ползучести.
Общая деформация является суммой деформаций ползучести, упругости, пластичности и температурных деформаций.
Скорость деформации ползучести пропорциональна составляющим девиаторам напряжения.
Теория старения.
Согласно ТС, существует
зависимость
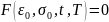 ,
где
,
где
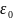 и
и
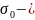 суммарные деформации и напряжения при
заданном времени и температуре нагружения
при простом растяжении.
суммарные деформации и напряжения при
заданном времени и температуре нагружения
при простом растяжении.
При сложном напряженном
состоянии (много осей) дополнительно
используется зависимость
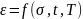 .
.
В условиях стационарного нагружения эти функции определяются экспериментально. Температурные деформации не учитываются. На основании полученных данных определяются изохорные кривые ползучести.
В теории старения допускается, что данные зависимости справедливы при настационарном нагружении. Ползучесть приводит к уменьшению упруго-пластического сопротивления материала, условные кривые деформации понижаются (уменьшается модуль Юнга, предел прочности и другие механические свойства), материал состаривается.
При известных изохорных кривых ползучести задача ТП сводится к решению задачи теории пластичности с переменными параметрами, где вместо кривой деформации принимаются изохорные кривые для соответствующего момента времени. На практике ТС применима при монотонном нагружении, что является ее основным недостатком.
