
- •Вопрос 1 Вектор. Линейные операции над векторами. Базисы на плоскости и в пространстве. Декартова система координат. Проекции и координаты вектора.
- •Вопрос 4 Матрицы и их основные свойства. Действия над ними
- •Вопрос 8. Векторное произведение векторов. Основные свойства. Векторным произведением вектора на вектор называется вектор, обозначаемый символом и определяемый следующими тремя условиями:
- •Вопрос 10. Различные способы задания прямой на плоскости.
- •Вопрос 11. Взаимное расположение двух прямых на плоскости.
- •Вопрос 15. Расстояние от точки до плоскости.
- •Вопрос 16. Различные способы задания прямой в пространстве.
- •Вопрос 17. Взаимное расположение прямой и плоскости. Расстояние от точки до прямой в пространстве.
- •Вопрос 18. Эллипс. Каноническое уравнение.
- •Вопрос 20. Парабола. Каноническое уравнение.
- •Вопрос 21. Классификация кривых второго порядка.
- •Вопрос 22. Поверхности второго порядка.
- •Вопрос 23. Линейное пространство. Базис и размерность линейного пространства.
- •Вопрос 24. Линейный оператор. Матрица линейного оператора. Ядро и образ линейного оператора.
- •Вопрос 25. Матрица линейного оператора в новом базисе.
- •Вопрос 26. Собственные векторы и собственные значения линейных операторов.
- •Вопрос 27. Теорема Кронекера-Капелли.
- •Вопрос 28. Решение системы линейных уравнений методом Крамера.
- •Вопрос 29. Решение системы линейных уравнений методом Гаусса.
- •Вопрос 30. Решение системы линейных уравнений матричным методом.
- •Вопрос 31. Множества и операции над ними.
- •Вопрос 32. Свойства действительных чисел.
- •Вопрос 33. Модуль действительного числа. Неравенство треугольника.
- •Вопрос 34. Грани числовых множеств.
- •Существование грани множества
- •Принцип вложенных отрезков
- •Вопрос 35. Числовые последовательности (предел, переход к пределу в неравенствах)
Вопрос 23. Линейное пространство. Базис и размерность линейного пространства.
Определение
линейного пространства
Пусть V -
непустое множество (его элементы будем
называть векторами и обозначать ![]() ...),
в котором установлены правила:
...),
в котором установлены правила:
1)
любым двум элементам ![]() соответствует
третий элемент
соответствует
третий элемент ![]() называемый
суммой элементов
называемый
суммой элементов ![]() (внутренняя
операция);
(внутренняя
операция);
2)
каждому ![]() и
каждому
и
каждому ![]() отвечает
определенный элемент
отвечает
определенный элемент ![]() (внешняя
операция).
(внешняя
операция).
Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:
I. ![]()
II. ![]()
III. ![]() (нулевой
элемент, такой, что
(нулевой
элемент, такой, что ![]() ).
).
IV. ![]() (элемент,
противоположный элементу
(элемент,
противоположный элементу ![]() ),
такой, что
),
такой, что ![]()
V. ![]()
VI. ![]()
VII. ![]()
VIII. ![]() Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается C).
Базис
пространства
Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается C).
Базис
пространства ![]() .
Координаты вектора
.
Координаты вектора
Базис
- любая упорядоченная система ![]() из n линейно
независимых векторов пространства
.
из n линейно
независимых векторов пространства
.
Обозначение: ![]()
Для
каждого вектора ![]() существуют
числа
существуют
числа ![]() такие,
что
такие,
что
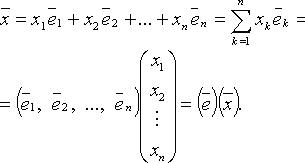
Числа ![]() называются
координатами вектора
в
базисе (
)
(определяются однозначно), X
= (x) -
координатный столбец вектора
в
этом базисе. Употребляется запись:
называются
координатами вектора
в
базисе (
)
(определяются однозначно), X
= (x) -
координатный столбец вектора
в
этом базисе. Употребляется запись: ![]()
Справедливы формулы:
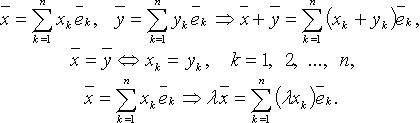
Вопрос 24. Линейный оператор. Матрица линейного оператора. Ядро и образ линейного оператора.
Линейные оператор
Пусть
заданы линейные пространства ![]() и
и ![]() .
Правило, по которому каждому
элементу
.
Правило, по которому каждому
элементу ![]() ставится
в соответствие единственный элемент
ставится
в соответствие единственный элемент ![]() ,
называется оператором,
действующим в линейных пространствах
,
называется оператором,
действующим в линейных пространствах ![]() .
Результат действия оператора
.
Результат действия оператора ![]() на
элемент
на
элемент ![]() обозначают
обозначают ![]() или
или ![]() .
Если элементы
и
.
Если элементы
и ![]() связаны
соотношением
,
то
называют образом элемента
;
элемент
связаны
соотношением
,
то
называют образом элемента
;
элемент ![]() прообразомэлемента
.
прообразомэлемента
.
Множество
элементов линейного пространства
,
для которых определено действие
оператора
,
называют областью
определения оператора
и обозначают ![]() .
.
Множество
элементов линейного пространства
,
которые являются образами элементов
из области определения оператора
,
называют образом оператора
и обозначают ![]() .
Если
,
то
.
Если
,
то ![]() .
.
Оператор , действующий в линейных пространствах называется линейным оператором,
если ![]() и
и ![]() для
любых
для
любых ![]() и
для любого числа
и
для любого числа ![]()
Если пространства и совпадают, то говорят, что оператор действует в пространстве .
Линейный оператор и его матрица. Переход к другому базису
Рассмотрим
линейный оператор
,
действующий в конечномерном линейном
пространстве
,![]() и
пусть
и
пусть ![]() базис
в
.
Обозначим через
базис
в
.
Обозначим через ![]() образы
базисных векторов
образы
базисных векторов ![]() .
.
Матрица

столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.
Доказано,
что каждому линейному оператору,
действующему в n-мерном линейном
пространстве, отвечает единственная
квадратная матрица порядка n; и
обратно ![]() каждая квадратная
матрица порядка n задает единственный
линейный оператор, действующий в этом
пространстве. При этом соотношения
каждая квадратная
матрица порядка n задает единственный
линейный оператор, действующий в этом
пространстве. При этом соотношения
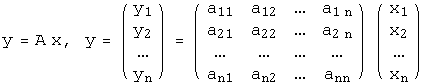
с одной стороны, связывают координаты образа с координатами прообраза , с другой стороны, описывают действие оператора, заданного матрицей .
При
изменении базиса линейного пространства
матрица оператора, очевидно, изменяется.
Пусть в пространстве
произошел
переход от базиса ![]() к
базису
к
базису ![]() .
Связь между матрицей
.
Связь между матрицей ![]() оператора
в
базисе
оператора
в
базисе ![]() и
матрицей
и
матрицей ![]() этого
оператора в базисе
этого
оператора в базисе ![]() задается
формулой .
задается
формулой .
![]()
Здесь ![]() матрица
перехода от базиса
к
базису
и
обратная к ней.
матрица
перехода от базиса
к
базису
и
обратная к ней.
Образ и ядро линейного оператора
Рассмотрим
линейный оператор
,
действующий в конечномерном линейном
пространстве
.
Доказано, что образ
линейного
оператора
линейное
пространство. Размерность образа
линейного оператора называется рангом
оператора,
обозначается ![]() .
.
Ядром
линейного оператора называется
множество элементов из
,
образом которых является нулевой
элемент. Ядро оператора обозначают ![]() :
: ![]() .
Ядро линейного
оператора
линейное
пространство; размерность ядра линейного
оператора называется дефектом оператора,
обозначается
.
Ядро линейного
оператора
линейное
пространство; размерность ядра линейного
оператора называется дефектом оператора,
обозначается ![]() :
: ![]() .
.
Для линейного оператора, действующего в n-мерном линейном пространстве , справедливы следующие утверждения:
сумма
ранга и дефекта оператора равно
размерности пространства, в котором
действует оператор: ![]() ;
;
ранг оператора равен рангу его матрицы;
ядро оператора совпадает с множеством решений линейной однородной системы с матрицей , размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.
Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
