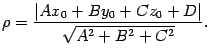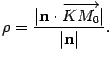Вопрос 15. Расстояние от точки до плоскости.

 Пусть плоскость   задана уравнением   и дана точка   . Тогда расстояние   от точки   до плоскости   определяется по формуле

(11.7)

       Доказательство.     Расстояние от точки   до плоскости   -- это, по определению, длина перпендикуляра   , опущенного из точки   на плоскость   (рис. 11.9).

Рис.11.9.Расстояние от точки до плоскости

Вектор   и нормальный вектор n плоскости   параллельны, то есть угол   между ними равен 0 или   , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

(11.8)

Координаты точки   , которые нам неизвестны, обозначим   . Тогда   . Так как   , то   . Раскрыв скобки и перегруппировав слагаемые, получим

(11.9)

Точка   лежит на плоскости   , поэтому ее координаты удовлетворяют уравнению плоскости:   . Отсюда находим, что   . Подставив полученный результат в формулу (11.9), получим   . Так как   , то из формулы (11.8) следует формула (11.7). 

Вопрос 16. Различные способы задания прямой в пространстве.

Уравнение прямой в пространстве, заданной точкой M0 и направляющим вектором p→ Oe1→e2→e3→−  аффинная система координат M0(x0,y0,z0)−  точка; p→(p1,p2,p3)−  направляющий вектор;

d[M0,p→]−?  Берем произвольную точку M(x,y,z), для того чтобы она принадлежала нашей прямой d необходимо и достаточно, чтобы −−−−−−→M0M∣∣p→ , поэтому: если p1/=0 ; p2/=0 ; p3/=0 , то уравнение прямой в пространстве будет:

p1x−x0=p2y−y0=p3z−z0;

если p1/=0 ; p2/=0 ; p3=0, то уравнение прямой в пространстве будет:

p1x−x0=p2y−y0;z−z0=0;

если p1=0; p2=0; p3/=0 , то уравнение прямой в пространстве будет:

x−x0=0;y−y0=0; 

Остальные варианты аналогично.

Уравнение прямой в пространстве, заданной двумя точками Oe1→e2→e3→−  аффинная система координат M1(x1,y1,z1);M2(x2,y2,z2)−  точки; p→(p1,p2,p3)−  направляющий вектор;

d[M0,p→]−?  Составляем вектор −−−−−−−→M1M2(x2−x1,y2−y1,z2−z1)  и тогда нужно найти уравнения прямой в пространстве, заданной точкой M1 и направляющим вектором −−−−−−−→M1M2. Из предыдущего пункта уравнения прямой в пространстве будет:

x−x1x2−x1=y−y1y2−y1=z−z1z2−z1 Уравнение прямой в пространстве, заданной двумя плоскостями Даны 2 плоскости 

θ1:A1x+B1y+C1z+D1=0     (1)

θ2:A2x+B2y+C2z+D2=0     (2)

θ1⋂θ2=d 

Берем произвольную точку M(x,y,z), для того чтобы она принадлежала нашей прямой d необходимо и достаточно, чтобы она принадлежала плоскости θ1 и плоскости θ2. Чтобы найти каноническое уравнение прямой надо знать координаты точки M0(x0,y0,z0), принадлежащей прямой d и вектора p→∣∣d . Координаты точки получим как решение системы (1) и (2). Для нахождения координат вектора p→(p1,p2,p3) воспользуемся следующей леммой. Лемма. Если прямая d в аффинной системе координат задана системой (1),(2), то вектор p→ с координатами:

p→(∣ ∣ ∣ ∣ ∣   B1   B2  C1   C2    ∣ ∣ ∣ ∣ ∣  ,∣ ∣ ∣ ∣ ∣   C1   C2  A1   A2    ∣ ∣ ∣ ∣ ∣  ,∣ ∣ ∣ ∣ ∣   A1   A2  B1   B2    ∣ ∣ ∣ ∣ ∣  )  Является направляющим вектором этой прямой. Параметрическое уравнение прямой в пространстве Oe1→e2→e3→−  аффинная система координат M0(x0,y0,z0)−  точка; p→(p1,p2,p3)−  направляющий вектор;

d[M0,p→]−? 

Берем произвольную точку M(x,y,z), для того чтобы она принадлежала нашей прямой d необходимо и достаточно, чтобы −−−−−−→M0M∣∣p→ , тогда параметрическое уравнение прямой:

x−x0=tp1;  y−y0=tp2;  z−z0=tp3;