Вопрос 33. Модуль действительного числа. Неравенство треугольника.

 Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.  Короче это записывают так:

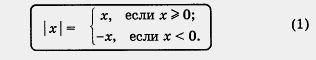Например,

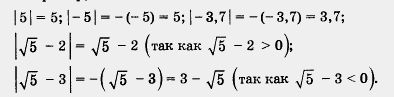На практике используют различные свойства модулей, например:  1. |а|  0.  2.|аb| =|a| |b|. 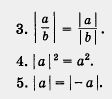 2. Геометрический смысл модуля действительного числа

Вернемся к множеству R действительных чисел и его геометрической модели — числовой прямой. Отметим на прямой две точки а и b (два действительных числа а и b), обозначим через   (a, b) расстояние между точками а и b (  — буква греческого алфавита «ро»). Это расстояние равно b - а, если  b > а (рис. 101), оно равно а - b, если а > b (рис. 102), наконец, оно равно нулю, если а = b. 

Все три случая охватываются одной формулой: 

Неравенство треугольника.

Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух сторон. Неравенство треугольника иногда включается как аксиома некоторой теории (например, оно включено в определение метрического пространства), в других оно появляется как теорема.

Нормированное пространство 

Пусть   — нормированное векторное пространство, где X — произвольное множество, а   — определённая на X норма. Тогда по определению последней справедливо:

Метрическое пространство

Пусть   — метрическое пространство, где X — произвольное множество, а   — определённая на Xметрика. Тогда по определению последней

Обратное неравенство треугольника 

Следствием неравенства треугольника в нормированном и метрическом пространствах являются следующие неравенства:

• 

• 

Вопрос 34. Грани числовых множеств.

Определения

Определение:

Если  , то A называется ограниченным сверху множеством.  называется верхней границей множества А. Если  , то A называется ограниченным снизу множеством.  называется нижней границей множества А. Если  , то A называется ограниченным множеством.

Определение:

Если   — ограничено сверху, то наимешьшая из его верхних границ называется верхней гранью.   ("супремум")

Определение:

Если   — ограничено снизу, то наибольшая из его нижних границ называется нижней гранью.   ("инфимум")

Существование грани множества

Теорема:

Если А ограничено сверху, то у него существует верхняя грань (аналогично для А, ограниченного снизу).

Доказательство:

Пусть M — множество верхних границ А. Так как А ограничено сверху, то  . По определению верхней границы:  . По аксиоме непрерывности: : .  — наименьшая из верхних границ А. Получили, что d — верхняя граница А, и d не больше всех верхних границ А  . Аналогично для нижней грани ограниченного снизу множества А.