3.2 Порядок виконання лабораторної роботи

1. Вивчити можливості MatLab по використанню прямих методів рішення СЛАУ.

2. Вивчити алгоритми ітераційних методів - ітерації Якобі та Зейделя.

3. Скласти відповідні програми-функції методів Якобі та Зейделя.

4. Виконати в MatLab індивідуальні завдання наведені в розділі 3.4.

5. Скласти звіт.

3.3 Основні теоретичні відомості

Розглянемо систему, що складається з m лінійних алгебраїчних рівнянь алгебри з n невідомими:

(3.1)

яка може бути записана в матричній формі

, (3.2)

де A – прямокутна матриця розмірності :

,

x – вектор n-ого порядку:

,

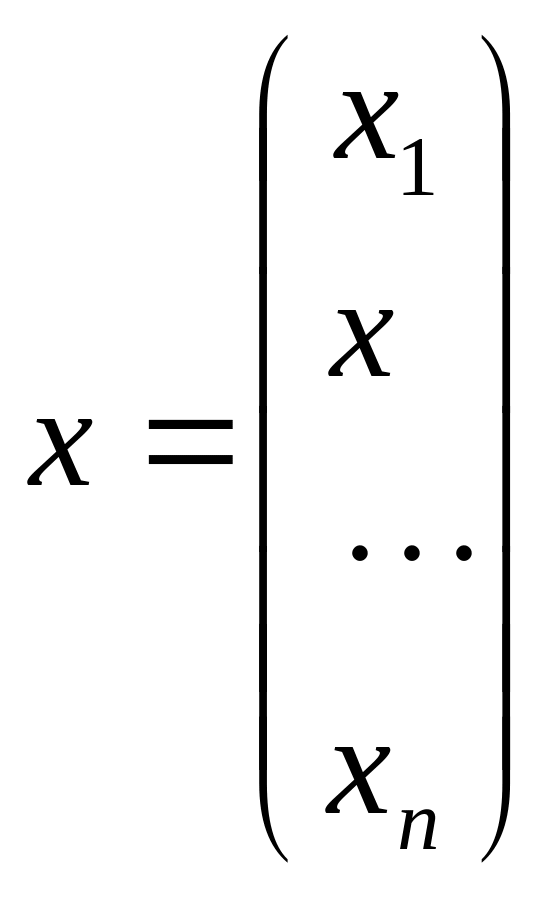b – вектор порядку m:

.

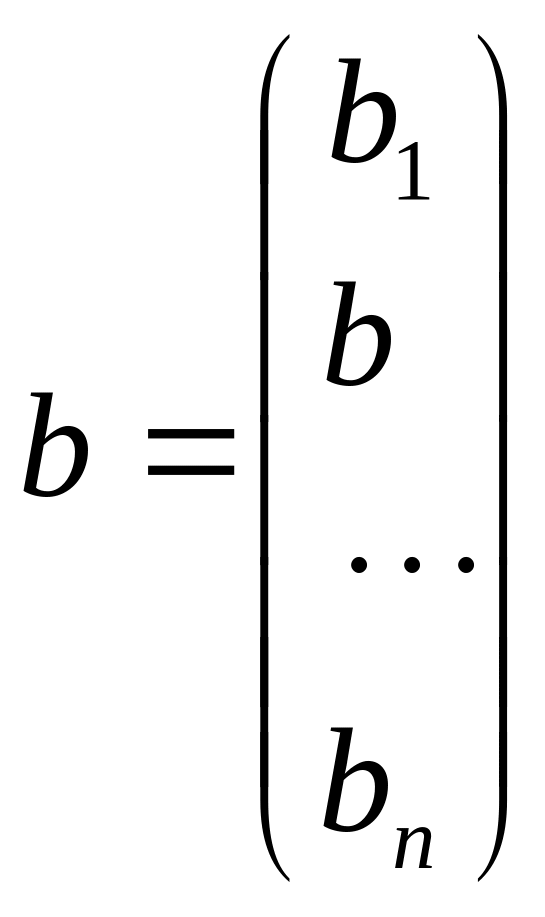Розв’язком системи називається така впорядкована сукупність чисел x: , що обертає всі рівняння системи (3.1) у тождества.

Припустимо, що матриця системи A задана і є неособливою, тобто визначник системи D ≠ 0. Відомо, що в цьому випадку вирішення системи існує, єдино і стійко за вхідними даними. На практиці, особливо при обчисленнях на комп'ютерах, коли відбувається округлення або відкидання молодших розрядів чисел, далеко не завжди удається отримати точну рівність визначника нулю. При D ≈ 0 розв’язок системи дуже чутливий до зміни коефіцієнтів системи. Таким чином малі похибки обчислень або початкових даних можуть привести до суттєвих похибок в рішенні. Такі системи рівнянь називаються погано обумовленими.

Методи розв’язання СЛАР діляться на дві групи:

- прямі методи;

- ітераційні методи.

3.3.1 Прямі методи і їх реалізація в пакеті MatLab

В прямих (або точних) методах кількість арифметичних дій, потрібних для отримання розв’язку x системи (3.1) є скінченним числом.

Істотним недоліком прямих методів є накопичення похибок в процесі, оскільки обчислення на будь-якому етапі використовують результати попередніх операцій. Це особливо небезпечно для великих систем, коли різко зростає загальне число операцій, а також для погано обумовлених систем, дуже чутливим до похибок.

Метод Гаусса

Розглянемо метод Гаусса розв’язання системи рівнянь. Прямий хід складається з m-1 кроків виключення.

1 Крок. Виключимо невідоме із рівнянь з номерами j = 2,3,..m. Припустимо, що . Називатимемо його провідним елементом 1-го кроку.

Знайдемо величини , звані множниками 1-го кроку. Віднімемо послідовно з другого, третього, ...m-го рівнянь системи перше рівняння, помножене відповідно на . В результаті 1-го кроку отримаємо еквівалентну систему рівнянь:

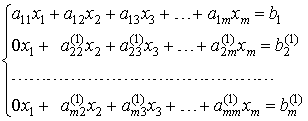
Аналогічно проводяться слідуючи кроки. Після (m-1)-го кроку виключення отримаємо систему рівнянь

,

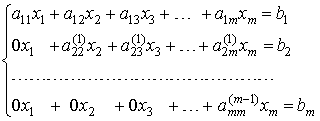матриця якої є верхньою трикутною. На цьому обчислення прямого ходу закінчуються.

Зворотний хід. Із останнього рівняння системи знаходимо . Підставляючи знайдене значення в передостаннє рівняння, отримаємо . Далі послідовно знаходимо невідомі: 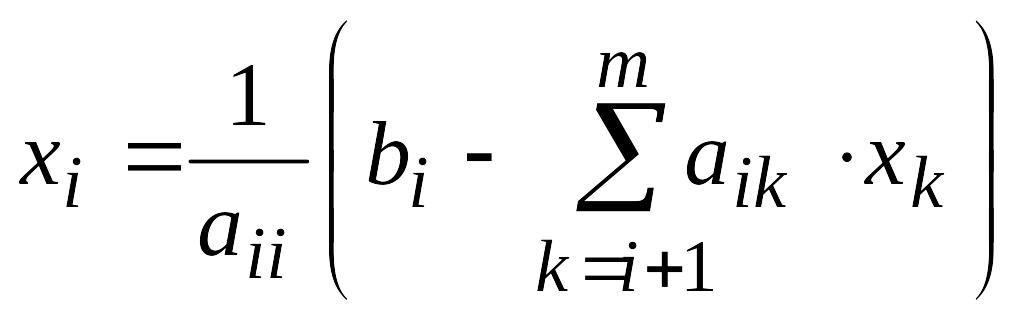, i=m-1, m-2, …, 3.

Метод Гаусса доцільно використовувати для вирішення систем з щільно заповненою матрицею і порядком системи n ≤ 100. Число арифметичних операцій приблизно рівне (2/3)n² .

Метод заснований на обчислені оберненої матриці А^-1

Система записується у вигляді АХ=В. Тоді, якщо помножити обидві частини цього векторного рівняння зліва на обернену матрицю А^-1, отримаємо

Х = А^-1В.

Проте, якщо не використовувати економічних схем для обчислення оберненої матриці, цей спосіб також непридатний для практичного вирішення лінійних систем при великих n(наприклад для n =10).

Метод Крамера

Менш трудомістким є метод Крамера, у якому значення невідомих можна отримати за допомогою формули

, i = 1, 2, … , n,

де матриця A_i формується з матриці A заміною її і-го стовпця на стовпець вільних членів

Можна спробувати використовувати це правило для вирішення систем рівнянь довільного порядку. Проте при великому числі рівнянь потрібно буде виконати величезне число арифметичних операцій. Кількість арифметичних операцій N =(n+1)(n*n!-1)+n. Вже коли n =50, такий об’єм обчислень практично недоступний сучасним комп’ютерам.

Реалізація прямих методів в системі MatLab

У системі MatLab для задачі вирішення системи лінійних рівнянь алгебри, одній з популярних в обчислювальній математиці, передбачені навіть "елементарні" операції.

Так для вирішення системи AX=B (A - матриця коефіцієнтів розмірності n*n, B- вектор правих частин розмірності n, Х векторів-стовпець невідомих) можна використовувати команду зворотного розподілу "\". Наприклад, для розв’язання системи

x1+2 x2+3 x3 = 3 5 x1+4 x2+3 x3 = 9 3 x1+4 x2+3 x3 = 6

задаємо матрицю коефіцієнтів і вектор правої частини

>> A=[1 2 3; 5 4 3; 3 4 3]

A =	1	2	3
	5	4	3
	3	4	3

>> B=[3 ; 9 ; 6 ]

B =	3
	9
	6

и виконати

>>X=A\B

Алгоритм розв’язання СЛАР за допомогою оператора \ у MatLab визначається структурою матриці коефіцієнтів системи. Під простотою рішення ховається досить серйозний аналіз структури матриці і використання кращого по точності і швидкодії алгоритму (метод Гаусса, розкладання Холецкого і ін.).

Для отримання оберненої матриці передбачена операція піднесення до ступеня -1 і функція inv(A):

>> A=[1 2 3; 5 4 3; 3 4 3] A = 1 2 3 5 4 3 3 4 3

>> C=inv(A) C = -0.0000 0.5000 -0.5000 -0.5000 -0.5000 3.0000 0.6667 0.1667 -0.5000

Нагадаємо, що обернення матриці може виявитися корисним при вирішенні системи AX=B у вигляді X=A^-1B:

>> B=[3 ; 9 ; 6 ] B = 3 9 6

>> X=inv(A)*B X = 3.5000 0 0.5000

Системи з погано обумовленими матрицями

Розглянемо простий приклад: потрібно знайти розв’язок системи:

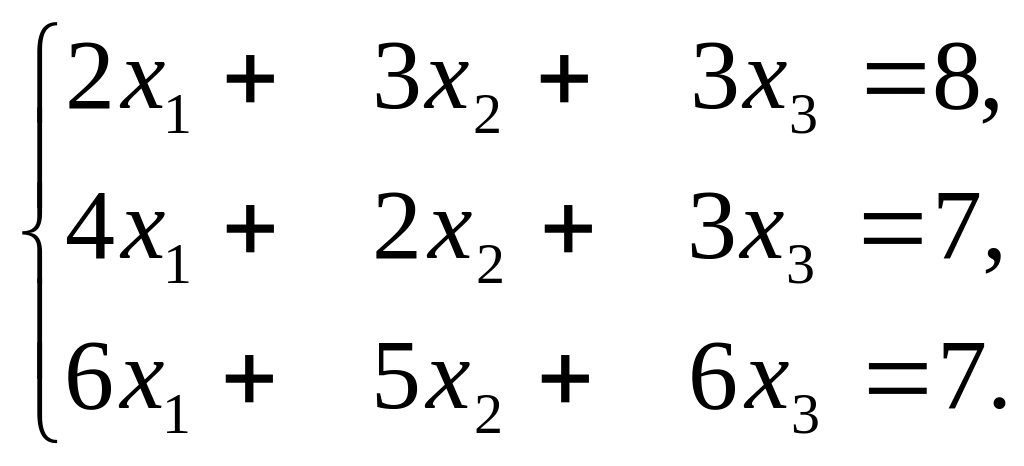
Розв’язання в MatLab:

>>A=[2 3 3

4 2 3

6 5 6];

>>B=[8;7;7];

>>x=A\b

Warning: Matrix is close to singular or badly scaled.

Results may be inaccurate.

x=3.e+016*

0.9007

3.8014

-4.4019

У командне вікно виводиться попередження про те, що матриця вироджена або погано обумовлена, і розв’язок x. Розв’язок невірний, в чому нескладно переконатися перевіркою, помноживши А на х.

Спроможність знаходження розв’язку системи лінійних рівнянь алгебри визначається числом обумовленості матриці. Перед розв’язуванням системи має сенс обчислити число обумовленості матриці системи за допомогою вбудованої функції cond, задавши аргументом матрицю А, де cond(A)= - відносне число обумовленості системи.

Якщо число обумовленості більше 10, то система є погано обумовленою, оскільки можливе сильне зростання похибки результату.