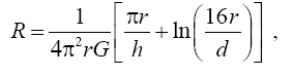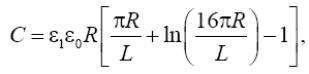5.5 Завдання на самостійну роботу
Решить нелинейную систему
С помощью Matlab нарисуйте графики обеих кривых в той же системе координат. Используйте график для проверки того, что существует 9 точек, в которых графики пересекаются. Используйте график, чтобы оценить точки пересечения.. Используйте эти оценки и метод Ньютона для приближения точек пересечения с 9 знаками.
5.6 Контрольні питання
Алгоритм метода простых итераций. В чем состоит сложность данного метода?
Алгоритм методу Ньютона.
Сформулюйте критерій закінчення ітераційного процесу рішення системи нелінійних рівнянь.
Можливості функції fsolve. Призначення аргументів(вхідних та вихідних) цієї функції.
Додаток 1 - - Індивідуальні завдання до робіт № 1, 2
№ |
1 |
2 |
1 |
3x4+4x3-12x2-5=0 |
ln(x)+(x+1)3=0 |
2 |
2x3-9x2-60x+1=0 |
x2x=1 |
3 |
x4-x-1=0 |
x+cos(x)=1 |
4 |
2x4 - x2-10=0 |
x+lg(1+x)=1.5 |
5 |
3x4+8x3+6x2-10=0 |
lg(2+x)+2x=3 |
6 |
x4 -18x2+5x-8=0 |
2x+5x-3=0 |
7 |
x4+4x3-12x2+1=0 |
5x+3x =0 |
8 |
x4 - x3-2x2+3x-3=0 |
3ex=5x+2 |
9 |
3x4+4x3-12x2+1=0 |
5x=6x+3 |
10 |
3x4-8x3-18x2+2=0 |
2ex+5x-6=0 |
11 |
2x4-8x3+8x2-1=0 |
2arctg(x)-x+3=0 |
12 |
2x4+8x3+8x2-1=0 |
(x-3) cos(x)=1 |
13 |
x4-4x3-8x2+1=0 |
xx= 20-9x |
14 |
2x4-9x3-60x2+1=0 |
x lg(x)=1 |
15 |
x5 +x2-5=0 |
tg3x=x-1 |
16 |
3x4+4x3-12x2-7=0 |
5x =1+e-x |
17 |
3x4+8x3+6x2-11=0 |
5x =3-ex |
18 |
x4 -18x3-10=0 |
arctg(x2+1/x)=x |
19 |
3x4-8x3-18x2+2=0 |
tg(0.55x+0.1)=x2 |
20 |
x4 -18x -10=0 |
5x-6x =7 |
21 |
x4 +18x -10=0 |
5x-6x =3 |
22 |
x4 +18x3-6x2+x-10=0 |
5x =1+e-2x |
23 |
x5 +12x3-6x2+x-10=0 |
7x-6x =2 |
24 |
3x5-8x3-18x2+2=0 |
5x =2+e-2x |
25 |
x3 -18x -10=0 |
x2x=3 |
Додаток 2. Варіанти завдань для підготовки до модульного контролю по темі «Розв’язання нелінійних рівнянь»
Нижче приведені варіанти завдань. Кожне з них включає варіанти, що відрізняються один від одного набором даних. Всі параметри у формулах, якщо не обумовлене інше, слід записувати в системі СІ.
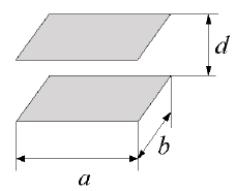
Завдання 1. Заземлітель у формі кільця радіусом r розташований в грунті на глибині h. Його сопротивление при h >> r розраховується по формулі:
|
|
де π = 3,14., G - електропровідність грунту, d - діаметр провідника з якого виготовлено кільце.
Задавшись параметрами h і d, вказаними в таблиці, а також прийнявши G = 0,03 1/Ом·м, знайдіть радіус r, що забезпечує необхідне сопротивление заземлення R .
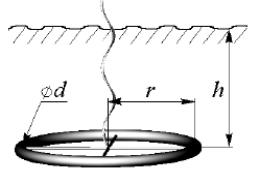
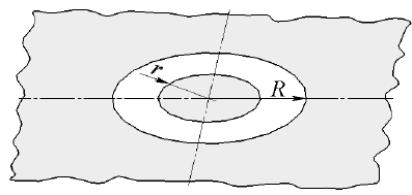
Завдання 2. Заземлітель, виготовлений у вигляді грат прямокутної форми з металевих труб|, розташований горизонтально в грунті на глибині h. Опір заземлителя розраховується по формулі
|
|
де π = 3,14…, L = 6×l − сумарна довжина труб, r − радіус труб, h − глибина, G − питома електропровідність грунту.
Задавшись параметрами r = 0,01 м, h (із таблиці), визначите розмір l, відповідний необхідному сопротивлению R.
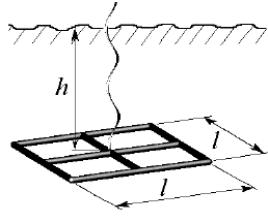
Завдання 3. Електрична ємкість системи двох паралельних пластин прямокутної форми (див. Малюнок) при a ≥ d і b ≥ d може бути визначена по формулі:
|
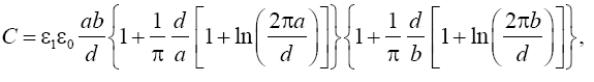
де ε1 − відносна діелектрична проникність середовища, ε0 = 8,85·10–12 Ф/м; a і b − розміри пластин; d − відстань між пластинами, π = 3,14…. Знайдіть зазор d, що забезпечує отримання необхідної ємкості C при вказаних в таблиці параметрах.
|
Завдання 4. Електрична ємкість двох коаксіальних плоских дисків (див. малюнок) при L/R<1 розраховується по формулі:
|
|
де ε1 − відносна діелектрична проникність середовища,
ε0 = 8,85·10–12 Ф/м, R − радіус дисків, L − відстань між дисками, π =3,14... .
Знайдіть радіус R, що задовольняє необхідному значенню ємності С, при заданих в таблиці параметрах ε1 и L .
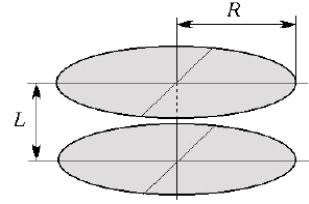
Завдання 5. У інтегральних схемах використовують планарные конденсатори, що мають вигляд металевого диска, розташованого в круглому вирізі металізації на поверхні діелектричної підкладки (див. малюнок). Ємкість такого конденсатора визначається по формулі: |
|
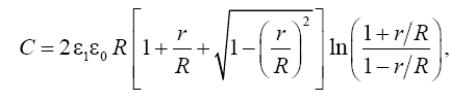
де ε1 − відносна діелектрична проникність діелектрика,
ε0 = 8,85·10−12 Ф/м, R − радіус вирізу, r – радіус диска.
Задавшись вказаними в таблиці параметрами ε1 і r, знайдіть радіус R, що забезпечує необхідну ємкість С.
Завдання 6 Для експериментально отриманої прямої гілки вольтамперної характеристики напівпровідникового діода при u < 0,6В В підібрана апроксимація у вигляді:
|
|
де ток i заданий в міліамперах, напруга u – у вольтах.
Використовуючи апроксимацію, знайдіть напругу на діоді, при якому через нього протікатиме заданий в таблиці ток i. При складанні рівняння використовуйте вказані в таблиці параметри a, b, c, d і e.
Параметр |
Варіант |
|||||
7-1 |
7-2 |
7-3 |
7-4 |
7-5 |
7-6 |
|
i,мА |
11 |
15 |
22 |
25 |
32 |
47 |
a,мА/В |
0,2 |
2,3 |
112 |
32 |
39 |
15 |
b,мА/В2 |
97 |
150 |
215 |
67 |
140 |
22 |
c,мА/В3 |
88 |
120 |
110 |
275 |
97 |
217 |
d,мА/В4 |
350 |
457 |
465 |
84 |
192 |
118 |
e,мА/В5 |
112 |
97 |
149 |
52 |
76 |
56 |
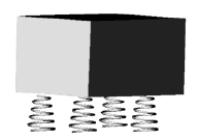
Завдання 7. Для захисту від вібрації блок літакової станції радіолокації встановлений на чотирьох амортизаторах. Система амортизації при цьому може мати до шести власних механічних резонансів, частоти яких визначаються рівнянням:
|
|
де A, B, C, D, E, F, G − коефіцієнти, що визначаються параметрами конструкції, ω – частота коливань.
Знайдіть резонансні частоти для заданих коефіцієнтів рівняння.
Параметр |
Варіант |
|||||
8-1 |
8-2 |
8-3 |
8-4 |
8-5 |
8-6 |
|
А |
0,01 |
0 |
0 |
0,1 |
1 |
0 |
B |
1 |
0,01 |
0,02 |
–20 |
0 |
0 |
C |
–78 |
1 |
0,1 |
102 |
–29900 |
1 |
D |
2,1e3 |
–1,25e3 |
–2,56e3 |
–8,98e3 |
0 |
–116 |
E |
-2,5e4 |
1,85e5 |
3,45e5 |
8,76e6 |
26400 |
4,3e3 |
F |
1,2e5 |
–8,75e6 |
–9,95e6 |
–7,5e5 |
9,12e8 |
–5,3e4 |
G |
–1,9e5 |
8,9e7 |
2,7e7 |
–3,3e8 |
–1,75e9 |
8,9e4 |