2. Розрахунки стосовно до режиму розчиненого газу

Режим розчиненого газу починається в пласті або з початку розробки його, якщо початковий пластовий тиск р_п дорівнює тиску насичення нафти газом р_н, або після виснаження пружної енергії, якщо поточний пластовий тиск р_п стає рівним тиску насичення р_н, тобто

Пластова енергія визначається кількістю розчиненого газу в одиниці об'єму нафти і рівномірно розподілена по покладу. Тому свердловини доцільно розташовувати по рівномірній (квадратній чи трикутній) сітці, якщо не передбачається заміна режиму розчиненого газу іншими режимами.

Розрахункова модель - це однорідний (за властивостями

колектора і нафти) пласт у вигляді кругового циліндра з

концентричною всередині свердловиною. Радіус основи циліндра

розраховується з формули об'єму циліндра за питомим

нафтонасиченим об'ємом порового простору (за балансовими

запасами нафти) покладу, який припадає на одну свердловину:

де - відповідно площа нафтоносності, ефективна товщина і коефіцієнт пористості порід покладу; - водонасиченість колектора; п - кількість свердловин.

При цьому відстані між свердловинами за квадратної сітки

становлять , а за трикутної сітки .

У методиці розрахунків прийнято, що відносні коефіцієнти проникності залежать тільки від насиченості nop нафтою, зв'язана вода відноситься до скелету породи, а ефектами гравітації, сегрегації, першою фазою режиму та інтерференцією свердловин можна знехтувати. Розрахунки виконують за методом послідовної зміни стаціонарних станів для одної свердловини, а отримані результати поширюють на весь поклад.

Для розрахунку показників розробки (дебітів, тисків, газового фактора, нафтовилучення і періоду розробки) потрібно попередньо визначити залежність між нафтонасиченістю s_K і тиском р_к на непро­никному контурі розрахункової моделі. Таку залежність отримано з рівнянь матеріального балансу для нафти і газу та виражено наближеною формулою (похибка, в основному, не перевищує 1%):

(2.31)

де - середній газовий фактор в інтервалі зміни тиску на контурі

моделі від за середнього тиску

насиченості на початку інтервалу:

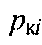
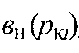
• маса газу в одиниці об'єму розчину за тиск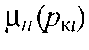у - об'ємний коефіцієнт і динамічний коефіцієнт в'язкості нафтИ за тиску ; 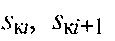- нафтонасиченість nop за тисків 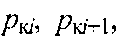причому 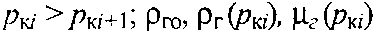- густина газу за стандартних умов (за тиску ро і температури То) та за тиску р_кі і пластової температури Т_ПЛ та іинамічний коефіцієнт в'язкості газу за тиску 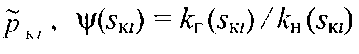- відношення відносних коефіцієнтів

проникностей газу і нафти .

Усі ці залежності властивостей нафти, газу, відносних коефіцієнтів проникностей беруть за лабораторними даними стосовно до розглядуваного покладу. Для зручності розрахунку у формулі (2.31) можна взяти таку рівність:

Яка випливає з рівняння Клапейрона - Менделєєва і в якому - коефіцієнт стисливості (надстисливості) нафтового газу як функція тиску за пластової температури.

Якщо відсутні залежності для розглядуваного покладу, то можна використати відповідні графіки або таблиці, які опубліковано в літературі. Залежність Ψ(S_кі) можна розрахувати за результатами попередньої дослідної розробки покладу. Для цього, використовуючи формулу (2.31), можна обчислити зміїгу нафтонасиченості від тиску за відомих значин газового фактора, з формули (2.32) визначити Ψ(s_ki) і побудувати графік її зміни. Це забезпечить більшу відповідність проектних і фактичних показників розробки.

Формула (2.31) дає змогу за значинами і на початку інтервалу знайти . Достатня точність розрахунку забезпечується за інтервалу зменшення тиску

Тоді поточний коефіцієнт нафтовилучення в разі режиму розчиненого газу за тиску буде:

- запаси нафти в пласті відповідно у початковий (за тиску і насиченості ) і в поточний момент часу; V- об'єм порового простору (без зв'язаної води).

Дебіт свердловини по нафті визначають за формулою:

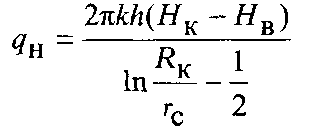
і дебіт по газу

де 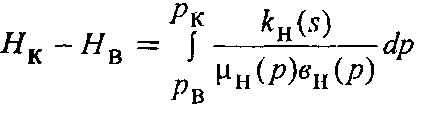- різниця узагальнених функцій.

Христиановича для відповідних тисків на контурі р_к і на вибої свердловини р_в.

Зв'язок між параметрами в часі встановлюють за рівнянням матеріального балансу для нафти, відповідно з яким різниця запасів нафти в пласті дорівнює накопиченому відбору нафти:

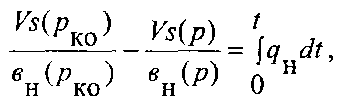
- нафтонасичений об'єм пор у початковий момент часу.

Після диференціювання рівняння та інтегрування дістанемо вираз для терміну розробки покладу:

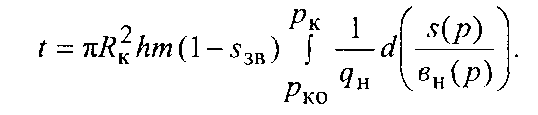
порядок розрахунків показників розробки залежить від заданих граничних умов на свердловині (або q_н= const, або р_в = const, або q_H і р_в змінні в часі).

За даними аналізу результати розрахунку значно залежать від неоднорідності пласта, темпів відбирання нафти. Так, коефіцієнт наф-товилучення, який розраховано для моделі однорідного пласта, є вищим (стосовно до родовища Жетибай на 17%) коефіцієнта нафто-вилучення, визначеного для моделі шарово-неоднорідного пласта, за один і той же термін розробки нафтового покладу (18 років). Для отримання такої ж значини коефіцієнта нафтовилучення (10%) неоднорідного пласта тривалість його розробки має бути в 2 рази більшою порівняно з розробкою однорідного пласта. Родовище розбурюється свердловинами протягом 3-5 років. Урахування інтер­ференції і темпів введення свердловин в експлуатацію призводить до зниження коефіцієнта нафтовилучення із елементів до 2,1-7,4% проти 12,5%, отриманих з розрахунків за розглянутою методикою.

Режим розчиненого газу малоефективний навіть у випадку малов'язких нафт. Якщо все-таки треба вирішувати питання щодо можливості існування його в покладі або щодо оцінки ефективності різних методів діяння на поклад (режим розчиненого газу береться за "базовий" варіант розробки), то для розрахунків показників розробки покладу на режимі розчиненого газу, доцільніше розв'язувати системи диференціальних рівнянь багатофазної фільтрації чисельними методами, наприклад, за методикою ВНДІ-2, яку розглянемо нижче.

Лекція 12.

Розрахунки технологічних показників розробки покладів у випадку витіснення нафти водою

1.Розрахунок показників розробки покладу з використанням методу еквівалентних фільтраційних опорів.

2.Основи теорії поршньового і непоршньового витіснень.

Водонапірний режим витіснення нафти водою - основний у практиці розробки нафтових родовищ. Тенденція в розвитку методик розрахунку технологічних показників, як зазначалось, полягає в максимальному наближенні математичних моделей до реальних умов родовищ (відмінність в'язкостей, багатофазність руху, неоднорідність пласта та ін.), у максимальному врахуванні особливостей будови кожного конкретного пласта.

Нижче, з методичних позицій щодо аналізу впливу різних природних і технологічних чинників на процес видобування нафти, послідовні» розглянуто аналітичний метод еквівалентних фільтраційних опоріи. основи теорії поршневого і непоршневого витіснень; принципові поли ження побудови сучасної розрахункової методики на прикладі методики ВНДІ-2, а також наближеної аналітичної методики ВЩЦ-1.

Розрахунок показників розробки покладу з використанням методу еквівалентних фільтраційних опорів

Метод еквівалентних фільтраційних опорів - основний аналітичний метод визначення кількісного зв'язку між дебітами свердловин і тисками на їх вибоях та на контурі живлення пласта (нагнітання води) в умовах жорсткого водонапірного режиму.

Суть методу полягає в заміні повного фільтраційного опору реаль­ному потокові рідин складної конфігурації кількома еквівалентними (рівнозначними) послідовними або паралельними фільтраційними опорами простіших (прямолінійно-паралельних, плоскорадіальних) потоків. Зрозуміло, що така заміна вносить певну похибку в результати розрахунку, яка проте допустима в разі недостатньої точності вхідної геолого-промислової інформації.

З підземної гідрогазомеханіки відомо принцип електрогідро-динамічної аналогії (ЕГДА), згідно з яким сила електричного струму / відповідає витраті рідини (дебіту, різниця напруг - різниці тисків (депресії тиску ), електричний опір провідника і - фільтраційному опору пласта .

Принцип ЕГДА легко виводиться з аналізу формул закону Дарсі або Дюпюї і закону Ома:

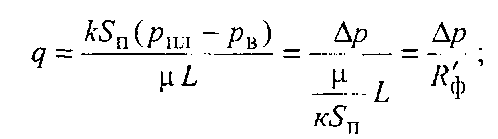
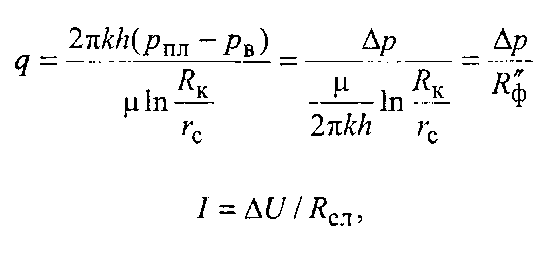
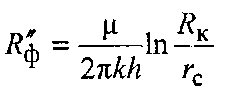де к - коефіцієнт проникності пласта; - площа поперечного перерізу і довжина смугоподібного пласта; (і - динамічний коефіцієнт в'язкості рідини; h, R_К - товщина і радіус контура кругового пласта; r_с - радіус свердловини - депресія тиску (різниця пластового р_пл і вибійного р_в тисків фільтраційний опір у смугоподюному пласті; фільтраційний опір у круговому пласті.

Дебіт одної свердловини в прямолінійному нескінченному ряді стосовно усталеного припливу однорідної нестисливої рідини можна записати.

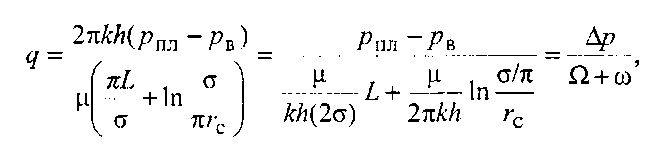
Перший доданок у знаменнику, як неважко помітити із зіставлення з формулою закону Дарсі, дорівнює фільтраційному опору в смугоподібному пласті на ділянці довжиною від контура пласта до галереї, розташованої на лінії ряду ("галереєзація" ряду). Площа поперечного перерізу пласта, яка припадає на дану свердловину з ряду, дорівнює добутку товщини пласта на ширину , що дорівнює відстані між свердловинами.

Другий доданок со дорівнює фільтраційному опору в круговому пласті з радіусом контура .

Отже, складний фільтраційний потік можна поділити на два простіших: прямолінійно-паралельний потік від контура пласта до галереї, розміщеної на лінії ряду свердловин; плоскорадіальний потік у середині галереї в круговому пласті з довжиною контура , тобто . Величину прийнято називати зовнішнім фільтраційним опором (на зовнішньому шляху від контура до галереї), а - внутрішнім фільтраційним опором (всередині галереї), який враховує збільшення опору припливу рідини у свердловину порівняно з галереєю, довжина якої . Сума опорів означає їх послідовне з'єднання. Аналогічно для кругового пласта дебіт одної свердловини в концентричному круговому ряді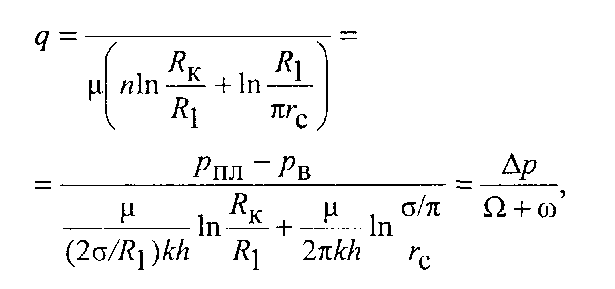

кількість свердловин у ряді; - радіус лінії розміщення кругового ряду свердловин.

Перший доданок . у знаменнику є фільтраційним опором частини кругового пласта (сектор з кутом радіан) від контура до кругової галереї довжиною і радіусом а другий доданок - внутрішнім фільтраційним опором припливу до свердловини всередині галереї в круговому пласті з довжиною контура тобто У цьому разі складний потік до одної свердловини в круговому ряді можна поділити на плоскорадіальний потік від контура до кругової галереї і плоскорадіальний потік до свердловини всередині галереї.

Дебіти відповідно прямолінійного і колового рядів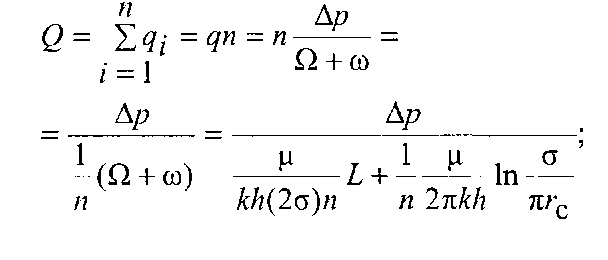

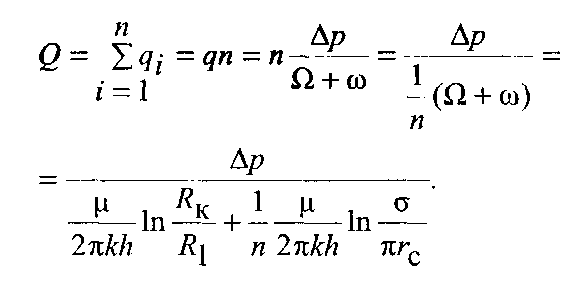
Звідси випливає, що приплив до усіх свердловин можна розглядати як паралельне з'єднання провідників з однаковими опорами Таким чином, фільтраційний потік до свердловини можна подати еквівалентною схемою електричних опорів і для розрахунку використовувати закони Ома і Кірхгофа (перший або другий закон), розуміючи відповідно до принципу ЕГДА, під силою струму, різницею напруг і електричними опорами їх аналоги - витрату рідини, перепад тисків, фільтраційні опори.

Стосовно до багаторядної системи свердловин пласт також подається простою геометричною формою - прямокутною або круговою. Реаль­ий потік між свердловинами сусідніх рядів замінюється фільтрацією між "проникними" галереями з внутрішніми фільтраційними опорами свердловин всередині галереї, які доповнюють зовнішні фільтраційні опори між галереями. Тоді, подаючи фільтраційну схему пласта еквіва­лентною їй електричною схемою опорів і застосовуючи стосовно останньої закони Ома і Кірхгофа, складають рівняння інтерференції рядів свердловин для розрахунку дебітів або вибійних тисків.

Складемо ці рівняння для кільцевого (кругового) однорідного за проникністю і товщиною пласта з коловими концентричними рядами свердловин (рис. 2.1).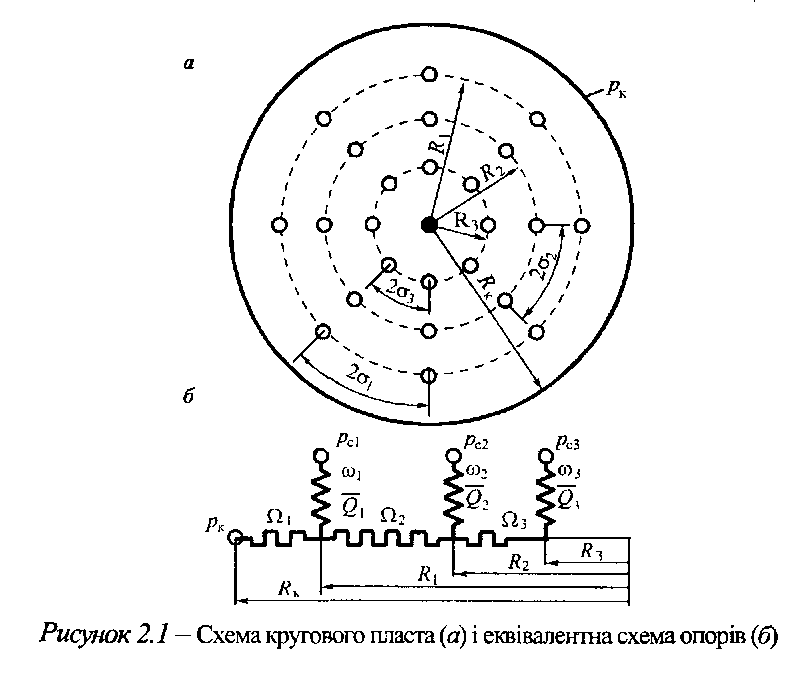

Для цього використаємо другий закон Кірхгофа, згідно з яким на основі ЕГДА перепад тиску між двома точками схеми дорівнює сумі добутків дебіту рідини в межах ділянки на фільтраційний опір цієї ділянки. Отримаємо систему рівнянь інтерференції

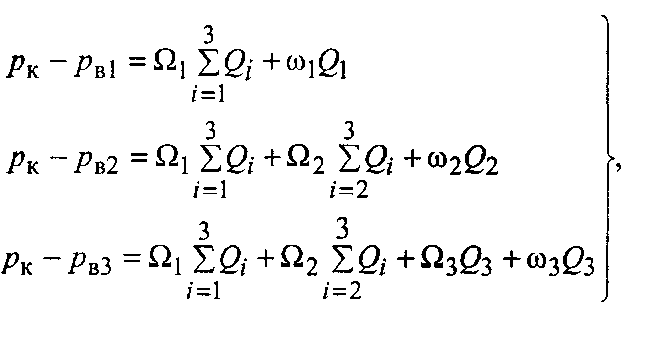
(взаємодії) рядів свердловин:де р_к - тиск на контурі живлення пласта; р_в1 - вибійні тиски свердловин і-го ряду; - дебіт усіх свердловин і-го ряду; внутрішній фільтраційний опір, однаковий

для кругових (кільцевих) і смугоподібних пластів;

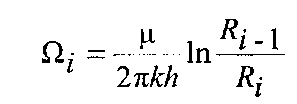- внутрішній фільтраційний опір і-го ряду; радіус і кількість свердловин, - половина відстані між свердловинами і -го ряду - радіус і-го ряду свердловин.

Поклад можна схематизувати сектором, тоді у вирази замість потрібно підставити величину кута сектора в радіанах.

Кількість рівнянь у системі має дорівнювати кількості рядів свердловини.

Аналогічні рівняння інтерференції складають для смугоподібного покладу, лише зовнішній фільтраційний опір і відстань між

свердловинами відповідно становлять де

• - ширина покладу; 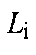- відстань між сусідніми рядами або між контуром живлення і першим рядом.

Узагальнене рівняння інтерференції рядів свердловин у багаторядних системах для смугоподібного і кругового (кільцевого) покладів на основі системи рівнянь (2.45) можна записати так:

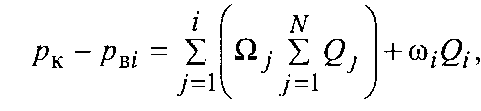
де - відповідно кількість рядів, що передує j-му ряду, і загальна кількість одночасно працюючих рядів.

Під час проектування задача розв'язується стосовно до однієї з таких граничних умов: а) задано вибійні тиски; б) задано дебіти свердловин; в) в одних рядах задано вибійні тиски, а в інших - дебіти свердловин. Тоді визначають відповідні величини: дебіти, вибійні тиски або дебіти і вибійні тиски.

Звичайно задають вибійні тиски, виходячи з технологічних і технічних умов (мінімальний вибійний тиск фонтанування сверд­ловин, допустимий ступінь зниження вибійного тиску нижче тиску насичення нафти газом та ін.). Тоді із системи рівнянь типу (2.45) визначають дебіти рядів свердловин ( сумарний відбір із покладу

(дебіт покладу) . Зазначимо, що знайдені таким чином дебіти є сталі в часі. Тоді загальний термін розробки можна знайти діленням величини видобувних запасів нафти на сумарний відбір. Накопичений видобуток нафти на будь-який момент часу легко розрахувати множенням дебіту на тривалість часу розробки. Поточний коефіцієнт нафтовилучення визначається відношенням поточного накопиченого видобутку до балансових запасів.

Аналіз результатів розрахунку за рівняннями інтерференції показує, що за однакових вибійних тисків в усіх свердловинах одночасно можуть працювати не більше, ж три ряди свердловин, тому що четвертий і наступний ряди практично повністю екрануються роботою перших трьох рядів. При цьому дебіт другого ряду становить приблизно ЗО...40%, а третього - 15...20% дебіту першого ряду або дебіти рядів дорівнюють відповідно 60...70, 30...20 і 5... 10% сумарного відбору. Якщо у свердловинах зовнішніх рядів підтримувати вищі вибійні тиски, ніж у внутршшіх рядах, то дебіти зовнішніх і внутрішніх рядів значною мірою вирівнюються, проте загальний відбір із покладу зменшується.

Ряди свердловин можуть також працювати за умови двосто­роннього напору (живлення), який можливий у смугоподібному і круговому покладах у разі внутрішньоконтурного нагнітання води в центральний коловий ряд нагнітальних свердловин і природного за-контурного напору пластової води. У випадку двостороннього напору один будь-який із внутрішніх рядів (звичайно центральний) візьмемо як потокорозділювальний ряд, в який рідина притікає з двох сторін. Систему рівнянь інтерференції можна скласти за трьома способами:

а) аналогічно системі рівнянь (2.45) для лівої і правої частин схеми;

б) на відміну від першого способу в системі рівнянь записуємо витрати рідини між рядами, а дебіти рядів обчислюємо як різницю відповідних ряду витрат;

в) рівняння складаємо згідно з першим законом Кірхгофа для вузлів схеми (кількість рідини, що притікає до вузла схеми дорівнює кількості рідини, що витікає із цього вузла, які можна подати як відношення різниці тисків на ділянці до відповідного фільтраційного опору); знаходимо тиски у вузлах схеми, потім, поділивши перепад тиску між лінією ряду і вибоями свердловин на відповідний внутрішній фільтраційний опір ряду, визначаємо дебіт ряду.

Якщо розрахункова схема симетрична, то обчислення зводяться до випадку одностороннього живлення. Оскільки дійсного положення потокорозділювального ряду не знаємо, то одна із складових його дебіту може мати від'ємну значину, що означає відсутність припливу з цієї сторони. У відповідному напрямі треба перемістити потокорозді­лювальний ряд і знову виконати розрахунки.

І врешті зазначимо, що розглядання подано стосовно до фільтрації однорідної (однакової густини і в'язкості) нестисливої рідини в одно­рідному за проникністю й анізотропному плоскому пласті до доско­налих свердловин за однакових умов (дебітів і вибійних тисків) роботи свердловин у межах кожного ряду. Метод еквівалентних фільтра­ційних опорів можна застосувати у випадку граничних положень ВНК, тобто коли в пласті рухається лише нафта або лише вода (після повного обводнення).

На використанні методу еквівалентних фільтраційних опорів базуються методики ВНДІ-1, ТатНДШнафта та ін.