Лекція №6 Приплив нафти і газу до свердловини.

1. Порушення лінійного закону при фільтрації нафти і газу.

2. Особливості припливу газу та газоконденсатної суміші до свердловини.

1. Приплив газу до вибою свердловин за законом Дарсі

Закон Дарси (Анри Дарси, 1856) — закон фильтрации жидкостей и газов в пористой среде. Получен экспериментально. Выражает зависимость скорости фильтрации флюида от градиента напора:

где: u — скорость фильтрации, K — коэффициент фильтрации, І — градиент напора.

Процес розробки газового родовища характеризується нестаціонарністю (неуста­леністю) фільтрації газу в пласті. Нестаціонарна фільтрація реального газу в неоднорідному за колекторськими властивостями пористому середовищі описується нелінійним диференційним рівнянням в частинних похідних параболічного типу

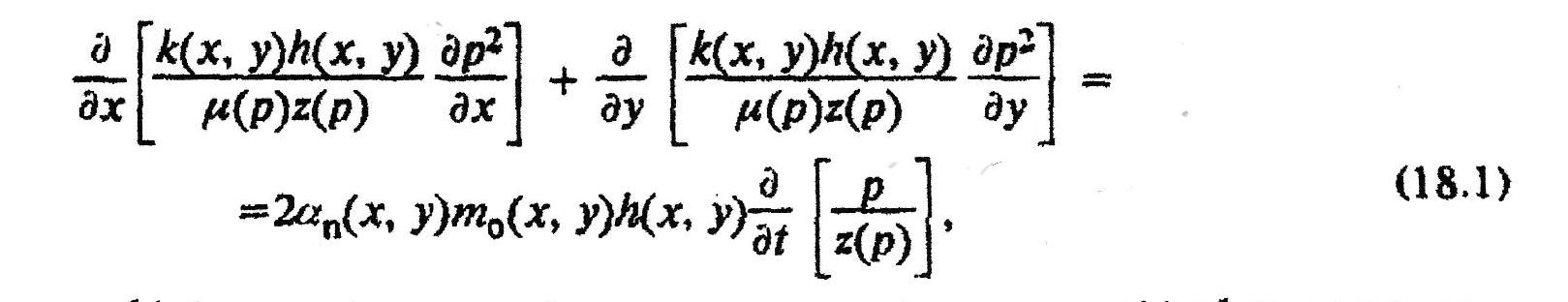
Де k,α_n,m₀,h - коефіцієнти проникності, газонасиченості, пористості і ефективна газонасичена товщина пласта в точці з координатами х і у; р — тиск в точці пласта з коорди­натами х і у в момент часу t\ μ(p), z(p) — відповідно коефіцієнти динамічної в’язкості і надстисливості газу при тиску р і пластовій температурі.

Для плоскорадіальної фільтрації реального газу в однорідному пласті рівняння (18.1) запишеться таким чином:

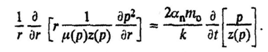
Диференційні рівняння фільтрації газу є нелінійними рівняннями параболічного типу. Нелінійність, зокрема, рівняння (18.5) пов'язана з наявністю в коефіцієнті перед похідною в часі шуканого тиску р. Нелінійні рівняння не мають точних аналітичних розв'язків. їх мож­на проінтегрувати чисельно за допомогою ЕОМ або розв'язати наближено аналітичними методами після зведення до лінійного вигляду.

Запропоновані різні способи лінеаризації диференційного рівняння нестаціонарної фільтрації газу. Всі вони мають певні погрішності розв'язків порівняно з точним розв'язком на ЕОМ нелінійного диференційного рівняння.

За невеликі проміжки часу тиск і густина в окремих точках пласта змінюються незнач­но, і приплив газу до свердловини можна розглядати як стаціонарний. Виходячи з цього, процес експлуатації окремих свердловин і розробки газового родовища можна зобразити як послідовну зміну стаціонарних станів.

Диференційні рівняння стаціонарної фільтрації газу в пласті одержуютьз (18.1)-(18.5), прирівнюючи до нуля похідні від тиску в часі (праві частини рівнянь).

Для розв'язання задач, пов'язаних з проектуванням розробки газового родовища, виз­наченням видобувних можливостей окремих свердловин, оцінкою ефективності обробки привибійної зони пласта тощо, використовують рівняння припливу газу до свердловини. При фільтрації газу за законом Дарсі його одержують в результаті розв'язання дифе-ренційного рівняння стаціонарної плоскорадіальної фільтрації газу при відповідних гранич­них умовах. На відміну від нестисливої рідини при фільтрації газу об'ємна витрата в на­прямі до свердловини безперервно зростає, тобто об'ємна швидкість фільтрації залежить не тільки від градієнта тиску, але і від величини тиску. Тому для газу закон Дарсі доцільно за­писувати через масову швидкість фільтрації (v_M = vp(p)):

де v, v_M — відповідно об'ємна і масова швидкості фільтрації газу, р(р) — густина газу при тиску р і пластовій температурі.

Масова витрата газу для будь-якого перетину пласта на відстані т від свердловини

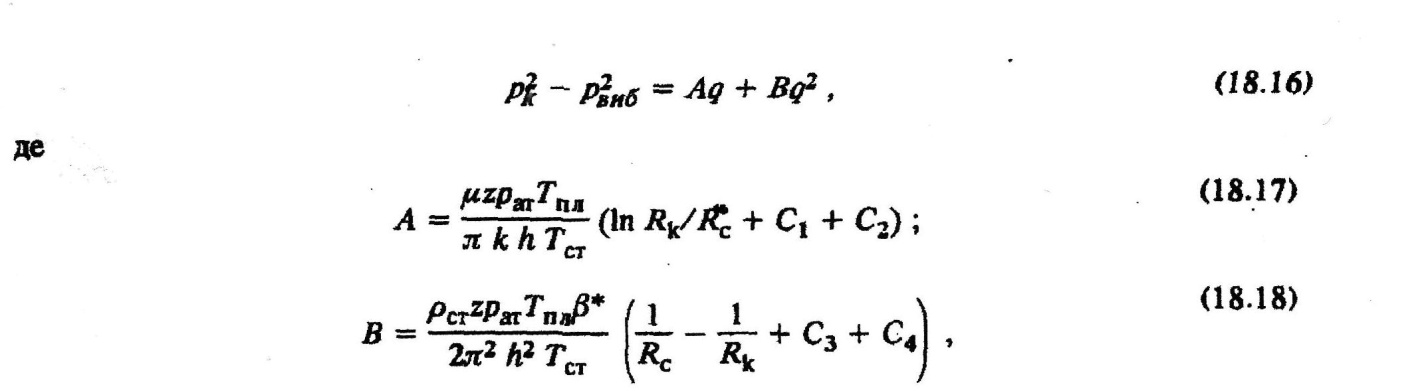
де А, В- коефіцієнти фільтраційних опорів привибійної зони пласта; р_ст- густина газу при

стандартних умовах; C_v С₂ І С₃, С₄ — коефіцієнти, які характеризують недосконалість свердловини за ступенем і характером розкриття пласта відповідно лінійної і квадратичної частин у двочленній формулі припливу газу.

Коефіцієнти недосконалості за ступенем розкриття пласта C_t і С₃ визначають за фор­мулами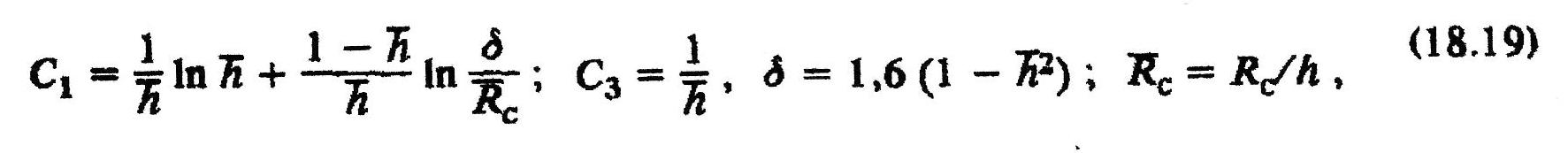

Де h= h _роз/ h — відносне розкриття пласта свердловиною (відношення розкритої і загаль­ної товщин пласта).

Коефіцієнти недосконалості за характером розкриття пласта С₂ і С₄ залежать від кількості отворів, типу перфорації, глибини і діаметра каналів і характеристик пористого середовища. У випадку сферичного припливу газу до напівсфери, яка утворилася за цемен­тним каменем, коефіцієнти С₂ і С₄ можна оцінити за формулами:

де п — кількість перфораційних отворів на їм товщини пласта; R₀ — радіус перфо­раційної напівсфери (каверни), який при кульовій перфорації приймають рівним 0,02 --0,03 м.

Для визначення структурного коефіцієнта β* запропоновано ряд кореляційних залеж­ностей:

залежність Г.О.Зотова