Отсюда находим S = 3S₁= .

12. Вычисление длины дуги

Линия (L) в пространстве называется гладкой, если в каждой точке (L) можно провести касательную к этой линии. Если линия без самопересечений задана параметрическими уравнениями

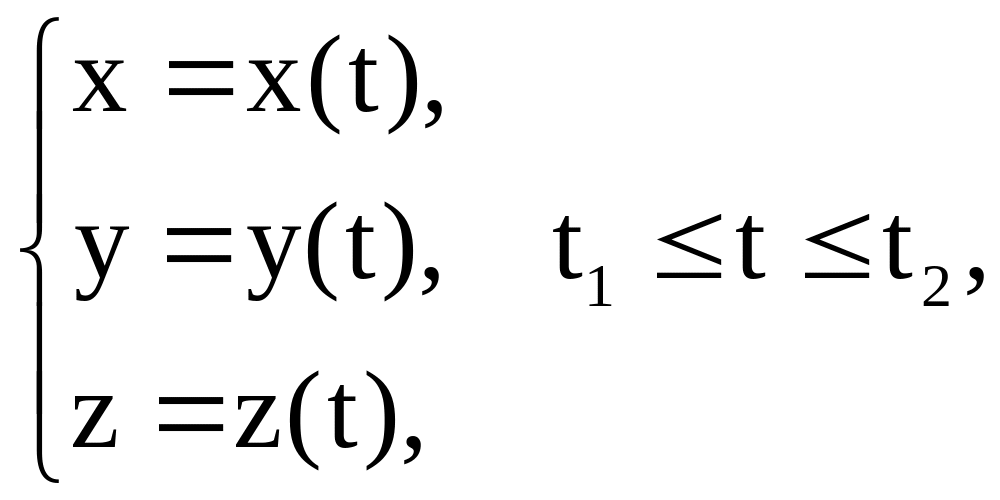
то дифференцируемость x(t), y(t), z(t) гарантирует гладкость линии; аналогичное утверждение справедливо для плоской линии. Если линия без самопересечений на плоскости с заданной полярной системой координат определена полярным уравнением , то и в этом случае дифференцируемость влечёт гладкость этой линии.

Если гладкая линия (L) на плоскости (в пространстве) задана параметрическими уравнениями , (и вдобавок к этому для линии в пространстве), , то длина линии (L) находится по формуле

( ).

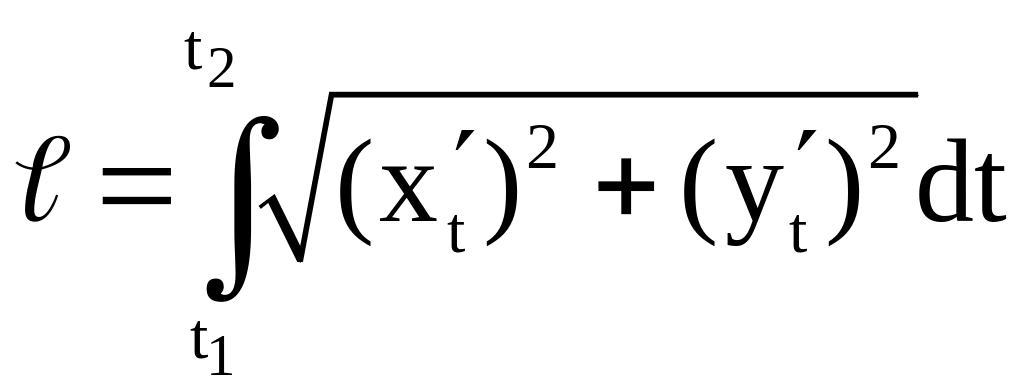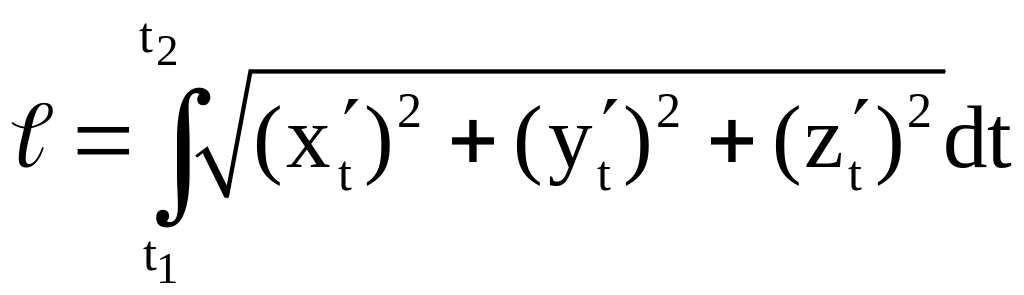Если гладкая линия (L) задана явным уравнением , , то .

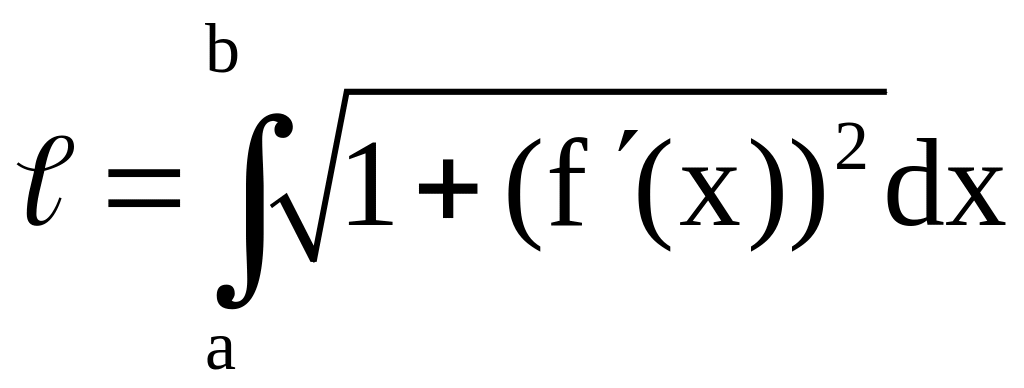Для гладкой линии (L), заданной полярными уравнениями, , .

Пример 26. Найти длину линии, заданной уравнением , , .

Решение. Имеем

.

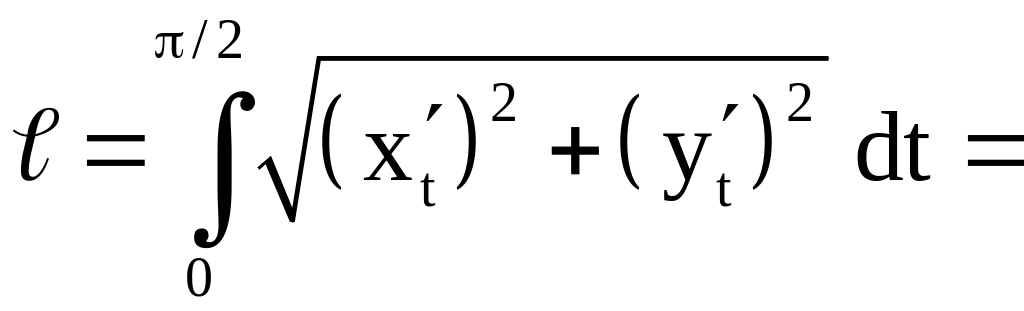
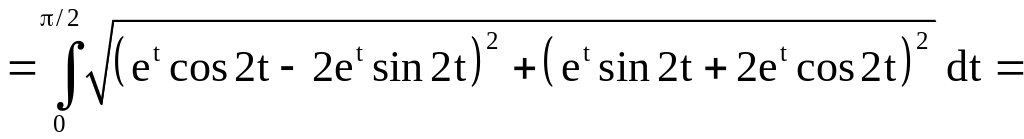
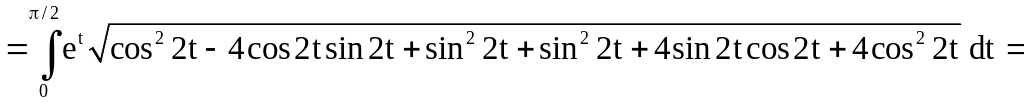
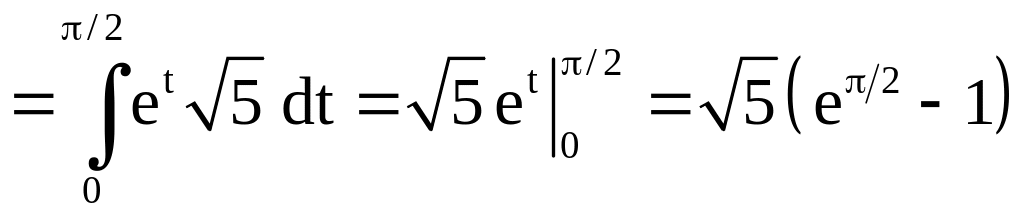Пример 27. Найти длину дуги логарифмической спирали , находящейся внутри окружности .

Решение. Дуге спирали, лежащей внутри окружности , соответствуют значения . Поэтому

.

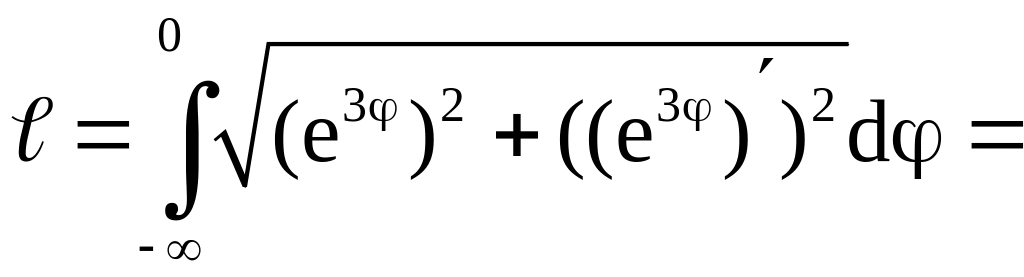
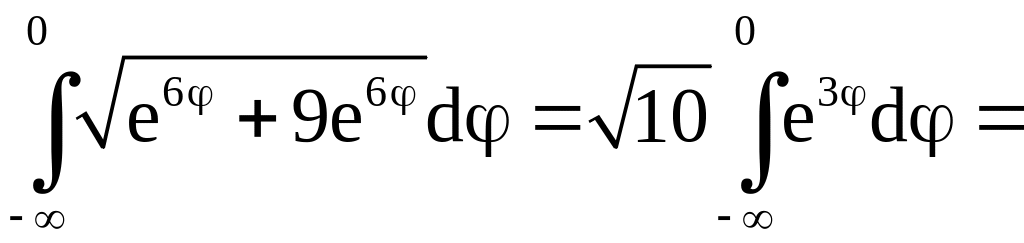
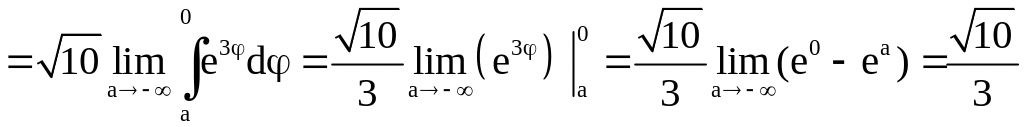13. Вычисление объёмов тел

Если в пространстве заданы ось 0х, тело (Т), проекцией которого на 0х является отрезок [a; b] , и для любого x  [a; b] известна площадь S(x) поперечного сечения S(x), то объём V тела (Т) находится по формуле

.

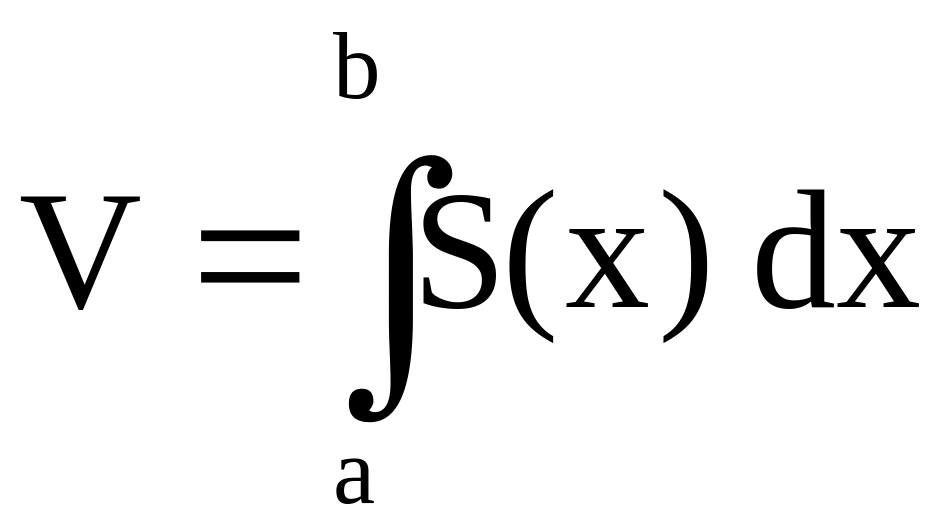В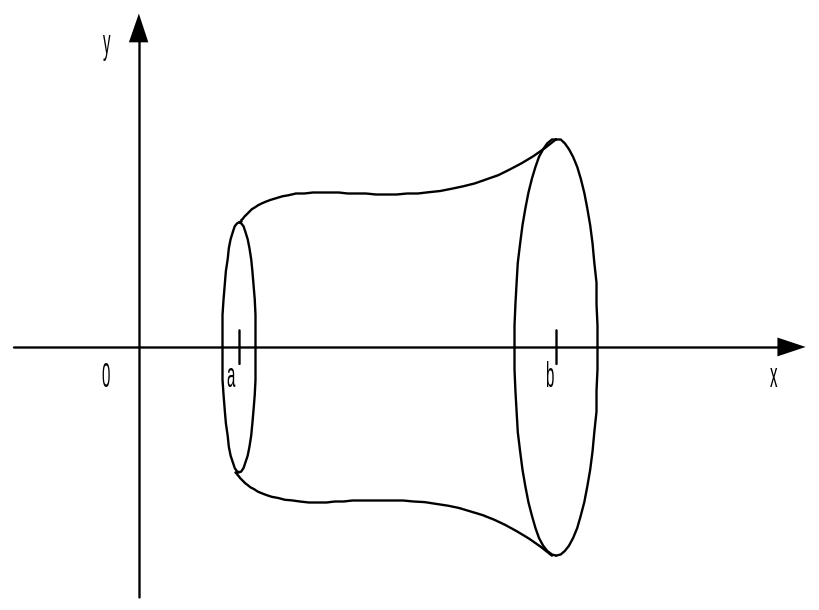 частности, если тело (Т) получено путём вращения графика функции , вокруг оси 0х, то объём тела вращения равен .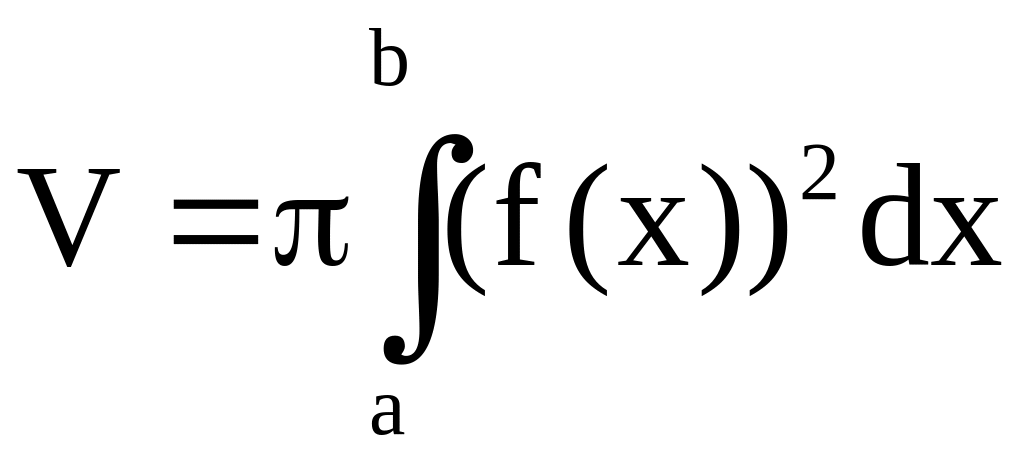

При вращении графика функции f(x) вокруг оси 0у формула объёма принимает вид

.

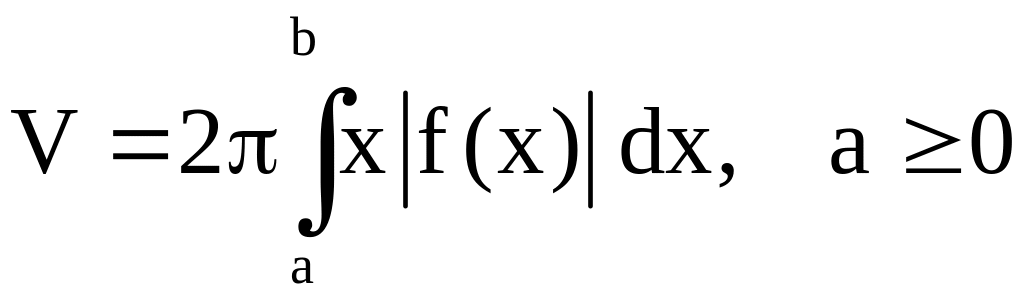Пример 28. Найти объём V тела (Т), ограниченного эллипсоидом

.

Решение. Проекцией тела (Т) на ось 0х является отрезок [–a; a]. Найдём формулу площади S(x) поперечного сечения,

x  [a; b]. Перепишем уравнение эллипсоида в виде

.

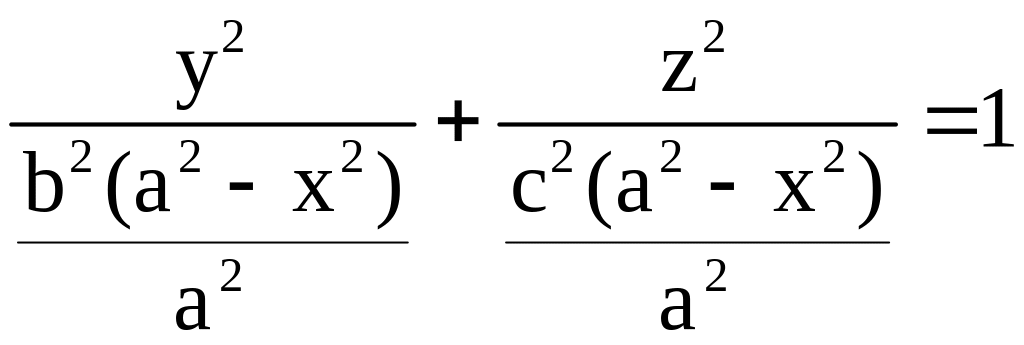Это есть уравнение поперечного сечения эллипсоида плоскостью, проходящей через точку x и перпендикулярной оси 0х. А мы уже знаем (задача 22), что площадь фигуры, заключённой внутри этого эллипса, равна 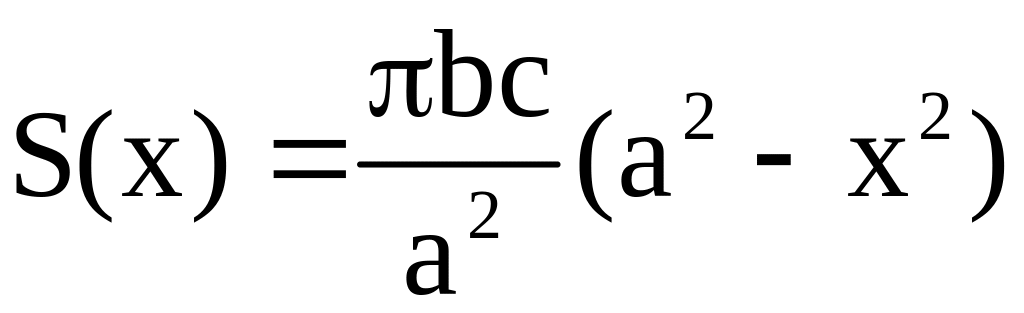. Следовательно,

.

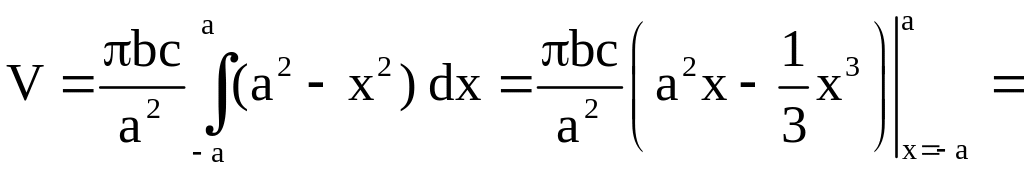
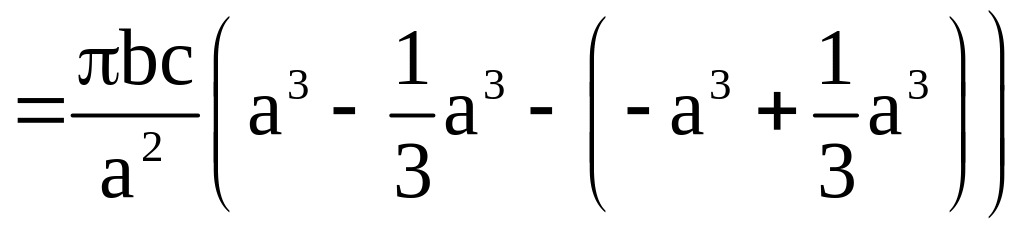
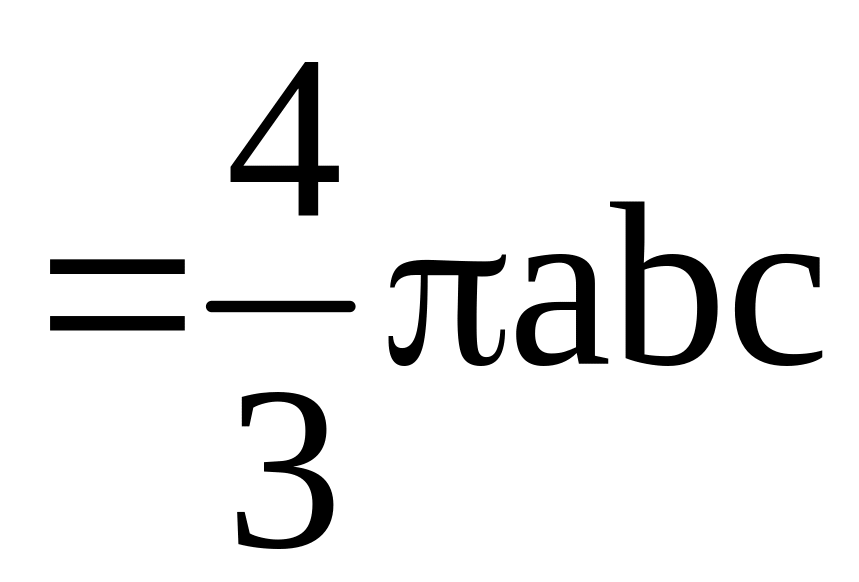14. Приближённое вычисление определённых интегралов

Формула Ньютона–Лейбница является хорошим средством для вычисления определённого интеграла. Однако возможности применения этой формулы сильно ограничены тем, что далеко не для всякой элементарной функции первообразная к ней является элементарной функцией. Другими словами, если f(x) является элементарной функцией, то могут оказаться неэлементарными функциями (более того, если f(x) образовать наобум как суперпозицию элементарных функций, то, скорее всего, будут неэлементарными функциями). В таком случае говорят, что является неберущимся интегралом. Приведём несколько таких примеров: 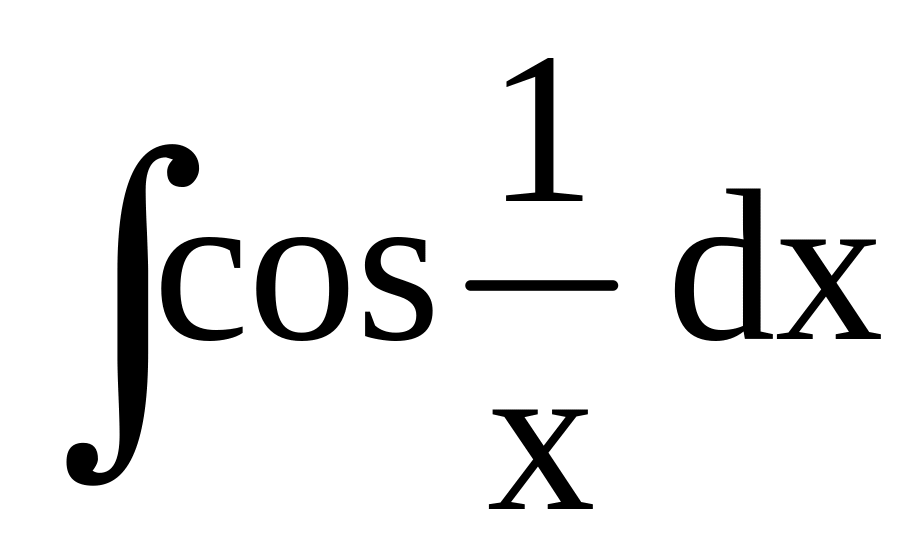, , 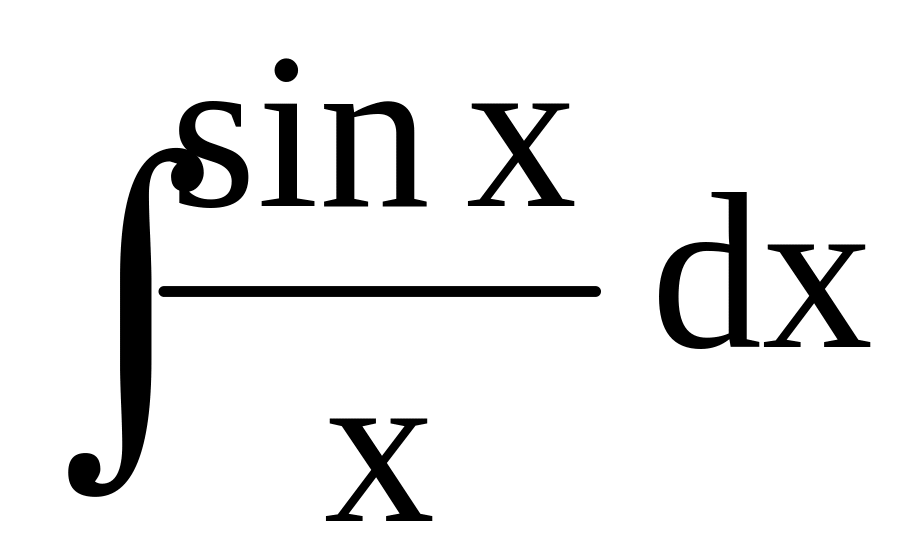, . Дело обстоит так, что в большинстве случаев решение прикладных задач требует вычисления определённых интегралов от функций, первообразные которых выходят за рамки класса элементарных функций, что делает невозможным применение формулы Ньютона–Лейбница. В таких случаях довольствуются приближённым вычислением определённого интеграла, или, как говорят, применяют методы численного интегрирования. К простейшим методам численного интегрирования относятся методы прямоугольников, трапеций и парабол (Симпсона).

Разобьём отрезок [a;b] на n равных частей точками ; называется шагом разбиения. 

Обозначим   ,   , .

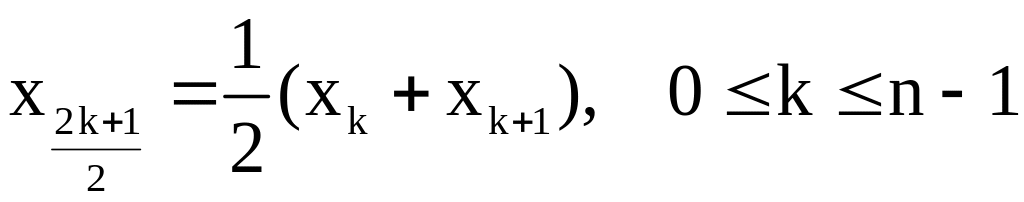По методу прямоугольников

;

;

.

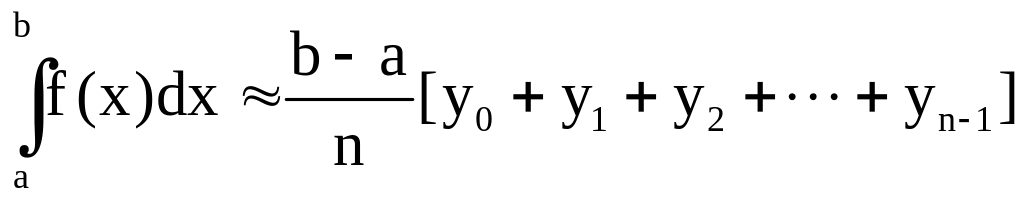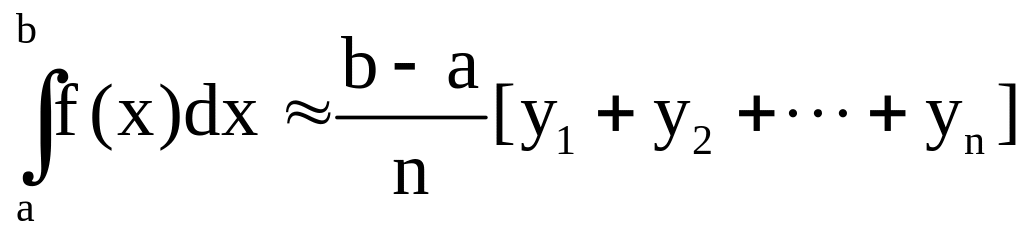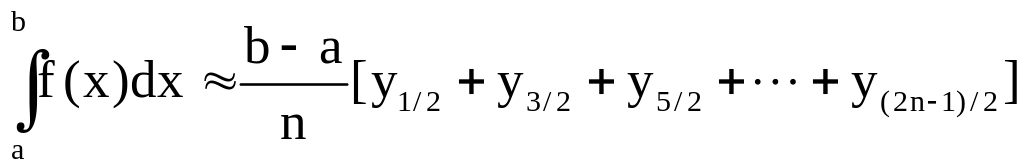Все эти три формулы называются формулами прямоугольников.

Метод трапеций состоит в применении формулы (при тех же обозначениях)

.

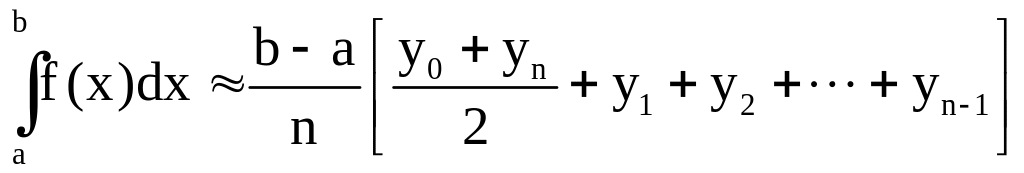В методе парабол (Симпсона) отрезок [a; b] разбивается на чётное число 2n отрезков равной длины точками a₁ = x₀ < x₁ < x₂ < …< x_2n = b. Согласно формуле Симпсона (при тех же обозначениях)

.

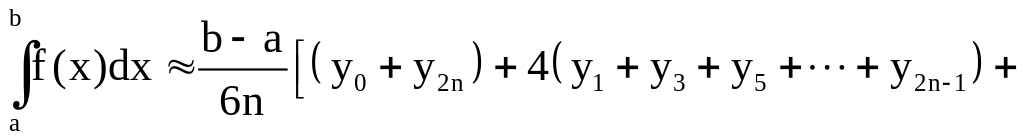
Точность вычисления растёт с ростом n. Погрешность R_n[f] приведённых выше формул оценивается величинами:

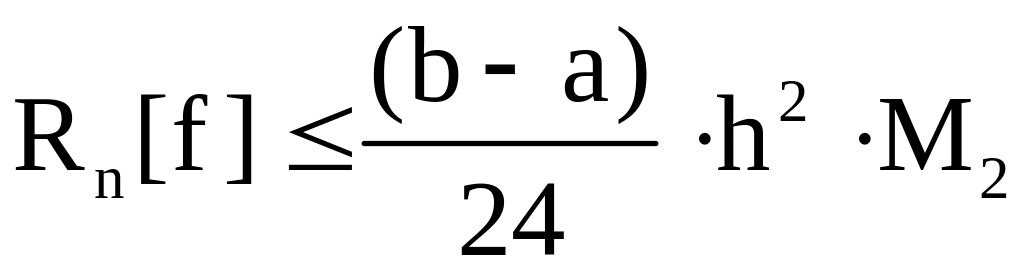для формулы прямоугольников ,

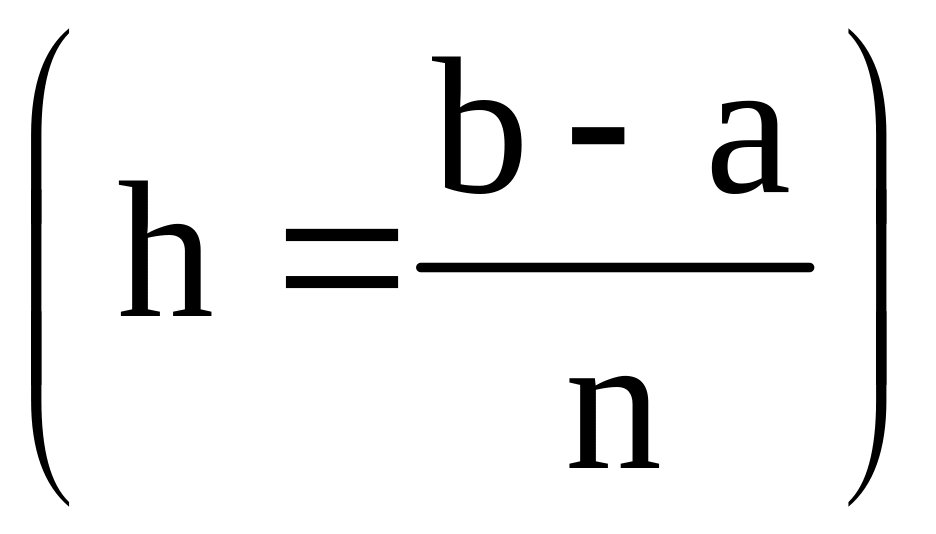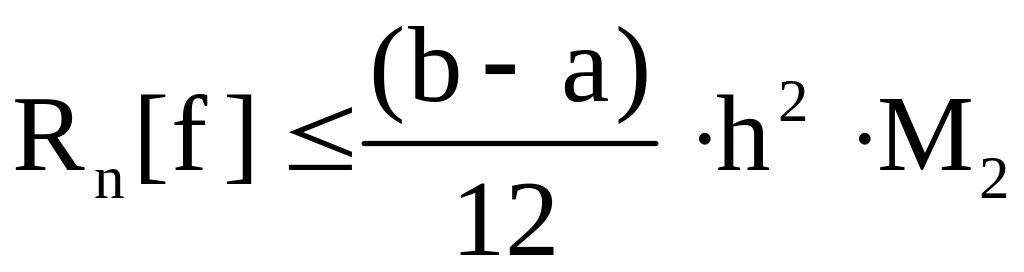для формулы трапеций ,

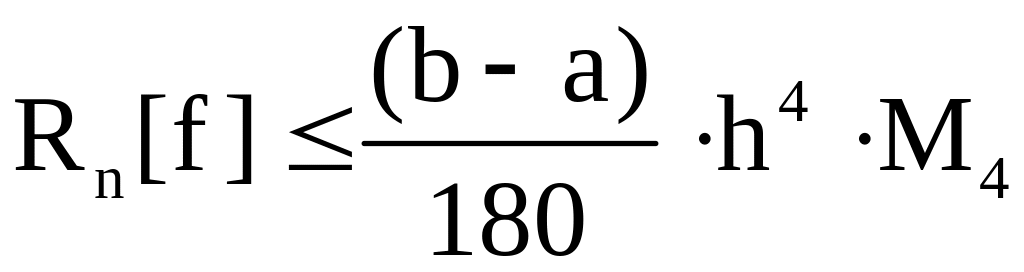для формулы Симпсона ,

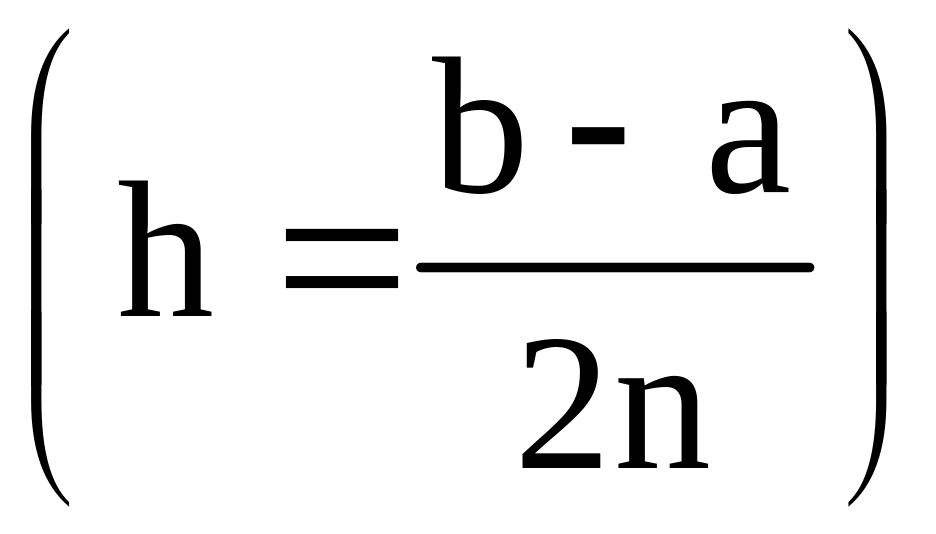где , .

Пример 29.   Вычислите приближённо 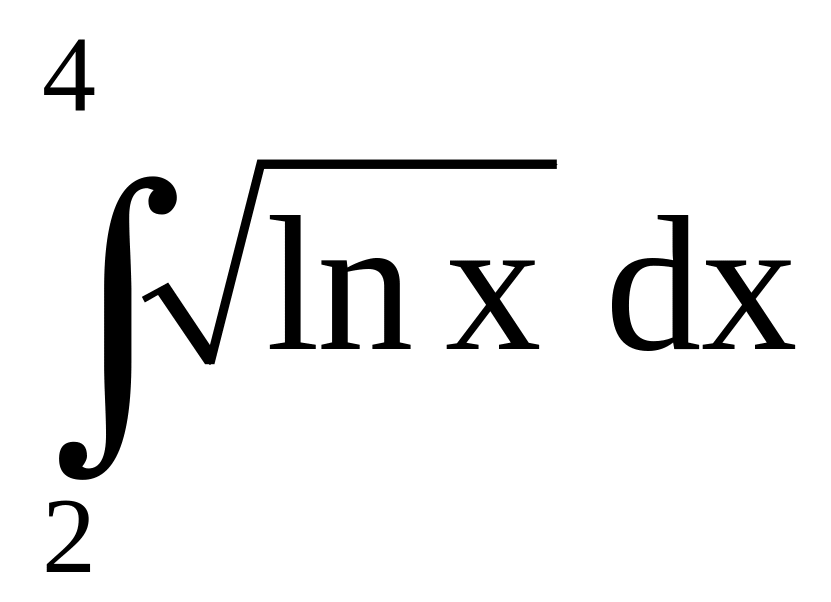методами:

а) прямоугольников, б) трапеций, в) Симпсона, взяв . В методах прямоугольников и трапеций оценить погрешность вычисления.

Решение. а) Составим таблицу .

xк	2	2,2	2,4	2,6	2,8
yк	0,8326	0,8880	0,9357	0,9775	1,0147

xк	3	3,2	3,4	3,6	3,8
yк	1,0481	1,0785	1,1062	1,1318	1,1554

Воспользуемся первой из формул прямоугольников

0,2(0,8326 + 0,8880 + 0,9357 + 0,9775 + 1,0147 + 1,0481 + + 1,0785 + 1,1062 + 1,1318 + 1,1554) = 0,210,1685 = 2,0337.

Оценим погрешность 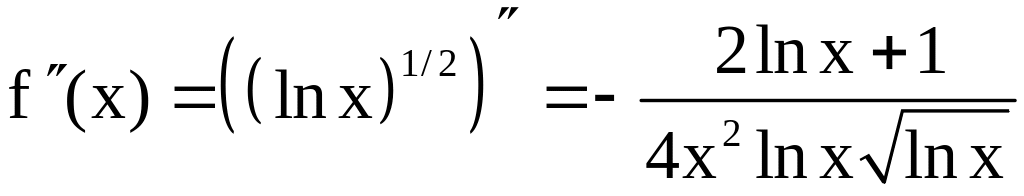. Нетрудно видеть, что .

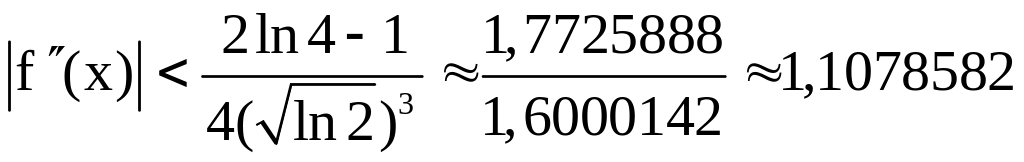Отсюда и погрешность не превышает .

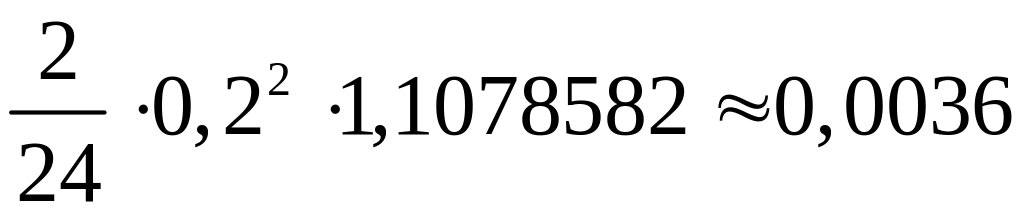б) Для применения формулы трапеций дополним выше составленную таблицу ещё одним значением: . Имеем

.

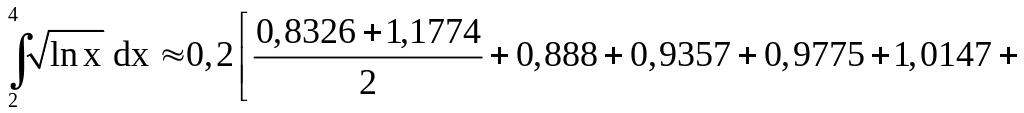
Погрешность вычисления равна .

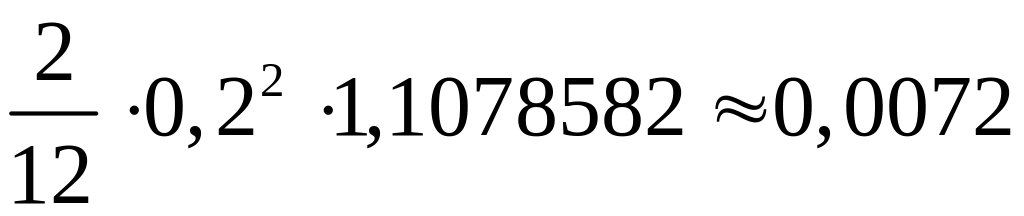в) Рассмотрим нашу таблицу (h = 0,1).

xк	2	2,1	2,2	2,3	2,4
yк	0,832555	0,861358	0,887951	0,912639	0,935665
xк	2,5	2,6	2,7	2,8	2,9
yк	0,957231	0,977503	0,996620	1,014702	1,031848
xк	3	3,1	3,2	3,3	3,4
yк	1,048147	1,063674	1,078495	1,092668	1,106244
xк	3,5	3,6	3,7	3,8	3,9
yк	1,119269	1,131784	1,143824	1,1554224	1,166609
xк	4
yк	1,177410

Отсюда находим

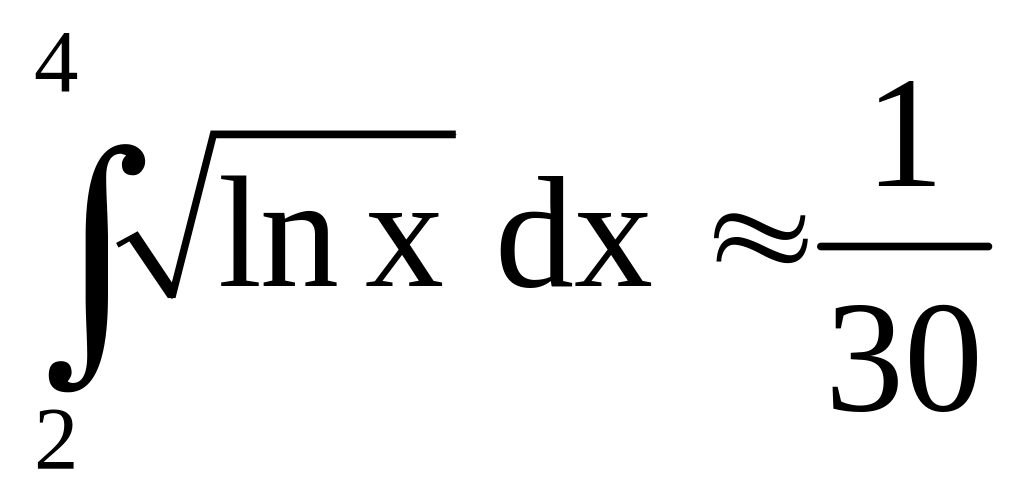[(0,832555 + 1,17741) + 4(0,861358 + 0,912639 +

+0,957231 + 0,99662 + 1,031848 + 1,063674 + 1,092668 + 1,119269 + +1,143824 + 1,166609) + 2(0,887951 + 0,935665 + 0,977503 + 1,014702 + +1,048147 +1,078495 +1,106244 + 1,131784 +1,155422)] = 62,064751  2,068825  2,0688.