Лекция № 8

Тема: «Устойчивость тонкостенных оболочек»

Элементы тонкостенных конструкций (стержни, пластины, оболочки) могут разрушаться в результате потери устойчивости. Под потерей устойчивости следует понимать резкое качественное изменение характера деформации элемента конструкции, происходящее при определенном значении нагрузки.

Обычно упругая система, потерявшая устойчивость, переходит к некоторому новому положению устойчивого равновесия, отличающемуся от первоначального. Этот переход в подавляющем большинстве случаев сопровождается существенными перемещениями, нарушающими возможность нормальной эксплуатации конструкции в связи с возникновением больших деформаций или приводящими к полному разрушению конструкции. При потере устойчивости тонкостенной конструкции нормальные и касательные напряжения в её поперечных сечениях могут быть значительно ниже предела текучести.

Нагрузку, при которой происходит потеря устойчивости, называют критической. Например, прямолинейная форма равновесия сжатого стержня устойчива только в том случае, когда сжимающая стержень сила меньше критической. При силе большей критической стержень изгибается, прямолинейная форма равновесия перестаёт быть устойчивой. При этом круговая форма её поперечного сечения может перейти, например, в эллиптическую, и оболочка сплющивается, хотя напряжения в стенках оболочки могут быть меньше предела текучести. Цилиндрическая оболочка может потерять устойчивость при осевом сжатии, кручении, поперечном изгибе и т. д.

Следует отметить, что потеря устойчивости происходит в основном из-за неизбежных начальных неправильностей в срединной поверхности оболочек (отклонений геометрической формы конструкции от идеальной).

Очень тонкие оболочки могут потерять устойчивость скачкообразно, с так называемым «прощёлкиванием», в этом случае новое равновесное состояние может быть сохранено при незначительной величине внешней нагрузки. Это равновесное состояние достигается при больших прогибах оболочки. Критическая нагрузка, соответствующая этой форме потери устойчивости, является наименьшей из возможных и определяет нижний предел устойчивости.

Величина критической нагрузки (или критического напряжения) зависит также от условий закрепления конструкции, соотношения её размеров (например, для цилиндрических оболочек от отношений ), вида действующей нагрузки и т. д.

Рассмотрим замкнутую круговую цилиндрическую оболочку длиной L, шарнирно опёртую по торцам (рис. 18). Пусть оболочка подвергается сжатию вдоль образующей усилиями N₁, Равномерно распределёнными вдоль дуговых кромок.

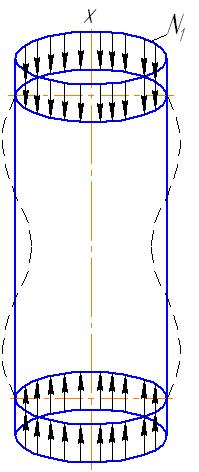
Рис. 18. Схема замкнутой круговой цилиндрической оболочки длиной L, шарнирно опёртую по торцам

Предположим, что поверхность оболочки остаётся осесимметричной и после выпучивания, которое имеет волнообразный характер. Тогда радиальные прогибы у оболочки будут зависеть только от координаты Х, совпадающей с осью оболочки и характеризующей положение данного нормального сечения. Критическое напряжение в стенке оболочки определяют из условия равновесия внутренних усилий оболочки в момент потери устойчивости, когда появляется новая форма равновесия, отличная от первоначальной – прямолинейной.

Напряжённое состояние оболочки при потере устойчивости из безмоментного превращается в моментное и, следовательно, претерпевает качественный скачок.

Оболочка подвергается изгибу под действием постоянных сил сжатия N₁, а не поперечной нагрузки.

При выпучивании эти силы дают нормальную составляющую:

,

где у – радиальный прогиб оболочки.

Общее выражение для определения прогиба:

, (3)

где D – цилиндрическая жёсткость оболочки .

Вводя в уравнение (3) в качестве дополнительной поперечной нагрузки указанную нормальную составляющую, можно записать:

. (4)

Принимаем выражение для прогиба:

, (5)

где m – число полуволн изогнутой поверхности по образующей оболочки; L – длина оболочки.

На основании выражений (4) и (5) получим выражение для верхнего критического напряжения

.

Исследуя это выражение на минимум, получим значение m, соответствующее минимальному критическому напряжению:

. (6)

Тогда действительное значение верхнего критического напряжения

, (7)

при μ = 0,3

.

Аналогичный результат получается и при допущении, что поверхность оболочки после выпучивания не остаётся осесимметричной. Экспериментальные данные свидетельствуют о том, что найденное критическое значение сжимающих напряжений является верхней границей для действительных критических напряжений.

При нетщательном изготовлении оболочки, когда начальные прогибы приближаются по величине к толщине стенки h, что является пределом допустимых начальных прогибов, расчётные значения критических напряжений следует уменьшать почти в 2 раза.

Исследуем задачу об устойчивости кольца, сжатого радиальной равномерно распределённой нагрузкой интенсивностью q. Предположим, что кольцо при некотором значении внешней нагрузки теряет свою форму и сплющивается (рис. 19а).

Рассмотрим элемент деформированного кольца (рис. 19б) длиной ds; местный радиус кривизны элемента оболочки обозначим через ρ. Предположим, что радиус кривизны ρ близок по величине к первоначальному радиусу R. На концах элемента действуют нормальные силы, поперечные силы и изгибающие моменты.

Обозначим нормальную силу до потери устойчивости N0, а после потери устойчивости N₀ + N.

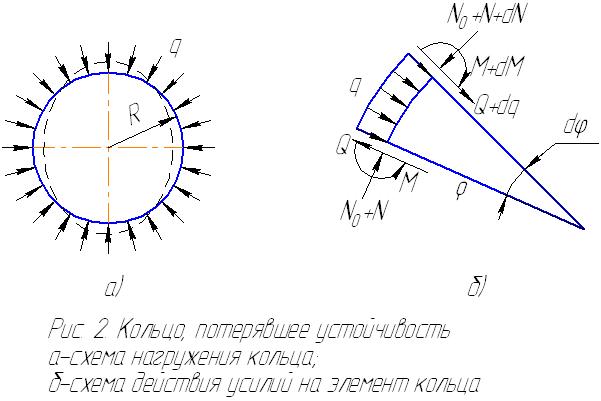
Рис. 19. Кольцо, потерявшее устойчивость: а – схема нагруженного кольца; б – схема действия усилий на элемент кольца

Для докритического состояния из условия равновесия следует

,

откуда .

Сумма проекций на нормаль сил, действующих на элемент:

Подставим сюда полученное значение N₀ , учитывая что ρ ≈ R:

, (8)

где – изменение кривизны.

Запишем ещё 2 уравнения равновесия

(9)

(10)

Решением уравнений (8), (9), (10) получается уравнение

. (11)

После интегрирования (11) можем определить q_кр

.

Минимальное значение q_кр получают при n = 2, когда

.

Результаты, полученные для кольца, можно использовать для расчёта длинных цилиндрических оболочек, нагруженных внешним давлением р. При этом q = р; вместо величины жёсткости EI следует использовать величину цилиндрической жёсткости оболочки:

.

Тогда .