Лекция № 3

Тема: «Безмоментная теория (мембранная теория оболочек)»

Выделим из рассматриваемой оболочки (рис. 4) элемент поверхности двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану. Обозначим радиусы кривизны дуги меридиана и сечения, перпендикулярного к дуге меридиана, через ρ_m и ρ_t, толщину стенки через s и размеры элемента в меридиональном и окружном (кольцевом) направлениях через dS_m и dS_t. На гранях элемента возникают напряжения σ_m и σ_t. Первое напряжение σ_m называют меридиональным напряжением. Второе напряжение σ_t называют окружным или кольцевым.

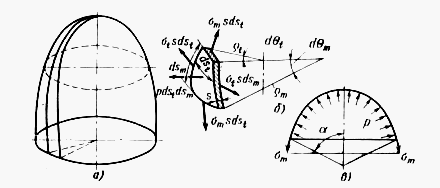
Рис. 4. Схема к определению мембранных напряжений в оболочке: а – оболочка; б – элемент стенки; в – часть оболочки

Напряжения σ_m и σ_t, умноженные на соответствующие площади граней элемента дадут силы σ_msds_t и σ_tsds_m, (рис. 5). Равнодействующая этих сил в направлении, нормальном к поверхности элемента:

.

Равнодействующая усилий σ_mds_ts в направлении, нормальном к поверхности элемента, будет σ_mds_tsds_m/ρ_m.

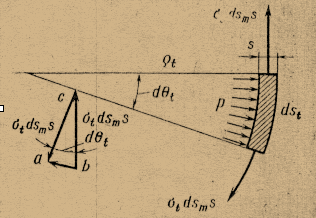
Рис. 6. Схема действия усилий на элемент оболочки

Сумма этих равнодействующих уравновешивает силу, действующую по нормали к поверхности элемента, приложенное к элементу:

,

откуда

.

Полученное уравнение называют уравнением Лапласа. Этого уравнения недостаточно для определения двух функций напряжения σ_m и σ_t. Для получения второго уравнения отсечем коническим нормальным к меридиану сечением часть оболочки (рис. 5в) и отбросим нижнюю часть. Действие отсеченных стенок заменим действующим в меридиональном направлении упругими силами:

.

Из вышеуказанных двух уравнений находим:

, .

Для цилиндрического сосуда ρ_t = r (где r – радиус сосуда), ρ_m = ∞, итак

, .

Для конического сосуда радиус кривизны окружного сечения ρ_t = r_K/cos α, где r_K – радиус основания конической оболочки; α – половина угла конуса:

, .

Сопоставляя полученные формулы для цилиндрического и конического сосуда, легко увидеть, что при одинаковом давлении, диаметрах сосудов и толщине стенок максимальное нормальное напряжение сферической оболочки в два раза меньше нормального напряжения цилиндрической, а конической больше в 1/cos α.

Применение безмоментной теории для конических оболочек.

Коническим чаще всего бывают днища. Применяются такие днища в вертикальных аппаратах при условии, если необходим слив продукта и последующая его очистка. Они наиболее громоздки и технологически получаются с помощью вальцовки, при которой производится отбортовка. Иногда применяются конические переходы.

Рассмотрим цилиндрический аппарат с коническим днищем.

Внутреннее давление Р.

Напряжение переменное.

ρ_m→∞

Тогда

;

;

;

;

;

.

Из уравнения Ла-Пласса: ρ_m→∞, тогда:

;

.

Для нахождения выражений напряжений σ_m и σ_t необходимо:

– составить уравнение равновесия элемента оболочки;

– составить уравнение равновесия рассматриваемой зоны (без отсечённой зоны).

Лекция № 4

Тема лекции: «Моментная теория оболочек»

Рассмотрим тонкостенный цилиндр радиуса R и постоянной толщины h, который находится под действием некоторой осесимметричной нагрузки (рис. 6).

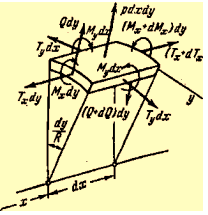
Рис. 6. Элемент тонкостенного цилиндра

Обратимся к уравнениям равновесия элемента оболочки с размерами h, dx = R₁dφ, dy = R₂ sin φd α (здесь sin φ = 1, т. к. φ = π/2) и приложим к его граням равнодействующие силы и моменты, величины которых равны S, T, М и K, умноженным соответственно на dy = R₂ sin φd α и dx = R₁sin φ. Кроме четырех перечисленных силовых факторов, прикладываем также поперечную силу NR₂sin φ d α. Внешние силы характеризуются постоянным давлением, т. е. р = const. Поскольку ни внешняя нагрузка, ни радиусы кривизны оболочки не меняются вдоль ее оси, dNR₂sin φ =0, т. е. ds = const.

Это значит, что осевая сила определяется условиями нагружения цилиндра на торцах. Уравнение равновесия на ось z примет вид:

или .

Наконец, третье уравнение равновесия получаем, приравнивая к нулю сумму моментов всех сил относительно оси y:

, откуда .

Деформации и напряжения, возникающие в оболочке, также обладают, очевидно, осевой симметрией, и деформированный цилиндр представляет собой некое тело вращения. Форма этого тела вполне определяется формой изогнутой образующей цилиндра.

Обозначим через ω радиальное перемещение, а через ν – угол наклона касательной к образующей срединной поверхности цилиндра (рис. 7). При этом, естественно:

.

Перемещение ω будем отсчитывать наружу, т. е. от оси цилиндра.

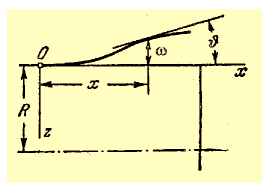
Рис. 7. Искривление образующей цилиндра

Относительное удлинение ε_х отрезка АВ (рис. 8), расположенного на расстоянии z от срединой поверхности, складывается из двух составляющих: из удлинения ε₀ срединой поверхности и удлинения, обусловленного искривлением образующей цилиндра.

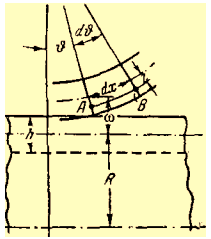
Рис. 8.

Последнее слагаемое имеет вид:

.

Полное удлинение слоя АВ будет составлять:

.

Удлинение в окружном направлении:

.

Эти удлинениям соответствуют напряжения σ_s и σ_t, определяемую по закону Гука:

, .

где μ – коэффициент Пуассона. Согласно выражению полного удлинения слоя перепишем найденные напряжения:

,

.

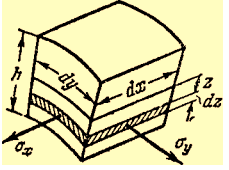
Рис. 9. Элемент оболочки с размерами dxdy

Нормальные силы в площадках hdy и hdx, отнесенные к единице длины сечения элемента, будут иметь вид

, .

Определим в этих же сечениях изгибающие моменты:

, .

, ,

, ,

где .

Теперь исключим изгибающий момент М и Т, а также ε₀, получим уравнение относительно одного неизвестного – перемещения ω:

,

где , k = 1,28/(Rh)^1/2 – характеристический коэффициент.

Решение уравнения перемещения имеет вид:

. (2)

В этом уравнении С₁, С₂, С₃ и С₄ – постоянные интегрирования, ω₀ – частное решение уравнения одного неизвестного перемещения при р = const.

.

Постоянные интегрирования определяются из граничных условий на концах оболочки. Например, в случае если длина оболочки l > S(Rh)^1/2, то как показывают исследования, прогибы и напряжения у одного края мало влияют на прогибы и напряжения у другого края. Поэтому для такой оболочки следует принять С₃ = С₄ = 0, т. к. иначе при увеличении х прогиб будет возрастать неограниченно. В результате уравнение (2) будет иметь вид:

.

Зная уравнение для прогиба, можно определить действующие в оболочке усилия и моменты из следующих соотношений:

; ; ; .

Наибольшие изгибающие моменты и напряжения возникают в месте заделки оболочки (х = 0):

; ; ; .

На рис. 10 представлены эпюры меридиональных моментов и радиальных перемещений жестко защемленной оболочки, нагруженной внутренним давлением.

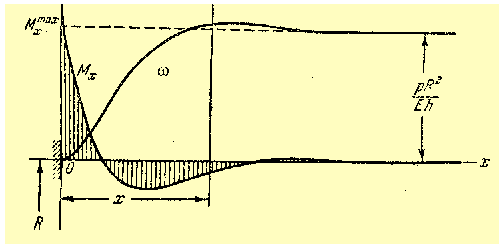
Рис. 10. Эпюры меридиональных моментов и радиальных перемещений жесткозащемленной оболочки

Нетрудно видеть, что зависимость М = М(х) представляет собой периодическую, быстро затухающую функцию. Очевидно, что анологично изменяется по длине оболочки и кольцевой момент.

Итак, первый важный вывод, который вытекает из моментной теории оболочек, состоит в том, что изгибающий кольцевой и меридиональный моменты в нагруженной осесимметрично цилиндрической оболочке затухают очень быстро, и уже на расстоянии l = 2,7(Rh)^1/2 величиной их можно пренебречь. Примерно такова же область действия изгибающих моментов в других видах оболочек.

Другой вывод, заключается в том, что моментная теория оболочек позволяет рассчитать прогибы и углы поворота на концах оболочки, нагруженных единичным изгибающим моментом М₀ = 1 и единичной перерезывающей силой Q₀ = 1.

Обозначим:δ_мм – угол поворота края оболочки от действия на него момента М₀ = 1; δ_мQ – угол поворота края оболочки от действия на краю поперечной силы Q₀ = 1; δ_QQ – прогиб края оболочки от действия на краю поперечной силы Q₀ = 1; δ_QМ – прогиб края оболочки от действия на краю момента М₀ = 1.

Коэффициенты δ_мQ и δ_QМ симметричны, т. е. δ_мQ = δ_QМ. Значения коэффициентов для определения единичных перемещений наиболее распространенных в практике аппаратостроения оболочек приведены в табл. 2 [6].

Таблица 2