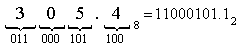Перевод чисел из одной системы счисления в другую
Теоретическая часть
Перевод чисел в десятичную систему из любой ПСС осуществляется путем представления числа в виде полинома (формула 2.1) и вычислением полученной суммы.
Пример 3.1. Осуществить перевод чисел в десятичную СС (таблица 3.1):
а) 10101101.1012
( ? )10 ;
б) 703.048
( ? )10;
в) B2E.416
( ? )10.
Таблица 3.1 – Порядок выполнения переводов чисел в ПСС
а) 10101101.1012 ( ? )10 |
1 0 1 0 1 1 0 1 . 1 0 1 = 1 * 27 + 0 * 26 + 1 * 25 + 0 * 24 + 1 * 23 + 1 * 22 + 0 * 21 + 7 6 5 4 3 2 1 0 -1 -2 -3 + 1 * 20 + 1 * 2-1 + 0 * 2-2 + 1 * 2-3 = 173 . 625 |
б) 703.048 ( ? )10 |
7
0
3
.
0
4
=
7 2 1 0 -1 -2 |
в) B2E.416 ( ? )10 |
B 2 E . 4 = 11 162 + 2 161+ 14 160+ 4 16-1 =2862.25 2 1 0 -1 |
82+
0
81+
3
80+
0
8-1+
4
8-2
=
451.0625
Для перевода десятичного вещественного числа в любую ПСС необходимо:
– выделить в десятичном числе целую и дробную части;
– целую часть десятичного числа делить на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде последовательности: частное, далее остатки деления, начиная с последнего;
– дробную часть числа необходимо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части, находящиеся за запятой. Умножение прекращается, как только после десятичной точки появится ноль. Дробная часть в новой системе записывается в виде последовательности цифр стоящих перед десятичной точкой, начиная с первой верхней. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности;
–
в
любой СС целая часть числа при переводе
остается целой, а дробная – дробной.
Поэтому для получения конечного
результата целая и дробная части,
полученные в результате перевода,
соединяются.
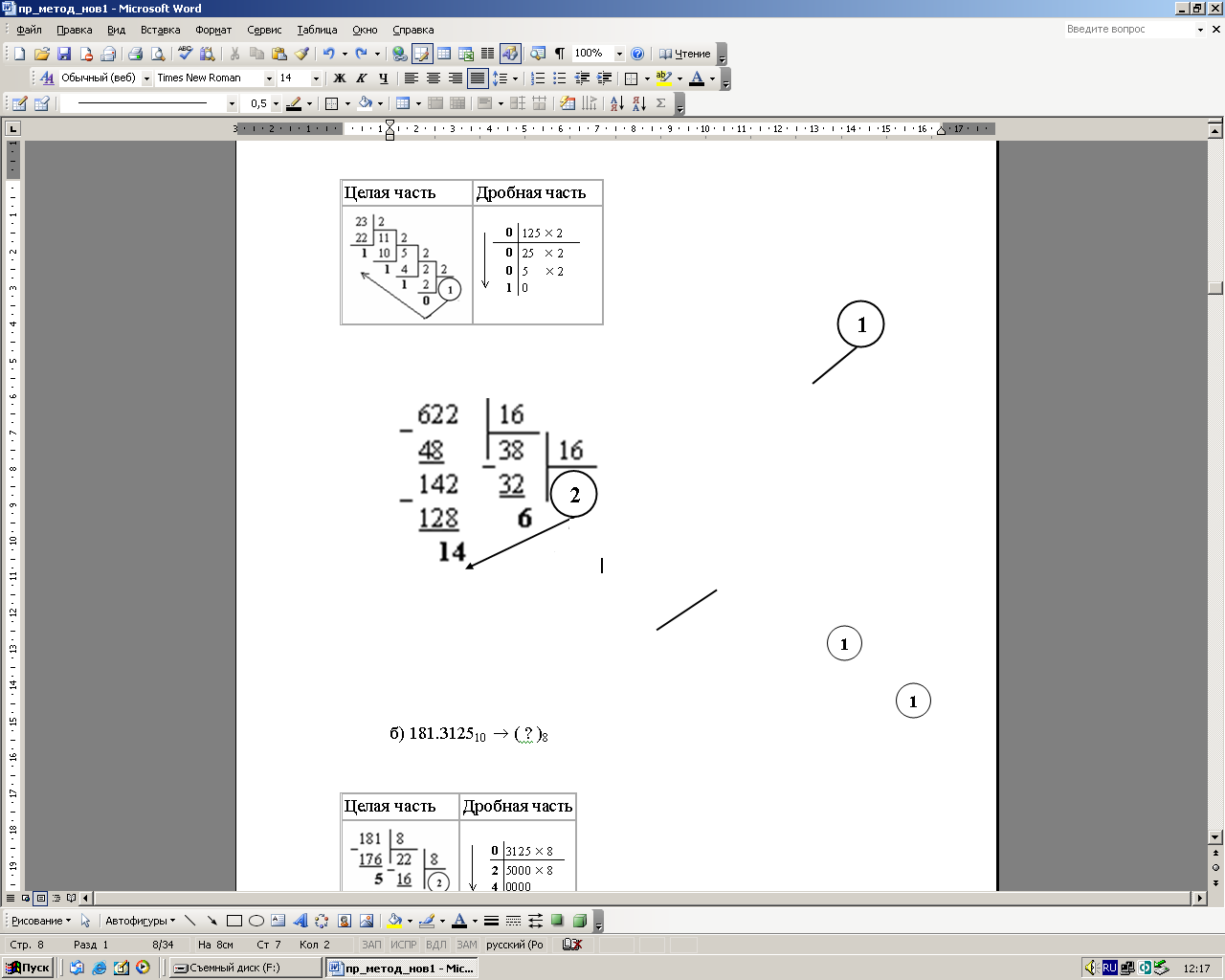
Пример 3.2. Осуществить перевод чисел представленных в десятичной системе (таблица 3.2):
а) 23.12510 ( ? )20; б) 181.312510 ( ? )8; в) 622.6510 ( ? )16..
Таблица 3.2 – Порядок выполнения переводов чисел в ПСС
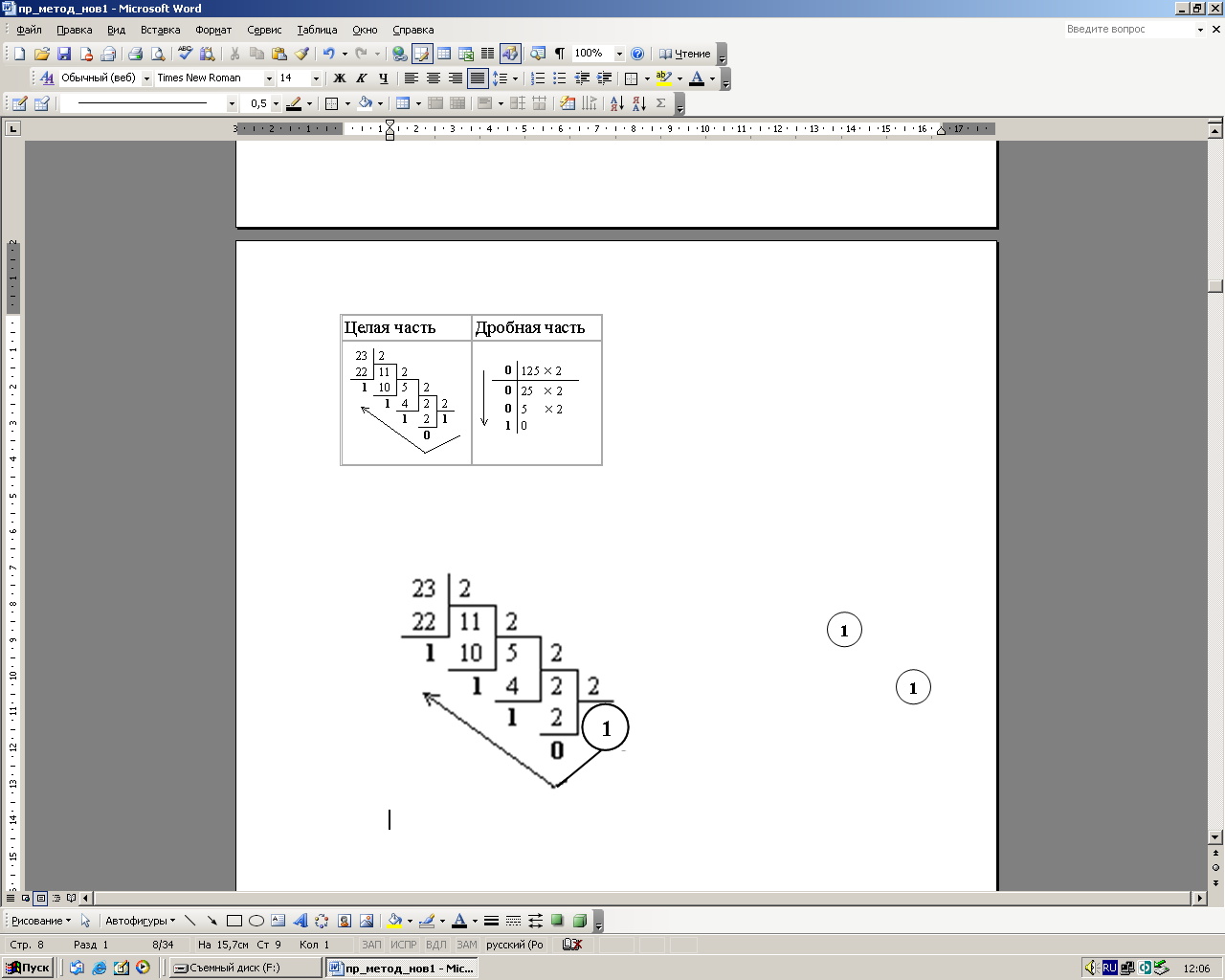
а) 23.12510 ( ? )2 |
||
Целая часть – 23 |
Дробная часть – 125 |
Пояснения |
|
|
2310 = 101112; 0.12510 = 0.0012.
23.12510 = 10111.0012. |
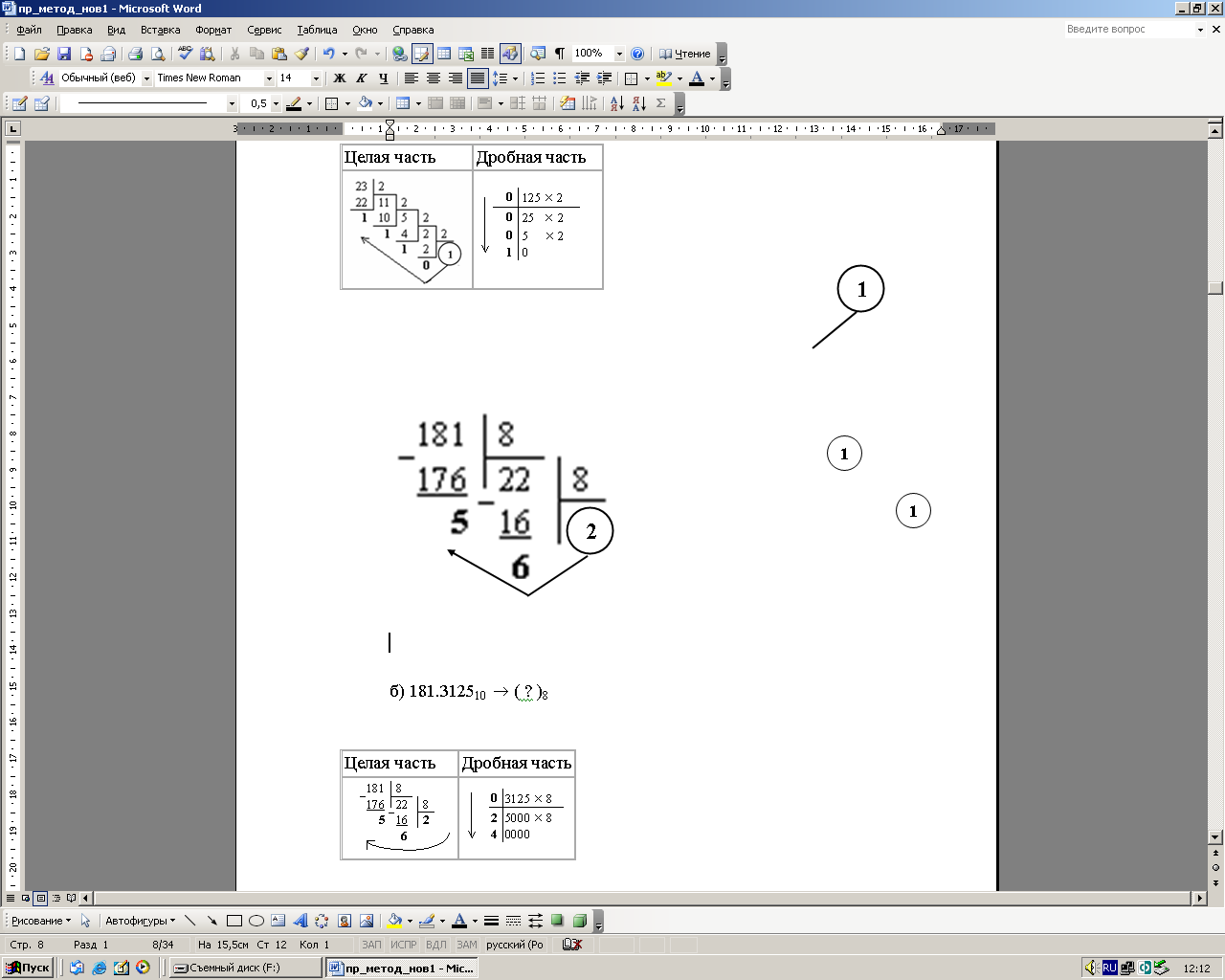
б) 181.312510 ( ? )8 |
||
Целая часть – 181 |
Дробная часть – 3125 |
Пояснения |
|
, 3125 * 8
4, 0
|
181.312510 = 265.248
|
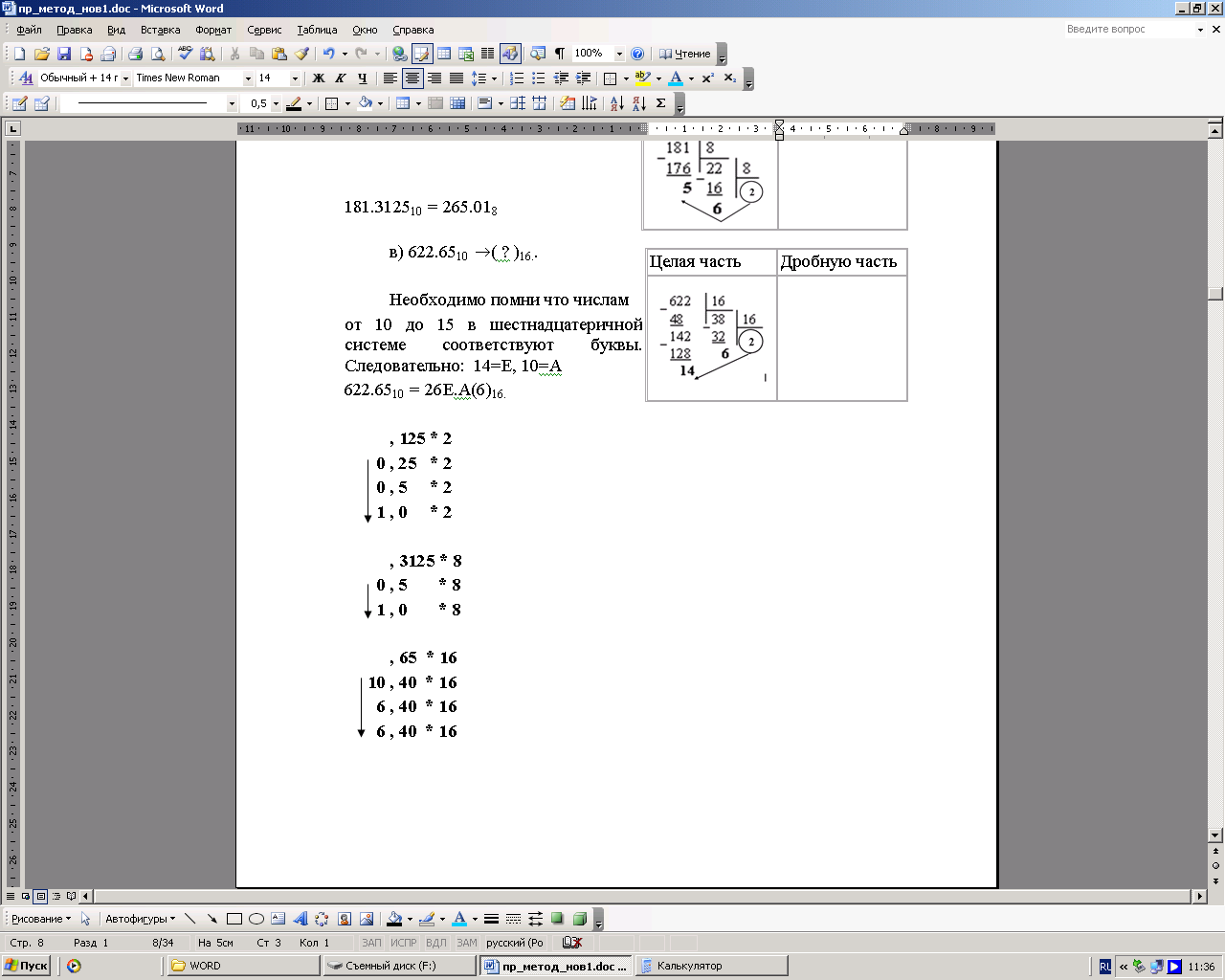
в) 622.6510 ( ? )16. |
||
Целая часть – 622 |
Дробная часть – 65 |
Пояснения |
|
|
Числам от 10 до 15 в шестнадцатеричной СС соответствуют буквы. Т.е. 14=Е, 10=А.
622.6510 = 26Е.А(6)16. |
2, 5 *8
Перевод восьмеричного числа в двоичную ПСС достаточно заменить каждую цифру соответствующим двоичным числом (таблица 2.1) и записать его в виде трехразрядного числа (триады). Например, цифра 2 в двоичной системе – 10, 10 в виде триады – 010; цифра 7 в двоичной системе – 111, 111 в виде триады – 111. Ненужные нули в старших и младших разрядах результата можно отбрасывать..
Перевод шестнадцатиричного числа в двоичную ПСС производится аналогично. Двоичное число записывается в виде четырехразрядного числа (тетрады). Например, цифра 1 в двоичной системе – 1, 1 в виде тетрады – 0001; цифра 7 в двоичной системе – 111, 111 в виде тетрады – 0111.
Пример 3.3. Осуществить перевод:
Таблица 3.3 – Порядок выполнения переводов чисел в ПСС
а) 305.48 ( ? )2 |
б) 7B2.E16 ( ? )2 |
|
|
а ) 305.48 ( ? )2
305.48 = 11000101.12
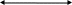
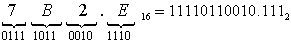
7B2.E16 = 11110110010.1112
Для перевода двоичного числа в восьмеричную (шестнадцатеричную) СС поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
П
ример
3.4. Осуществить
перевод:
а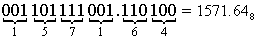
)
1101111001.11012
( ? )8
1101111001.11012 = 1571.648
б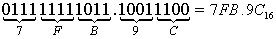
)
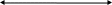
11111111011.1001112
( ? )16
11111111011.1001112 = 7FB.9C16
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример 3.5. Осуществить перевод:
175.248 ( ? )16
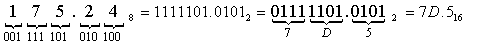
175.248 = 7D.516.
Задания
1. Осуществить перевод чисел в десятичную СС:
а) 10110111.10112; б) 563.448; в) 1C4.A16.
2. Осуществить перевод десятичных чисел в двоичную, восьмиричную и шестнадцатиричную СС: а) 120.625; б) 362,25.
3. Перевести числа в указанную СС:
а) 11011001.010112 ( ? )8; б) 1101111101.01011012 ( ? )16.
в) 312.78 ( ? )16; г) 5B.F16 ( ? )8.
4. Перевести числа в двоичную СС:
а) 1725.3268; б) 7BF.52A16.