11.1.2. Свободные гармонические колебания в объемных резонаторах

 

Предположим, что в объеме V_o (в произвольном резонаторе) тепловые потери равны нулю и, кроме того, отсутствует обмен энергией между внешним пространством и внутренним объемом резонатора. Уравнение баланса (1.126) при этих условиях име­ет вид

 

Р^ст =dWldt.                                (11.1)

 

Под влиянием источника в объеме V_o возникнут электромаг­нитные колебания. Пусть через некоторое время сторонний источ­ник отключается. При этом за счет запасенной в резонаторе энер­гии колебательный процесс будет продолжаться сколь угодно дол­го и при отсутствии источников. В резонаторе возникнут свободные или, другими словами, не связанные со сторонним источником электромагнитные колебания. При Р^ст = 0 из (11.1) получаем

 

dWdf = O,                                       (11.2)

 

т.е. в соответствии с законом сохранения энергии полная энергия, запасенная в изолированном от внешнего пространства объеме, при отсутствии потерь в любой момент времени остается постоян­ной. Однако соотношение величин электрической и магнитной энергий в общей неизменной сумме непрерывно меняется ввиду обмена энергией между переменными электрическим и магнитным полями. В общем случае изменение во времени напряженности электрических и магнитных полей в резонаторе носит негармони­ческий характер. Особый интерес представляет случай, когда свободные колебания являются гармоническими. Пусть, например, Е = Ei sin ω_ot, где E₁ - функция, зависящая от пространственных координат, а ω_о - угловая частота свободных колебаний. В момент t = 0 напряженность электрического поля равна нулю. Равна нулю в этот момент и энергия, запасенная в электрическом поле. Но полная энергия в объеме V_o резонатора, как следует из (11.2), не зависит от времени. Следовательно, в момент t = 0 у рассматри­ваемого свободного колебания вся энергия сосредоточена в маг­нитном поле, что при гармонических колебаниях означает наличие фазового сдвига, равного π/2, между векторами Е и Н, т.е. Н = H₁ cos ω_ot, где Н₁ - функция пространственных координат. Пе­реписывая (11.2) для гармонических колебаний с учетом формул (1.130)-( 1.132), получаем

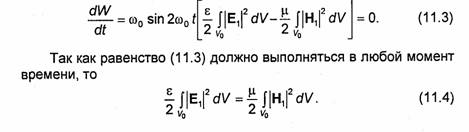
11.1.3. Резонансные частоты свободных колебаний

 

В рассматриваемом случае уравнения Максвелла (1.33) и (1.39) можно переписать в виде

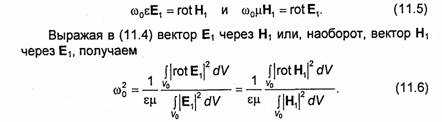
Слева в (11.6) стоит квадрат резонансной угловой частоты объемного резонатора, а справа - всегда положительная вели­чина, равная отношению двух объемных интегралов. Численное значение каждого из этих интегралов зависит от формы объема Vo и его размеров, а также от характера подынтегральной функции. Поэтому резонансная частота резонатора зависит от структуры попей в резонаторе, его формы и размеров.

Структура полей в резонаторе, как и в направляющих сис­темах, определяется путем решения уравнений Максвелла при определенных граничных условиях на поверхности, окружающей объем V_o. В случае закрытых резонаторов без потерь задача сво­дится к решению трехмерного векторного волнового уравнения:

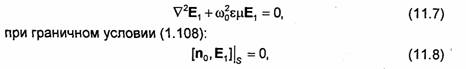
где S - внутренняя поверхность металлической оболочки резона­тора, а n₀ - орт нормали к этой поверхности.

Можно доказать, что уравнение (11.7) при граничном условии (11.8), как и аналогичные уравнения теории направляющих систем, имеет бесконечное число различных решений, каждому из которых согласно (11.6) соответствует определенное значение резонан­сной угловой частоты ω₀, т.е. объемные резонаторы, в отличие от обычных контуров из сосредоточенных элементов, резонируют не на одной частоте, а на бесконечном множестве дискретных частот ωo₁, ω₀₂.....ω_0p.....То колебание, которому при данных размерах резонатора соответствует минимальная резонансная частота ω_О1, называют низшим колебанием. Отметим, что каждой резонансной частоте соответствует определенная структура электромагнитного поля в резонаторе.

.