
- •Раздел 1. Элементы линейной алгебры и аналитической геометрии
- •Глава 1. Матрицы и определители
- •1.1.Понятие матрицы
- •1.2. Основные операции над матрицами
- •1.3. Определители второго и третьего порядка
- •1.4. Определитель n-го порядка
- •1.5. Основные свойства определителей.
- •1.6. Алгебраические дополнения.
- •1.7. Ранг матрицы.
- •1.8. Обратная матрица.
- •Глава 2. Системы линейных алгебраических уравнений (слау)
- •2.1. Основные понятия и определения.
- •2.2. Условие совместимости слау. Теорема Кронекера-Капелли
- •2.3. Правило Крамера решения слау
- •2.4. Метод Гаусса
- •2.5. Решение произвольных слау
- •2.6. Системы однородных уравнений
- •2.7. Матричные уравнения
- •Глава 3. Векторы
- •3.1. Понятие вектора. Линейные операции над векторами
- •3.2. Линейно зависимые и линейно независимые векторы. Базис
- •3.3. Скалярное произведение векторов
- •3.4. Векторное произведение векторов
- •3.5. Смешанное произведение трех векторов
- •Глава 4. Аналитическая геометрия
- •4.1. Общее уравнение прямой на плоскости
- •4.2. Уравнение прямой, проходящей через две точки. Угол между прямыми
- •4.3. Нормальное уравнение прямой. Расстояние от точки до прямой
- •4.4. Общее уравнение плоскости. Неполные уравнения плоскости. Уравнение плоскости в отрезках
- •4.5. Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •4.6. Уравнение плоскости, проходящей через 3 данных точки. Угол между плоскостями
- •4.7. Прямая в пространстве
- •4.8. Взаимное расположение прямой и плоскости в пространстве
- •4.9. Окружность
- •4.10. Эллипс
- •4.11. Гипербола
- •4.12. Парабола
- •Раздел II. Введение в математический анализ
- •Глава 5. Функции
- •5.1. Понятие множества. Логическая символика
- •5.2. Понятие функции. Основные свойства функции
- •5.3. Основные элементарные функции
- •5.4. Элементарные функции. Классификация функций.
- •Глава 6. Пределы и непрерывность
- •6.1. Предел числовой последовательности
- •6.2. Предел функции в бесконечности и в точке
- •6.3. Бесконечно малые величины
- •6.4. Бесконечно большие величины
- •6.5. Основные теоремы о пределах
- •6.6. Признаки существования предела
- •6.7. Первый замечательный предел
- •6.8. Второй замечательный предел
- •6.9. Непрерывность функции в точке и на промежутке
- •6.10.Классификация точек разрыва
- •Раздел III. Дифференциальное исчисление
- •Глава 7. Производная и дифференциал
- •7.1. Физический и геометрический смысл производной
- •7.2. Определение производной. Свойства
- •7.3. Производная сложной и обратной функций
- •7.4. Производные тригонометрических функций
- •7.5. Производная обратных тригонометрических функций
- •7.6. Производная показательной, логарифмической и степенной функций
- •7.7. Производная гиперболических функций
- •7.8. Логарифмическая производная. Производная неявной и параметрической функции
- •7.9. Дифференциал функции
- •7.10. Производные и дифференциалы высших порядков
- •Глава 8. Основные теоремы дифференциального исчисления
- •8.1. Теорема Ферма
- •8.2. Теорема Ролля
- •8.3. Теорема Лагранжа
- •8.4. Теорема Коши
- •8.5. Правило Лопиталя
- •8.6. Формулы Тейлора и Маклорена
- •Глава 9. Приложения производной
- •9.1. Интервалы монотонности. Признаки экстремума
- •9.2. Выпуклость и вогнутость. Точки перегиба
- •9.3. Асимптоты графика функции
3.2. Линейно зависимые и линейно независимые векторы. Базис
Линейная комбинация векторов. Пусть
даны векторы
![]() .
Тогда всякий вектор, имеющий вид
.
Тогда всякий вектор, имеющий вид
![]() ,
где
,
где![]() – некоторые числа, называется линейной
комбинацией векторов
или вектор
– некоторые числа, называется линейной
комбинацией векторов
или вектор
![]() линейно выражается через векторы
.
линейно выражается через векторы
.
Данные векторы называются линейно-зависимыми, если какой-либо из этих векторов линейно выражается через остальные, в противном случае – эти векторы линейно независимые.
Два вектора линейно зависимы тогда
и только тогда, если они коллинеарны
друг другу. Из определения умножения
вектора на число следует: если
![]() ,
то
,
то
![]() .
Наоборот, если два вектора параллельны,
то любой из них можно растянуть во
столько раз, чтобы получить другой.
.
Наоборот, если два вектора параллельны,
то любой из них можно растянуть во
столько раз, чтобы получить другой.
Три вектора линейно зависимы тогда и только тогда, когда они компланарны (параллельны одной плоскости).
Доказательство:
Пусть
![]() .
Отнесем все три вектора
к одному началу и проведем через
и
.
Отнесем все три вектора
к одному началу и проведем через
и
![]() плоскость (Р). Тогда векторы
плоскость (Р). Тогда векторы
![]() и
и
![]() будут лежать в плоскости Р и их сумма
– вектор
тоже будет лежать в плоскости Р.
Значит,
компланарны плоскости Р.
будут лежать в плоскости Р и их сумма
– вектор
тоже будет лежать в плоскости Р.
Значит,
компланарны плоскости Р.
Наоборот, пусть параллельны плоскости Р. Если их отнести к одному началу, то все они будут лежать в плоскости Р. Если не параллелен , то можно представить в виде линейной комбинации и . Это разложение вектора в плоскости по двум некомпланарным векторам.

![]()
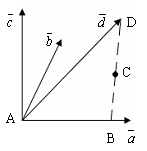
Четыре или более векторов всегда линейно зависимы.
Доказательство:
 Пусть
даны
Пусть
даны
![]() .
Отнесем их к одному началу. Если после
этого
лежат в одной плоскости, то они линейно
зависимы. Если
некомпланарны, то проведем через D
(конец
)
прямую, параллельно
до пересечения с плоскостью векторов
и
в точке С. Через С – прямую,
параллельную
.
Отнесем их к одному началу. Если после
этого
лежат в одной плоскости, то они линейно
зависимы. Если
некомпланарны, то проведем через D
(конец
)
прямую, параллельно
до пересечения с плоскостью векторов
и
в точке С. Через С – прямую,
параллельную
![]() до пересечения с прямой, на которой
лежит
до пересечения с прямой, на которой
лежит
![]() в точке В. Тогда
в точке В. Тогда
![]() – разложение вектора по трем
некомпланарным векторам (разложение
вектора по трем осям), что можно
осуществить единственным образом.
– разложение вектора по трем
некомпланарным векторам (разложение
вектора по трем осям), что можно
осуществить единственным образом.
Совокупность линейно независимых векторов, по которым производится разложение остальных векторов, называется базисом. В плоскости базисом могут служить два неколлинеарных вектора, в пространстве – три некомпланарных вектора.
Пусть
![]() –
базис,
–
произвольный вектор, тогда
–
базис,
–
произвольный вектор, тогда
![]() ,
где
,
где
![]() –координаты
вектора
в базисе векторов
.
–координаты
вектора
в базисе векторов
.
Обычно выбирают ортонормированный
базис, в котором векторы ортогональны
(перпендикулярны) и каждый вектор имеет
единичную длину. В этом случае базисные
векторы называют ортами и обозначают
![]() .
.
Декартовы координаты в пространстве
В качестве базиса декартовых координат
выбрали три вектора единичной длины
(орты), которые взаимно перпендикулярны
и отнесены к общему началу в точке О,
принятой за начало координат. Положение
произвольной точки М в пространстве
полностью характеризуется вектором
![]() ,
называемым радиус-вектором точки М.
,
называемым радиус-вектором точки М.
![]() ,
,
![]() -
декартовы координаты. Для любого вектора
-
декартовы координаты. Для любого вектора
![]() :
:
![]() ,
,
![]() -
проекции
на соответствующие оси.
-
проекции
на соответствующие оси.
Если
![]() ,
то
,
тогда
,
то
,
тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() – условие коллинеарности векторов.
– условие коллинеарности векторов.
Если
![]() ,
то
,
то
![]() или
или
![]() –
условие ортогональности векторов.
–
условие ортогональности векторов.
Направляющие косинусы вектора –
косинусы углов, которые он образует
с осями координат. Если
,
то
![]() ,
то есть
,
то есть
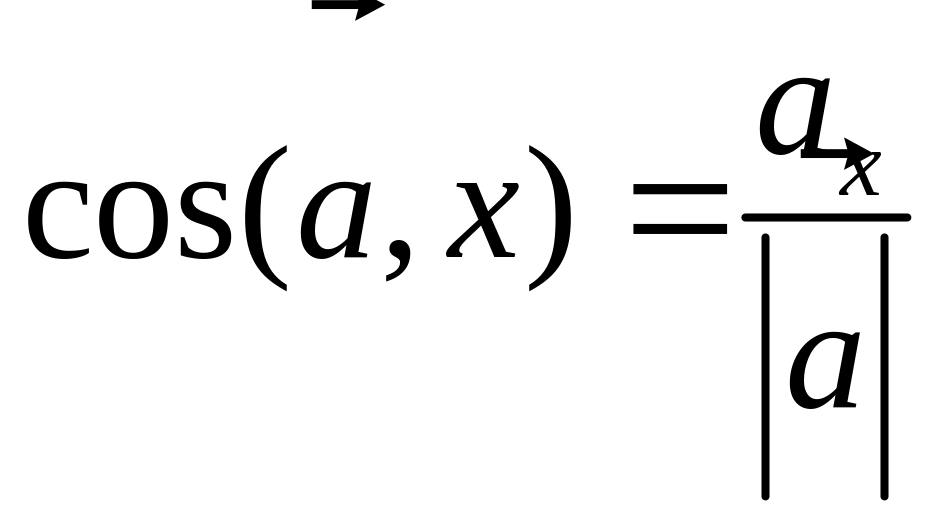 ,
,
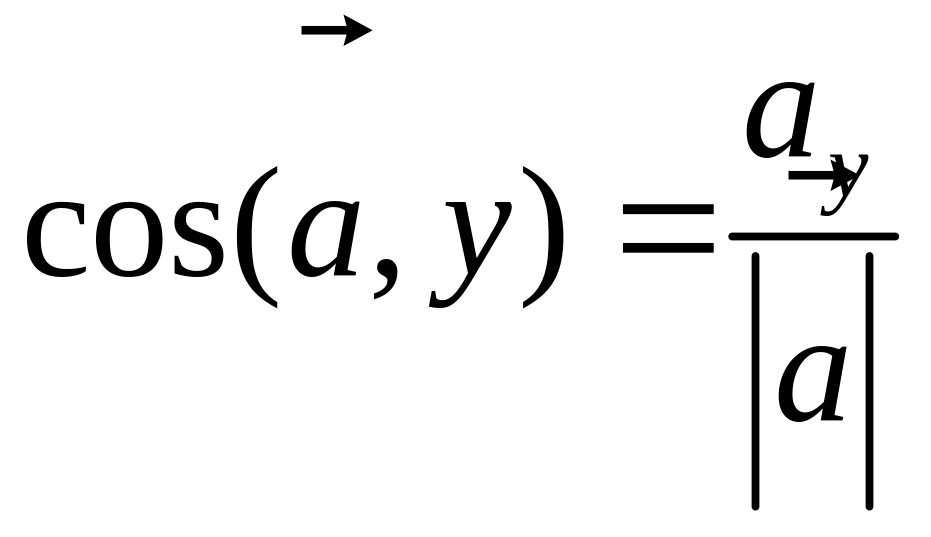 ,
,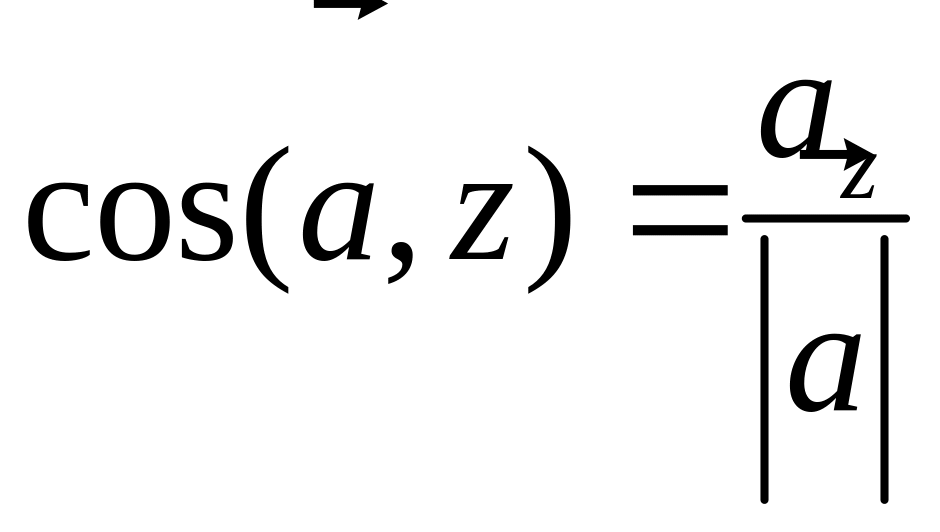 .
.
