7.8. Логарифмическая производная. Производная неявной и параметрической функции

Логарифмическая производная

Производная степенно-показательной функции

. Найдем ln y=φ(x) ln f(x). Дифференцируя, получим

= φ'(х) ln f(x) + φ (x)[1n f (x)]' = φ'(х) ln f (х) + .

Учитывая, что , получим после преобразований

.

Замечание. Производная логарифмической функции (ln y)’= называется логарифмической производной. Ее удобно использовать для нахождения производных функций, выражения которых существенно упрощаются при логарифмировании.

Пример 1. Вычислить .

Пример 2. .

Логарифмируем:

Производная неявной функции

Если задана неявная функция , то для вычисления производной надо взять производные от правой и левой частей, помня, что .

Например, .

.

Параметрическое задание функции

Пусть даны два уравнения .

Каждому значению t соответствует x и y на плоскости. Если , то эта точка описывает кривую на плоскости – кривая задана параметрически, t – параметр. , то .

Такое задание определяет , y от x задается параметрически. Используется в механике.

Производная. Ищем производную сложной функции:

- производная обратной функции.

Пример. . .

7.9. Дифференциал функции

Пусть и аргумент х получил приращение ∆х. Тогда дифференциалом называется величина , но , поэтому – отношение дифференциалов.

Вычисление дифференциала функции называется ее дифференцированием, при этом вычисляется производная, поэтому процесс вычисления производной часто называется дифференцированием.

Дифференциал – главная линейная часть приращения функции.

Функция, обладающая дифференциалом, называется дифференцируемой.

У дифференцируемой функции производная должна быть конечной.

Свойства дифференциала

1. ;

2. ;

3. .

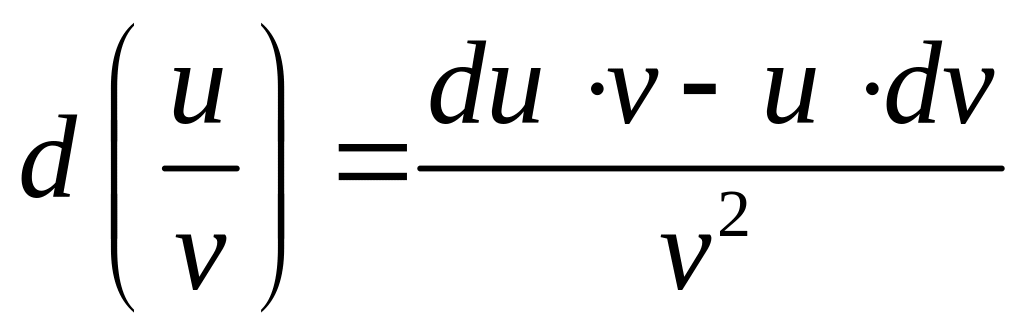Найдем выражение для дифференциала сложной функции: , где . По правилу дифференцирования сложной функции: , то есть - инвариантность дифференциала – дифференциал сложной функции имеет такой же вид, как и для простой переменной.

Дифференциал широко применяется в приближенных вычислениях.

Дифференциал , если .

7.10. Производные и дифференциалы высших порядков

Если вычислить производную от первой производной у’, то получим вторую производную: . Производная от второй производной: – третья производная. Производная n-го порядка – производная от производной (n –1) порядка: .

Пример: ;

.

Для дифференцируемых функций u и v:

;

- формула Лейбница.

Дифференциалы высших порядков.

Дифференциал второго порядка:

, ;

- дифференциал n-го порядка.

Глава 8. Основные теоремы дифференциального исчисления

8.1. Теорема Ферма

Пусть f(x) определена на интервале и в точке интервала достигает наибольшего (наименьшего) значения. Тогда, если в x_o существует производная, то она равна 0, т.е. f′ (x_o) =0.

Пусть в точке x_o f(x) принимает наибольшее значение, значит , f(x_o) ≥ f(x) для любого

x . Для любой точки (x_o +∆x) ∆у = f(x_o +∆x) – f(x₀) ≤ 0.

Если ∆x>0 (x>x_o), то ∆у/ ∆х ≤ 0 и = ≤ 0. Если ∆x <0 (x < хo), то ∆у/∆x ≥ 0 и . По условию существует, значит .