6.4. Бесконечно большие величины

Функция ƒ(x) → при , то есть является бесконечно большой величиной при , если для каждого M > 0, как бы велико оно не было, можно найти такое δ > 0, что для всех , удовлетворяющих неравенству имеет место |ƒ(x)|>M. Запись: .

Свойства:

1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.

Замечание 1. Если и – бесконечно большие величины при , то – неопределенность . – неопределенность .

Теорема. Если – бесконечно малая при , то величина – бесконечно большая при и наоборот.

6.5. Основные теоремы о пределах

1. Предел алгебраической суммы конечного числа переменных равен алгебраической сумме пределов этих переменных.

.

2. Предел произведения конечного числа переменных равен произведению пределов этих переменных.

.

Следствие.

Постоянный множитель можно выносить за знак предела.

3. Предел частного двух переменных равен частному пределов этих переменных, если предел делителя отличен от нуля, 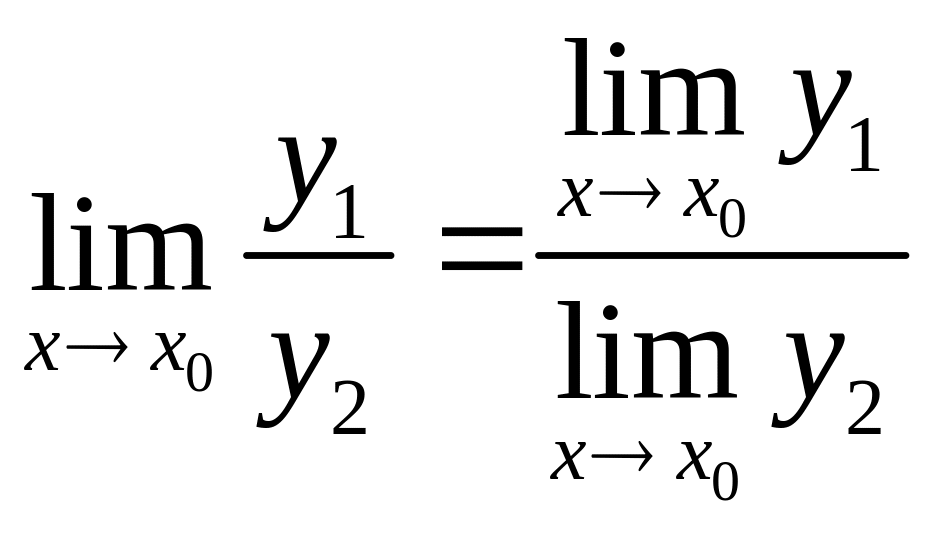, если .

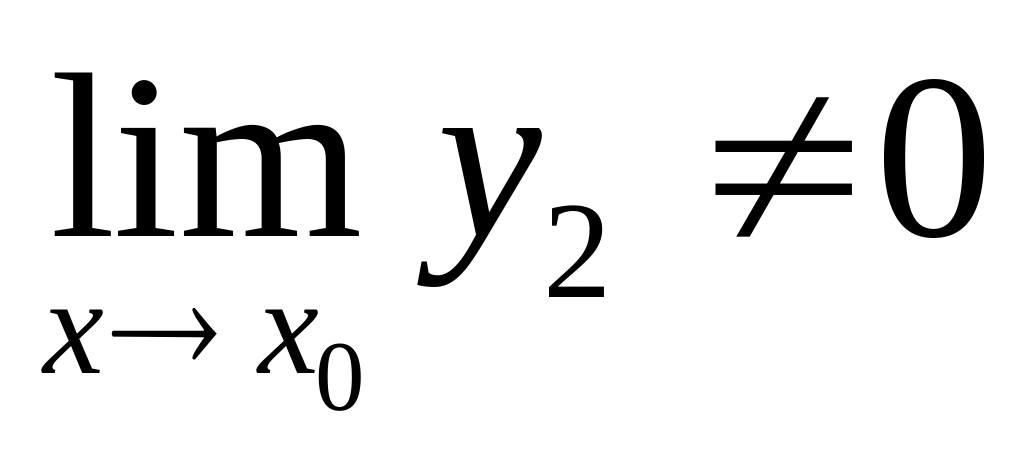4. Если , , то предел сложной функции .

5. Если в некоторой окрестности точки (или при достаточно больших ) , то .

6. Если в некоторой окрестности точки (или при достаточно больших ) функция заключена между двумя функциями и , имеющими одинаковый предел А при ,то функция имеет тот же предел.

Во всех этих теоремах предполагается существование пределов этих функций.

6.6. Признаки существования предела

Теорема. Функция не может иметь более одного предела.

Доказательство. Предположим противное, т.е. функция имеет два предела А и B, ; и .

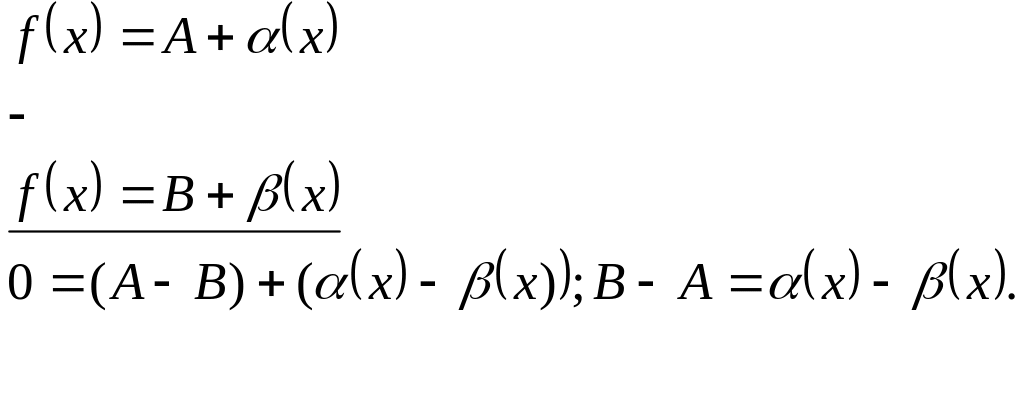
В левой части равенства – число, отличное от 0, в правой – бесконечно малая величина, чего быть не может. Наше предположение о наличии двух пределов неправильно.

Теорема. Если числовая последовательность монотонна и ограничена, то она имеет предел.

6.7. Первый замечательный предел

Первый замечательный предел: .

Доказательство. Возьмем окружность радиуса R, пусть .

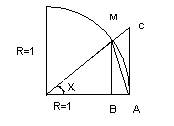Из рисунка: S_∆МОА< S_{сектора МОА} <S_∆CОА. ; , , делим на , 1 < < или 1> >cosx . cosx = 1. = , поэтому

1

6.8. Второй замечательный предел

Рассмотрим последовательность и докажем, что она сходится. Для этого достаточно показать, что она возрастающая и ограниченная сверху. Для представления х_n применим формулу биноме Ньютона:

или: ;

.

при 0 < k < n, то есть каждое слагаемое в x_n+1 > x_n и у x_n+1 добавляется еще одно положительное слагаемое, поэтому x_n < x_n+1 , т.е. последовательность возрастающая. Каждое выражение в скобках <1 и (при n>2), . Используя сумму геометрической прогрессии, имеем: 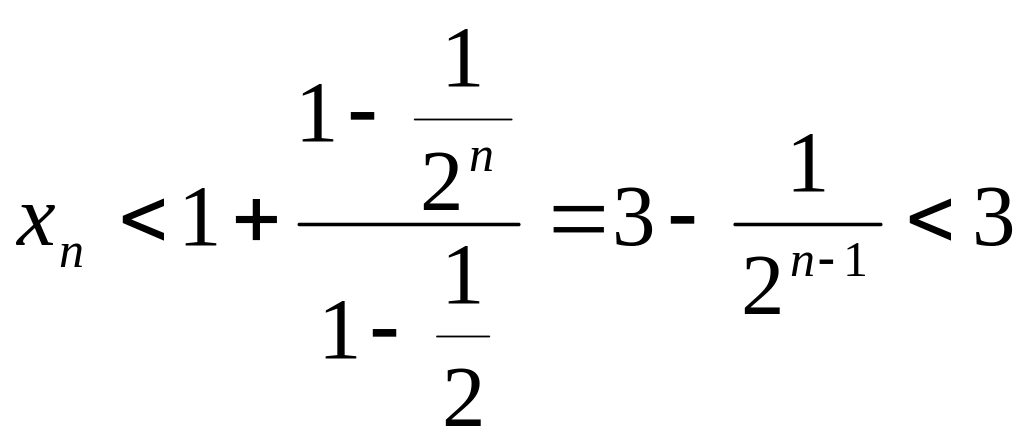. Последовательность монотонно возрастает и ограничена сверху, поэтому она имеет предел. Этот предел называют числом , е=2,7182818284…, 2<е<3. В общем виде: , или .