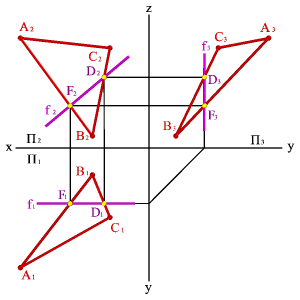
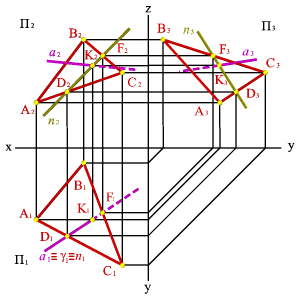
3. Скрещивающиеся прямые

Скрещивающимися называются две непараллельные прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

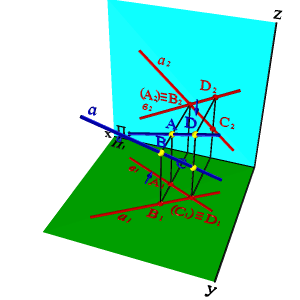
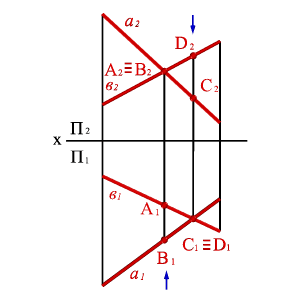
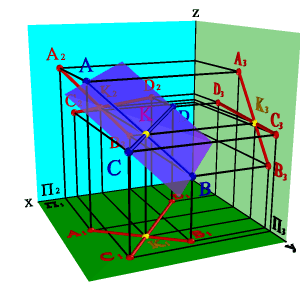
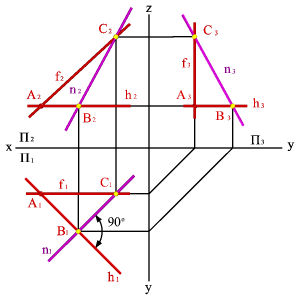
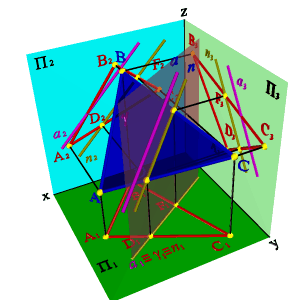
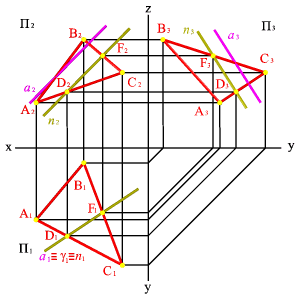
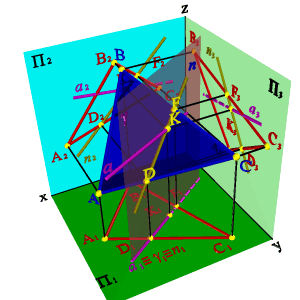
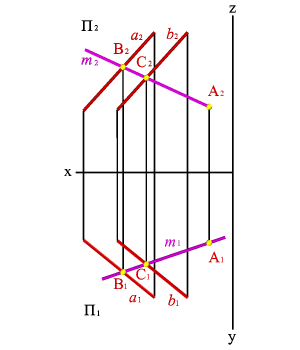
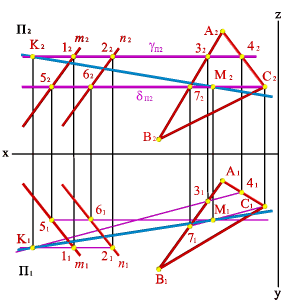
Точке пересечения фронтальных проекций прямых (рис. 38) соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю.

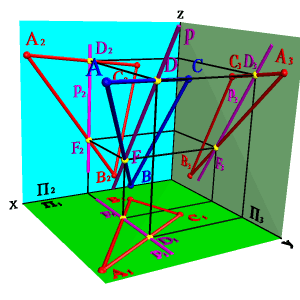
а) модель		б) эпюр
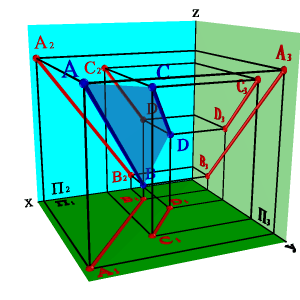
Рисунок 38. Скрещивающиеся прямые

На предложенном примере ближе точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и  фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично).

Этот способ определения видимости по конкурирующим точкам. В данном случае  точки А и В- фронтально конкурирующие, а С и D -горизонтально конкурирующие.

Проекции плоских углов

Угол - геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.

Углом между прямыми называется меньший из двух смежных углов, лучи которых параллельны этим прямым.

Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость.

Рассмотрим ряд свойств ортогональных проекций плоских углов:

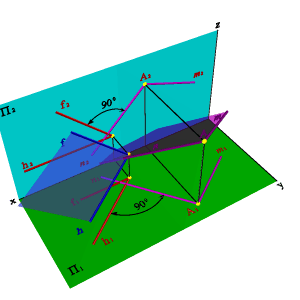
1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла).

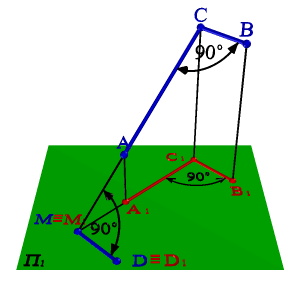
Дано:  АСВ = 90^о; [ВС] // П₁; [АС]  П₁.

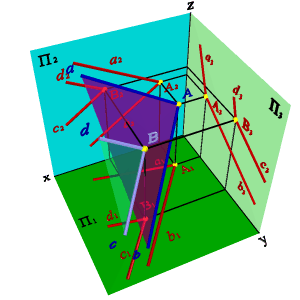
Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П₁ (рис. 39) получим горизонтальный след прямой -  точку М  М₁, одновременно принадлежащую прямой и ее проекции. Из условия следует, что [ВС] // [В₁С₁]. Если через точку М проведем прямую  МD параллельную С₁В₁ , то она будет параллельна и СВ и перпендикулярна СМ, а следовательно   СМD= 90^о. Согласно обратной теореме о трех перпендикулярах (Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.)  С₁МD=90^о. Таким образом, [MD][А₁С₁] и [MD]//[В₁С₁], следовательно,  А₁С₁В₁= 90^о, что и требовалось доказать.  В случае, когда [АС]П₁ проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.

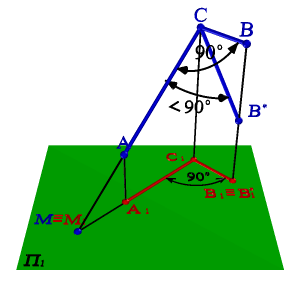
Рисунок 39. Теорема о проецировании прямого угла		Рисунок 40. Обратная теорема о проецировании прямого угла

2. Если проекция угла представляет угол 90⁰, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций (рис. 40).

3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу. 

4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.

5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.

Плоскость

Плоскость* – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:

1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:

Ax+By+Cz+D=0,

где А, В, С, и D - постоянные, причем А, В и С одновременно не равны нулю.

• Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил

Способы задания плоскостей

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

1. тремя точками, не лежащими на одной прямой линии (рис.41);

а) модель		б) эпюр
Рисунок 41. Плоскость, заданная тремя точками, не лежащими на одной прямой

2. прямой линией и точкой, не принадлежащей этой прямой (рис.42);

а) модель		б) эпюр
Рисунок 42. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии

3. двумя пересекающимися прямыми (рис.43);

а) модель		б) эпюр
Рисунок 43. Плоскость, заданная двумя пересекающимися прямыми

4. двумя параллельными прямыми (рис.44);

а) модель		б) эпюр
Рисунок 44. Плоскость, заданная двумя параллельными прямыми

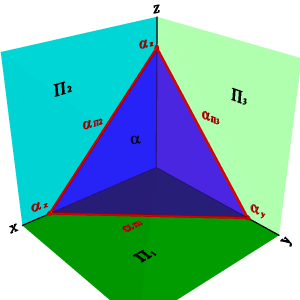
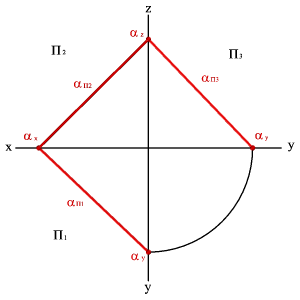
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).

Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная  плоскость различают горизонтальный_П1, фронтальный _П2 и профильный _П3 следы.

а) модель		б) эпюр
Рисунок 45. Плоскость, заданная следами

Следы плоскости общего положения пересекаются  попарно на осях в точках _x,_y,_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

положение плоскости относительно плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный _П1; - фронтальный _П2; - профильный _П3).

2. Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (П_), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек  этой плоскости  совпадают с горизонтальным следом (рис.46).

а) модель		б) эпюр
Рисунок 46. Горизонтально проецирующая плоскость
а) модель		б) эпюр
Рисунок 47. Фронтально проецирующая плоскость
а) модель		б) эпюр
Рисунок 48. Биссекторная плоскость

2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (П₂)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости  является прямая линия, совпадающая со следом  _П2 (рис.47).

2.3. Плоскость, перпендикулярная профильной плоскости ( П₃) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.48).

3. Плоскости, параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельна исследуемая плоскость, различают:

3.1. Горизонтальная  плоскость - плоскость, параллельная горизонтальной плоскости проекций (П₁) -  (П₂,П₃). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П₁ без искажения, а на плоскости П₂ и П₃ в прямые - следы плоскости  _П2 и _П3 (рис.49).

а) модель		б) эпюр
Рисунок 49. Горизонтальная плоскость

2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (П₂), (П₁, П₃).

а) модель		б) эпюр
Рисунок 50. Фронтальная плоскость

Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П₂ без искажения, а на плоскости П₁ и П₃ в прямые - следы плоскости  _П1 и _П3 (рис.50).

2. Профильная плоскость - плоскость, параллельная профильной плоскости проекций (//П₃), (П₁, П₂). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П₃ без искажения, а на плоскости П₁ и П₂ в прямые - следы плоскости  _П1 и _П2 (рис.51).

а) модель		б) эпюр
Рисунок 51. Профильная плоскость
Следы плоскости

Следом плоскости называется линия пересечения плоскости с плоскостью проекций. В зависимости, от того с какой из плоскостей проекций пересекается данная плоскость, различают: горизонтальный, фронтальный и профильный следы плоскости.

^{Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой (как для построения любой прямой).}

а) модель		б) эпюр
Рисунок 52. Построение следов плоскости

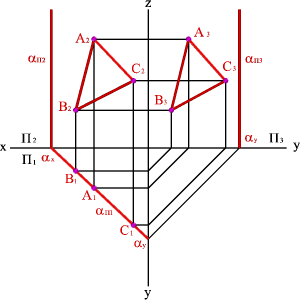
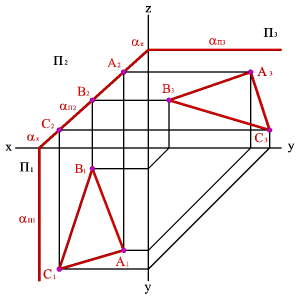
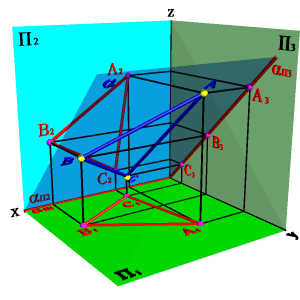
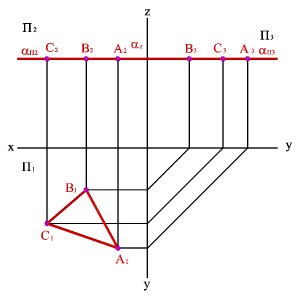
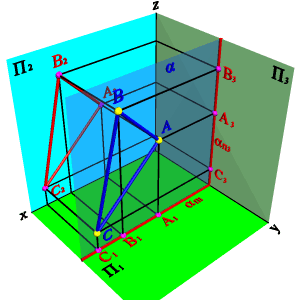
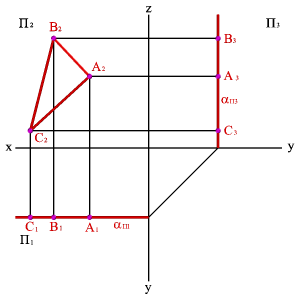
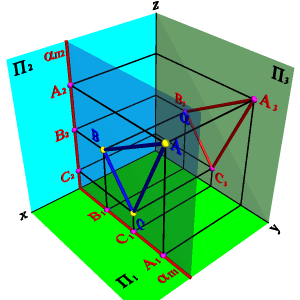
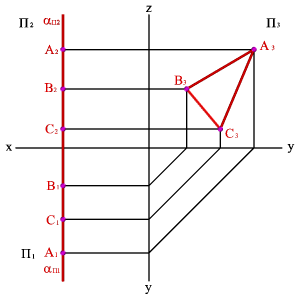
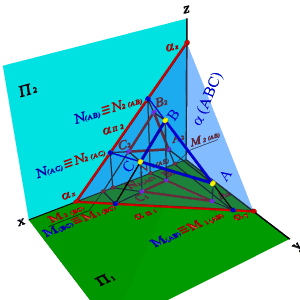
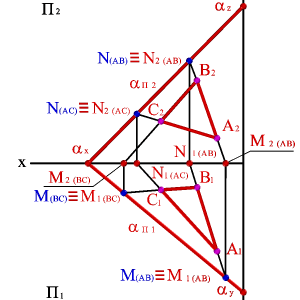
^{На рисунке 52 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости α}_П2 ^{построен, как прямая соединяющая две точки N}_(АС) ^{и N}_(АВ)^{, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный след α}_П1 ^{– прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след α}_П3 ^{– прямая соединяющая точки (α}_y ^{и α}_z^{) пересечения горизонтального и фронтального следов с осями. Точки α}_x^{, α}_y ^{и α}_z ^{называют точками схода следов.}

Взаимное расположение прямой и плоскости

Известны три варианта взаимного расположения прямой и плоскости:

1. Прямая принадлежит плоскости.

2. Прямая параллельна плоскости.

3. Прямая пересекает плоскость.

Прямые линии, принадлежащие плоскости и занимающие частное положение по отношению к плоскостям проекций, называются главными линиями плоскости.

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

Определение взаимного положения прямой и плоскости - позиционная задача, для  решения которой применяется метод вспомогательных секущих плоскостей.

Сформулируем условие принадлежности прямой плоскости как аксиомы:

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Проиллюстрируем примерами использование этих аксиом.

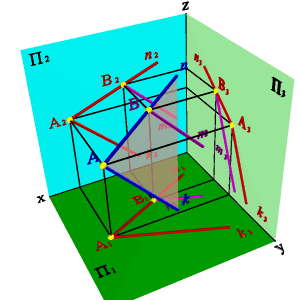
Задача. Дана плоскость (n,k) и одна проекция прямой m₂ (рис.53).

 

а) модель		б) эпюр
Рисунок 53. Прямая и плоскость имеют две общие точки

Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.

Проекция прямой m₂ пересекает проекции прямых n₂ и k₂ в точках В₂ и С₂ соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.

Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.

Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис.54).

Пусть точка В принадлежит прямой n, лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию  В₂ проведем проекцию прямой m₂ параллельно прямой k₂, для нахождения недостающих проекций прямой необходимо построить проекцию точки В₁,  как точки лежащей на проекции прямой n₁ и через неё провести проекцию прямой m₁  параллельно проекции k₁.

Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме 2 прямая принадлежит этой плоскости.

а) модель		б) эпюр
Рисунок 54. Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

Главные линии плоскости

Среди прямых линий, принадлежащих плоскости, особое значение имеют прямые, занимающие частное положение в пространстве:

1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎ ABC, h//P₁, h₂//Ох,h₃// Оy)(рис.55). 

а) модель		б) эпюр
Рисунок 55. Горизонталь

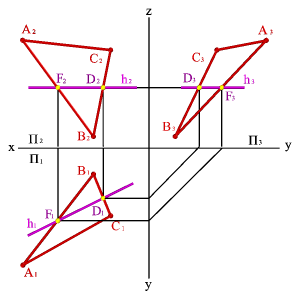
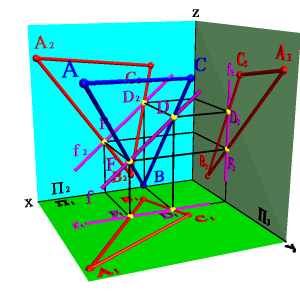
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎ ABC, f//P₂, f₁// Ох, f₃// Оz)(рис.56).

а) модель		б) эпюр
Рисунок 56. Фронталь

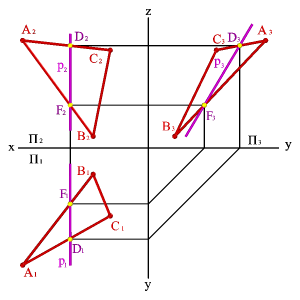
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рÎ ABC , р//P₃, р₁^ Ох, р₂^ Ох) (рис.57).

а) модель		б) эпюр
Рисунок 57. Профильная прямая

Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

4. Прямые, принадлежащие плоскости и образующие с плоскостью проекций наибольший угол называются линиями наибольшего наклона данной плоскости к плоскости проекций. С помощью линий наибольшего наклона определяют двугранные углы между заданной плоскостью и соответствующей плоскостью проекций.

Прямые плоскости, перпендикулярные соответствующим линиям уровня являются линиями наибольшего наклона.

Линия наибольшего наклона к горизонтальной плоскости проекций называется линией ската. Такое название объясняется тем, что эта линия является траекторией, по которой шарик скатывается с данной плоскости. По отношению к плоскостям П₂ и П₃ целесообразнее употреблять название линия наибольшего наклона.

Линия ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.58). Горизонтальная проекция линии ската плоскости общего положения перпендикулярна горизонтальной проекции горизонталь этой плоскости. Фронтальная и профильная проекции ската строятся по её принадлежности плоскости.

а) модель		б) эпюр
Рисунок 58. Линия наибольшего ската

Прямая, параллельная плоскости
а) модель		б) эпюр
Рисунок 59. Прямая параллельная плоскости

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости.

Задача. Дано: плоскость общего положения ABC и прямая общего положения а.

Требуется оценить их взаимное положение (рис.59). 

Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей g и АВС - прямую п (DF). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а₁ и со следом плоскости g. Проекция прямой п₂ параллельна а₂, п₃ параллельна а₃, следовательно, прямая а параллельна плоскости AВС.

Прямая пересекает плоскость

Нахождение точки пересечения прямой линии и плоскости – одна из основных задач начертательной геометрии.

Задача. Дано: плоскость AВС и прямая а.

Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.

Алгоритм решения задачи (рис.60):

1. Через горизонтальную проекцию прямой а₁ проведем вспомогательную горизонтально проецирующую плоскость g (таким образом а Î g).

а) модель		б) эпюр
Рисунок 60. Нахождение точки пересечения прямой и плоскости

2. Находим линию пересечения вспомогательной плоскости с заданной. Горизонтальный след плоскости g₁ пересекает проекцию плоскости A₁В₁С₁ в точках D₁ и F₁, которые определяют положение горизонтальной проекции п₁- линии пересечения плоскостей g и AВС. Для нахождения фронтальной  и профильной проекции п спроецируем точки D и F на фронтальную  и профильную плоскости проекций.

3. Определяем точку пересечения прямых а и п. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает  проекции а в точке К, которая и является  проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К₁.

4. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.

Прямая, перпендикулярная плоскости

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

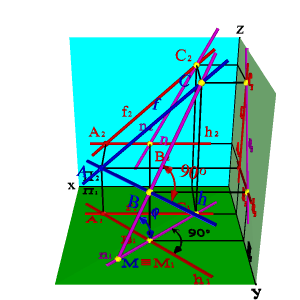
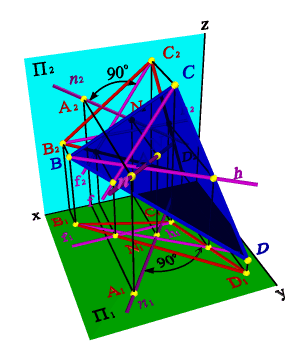
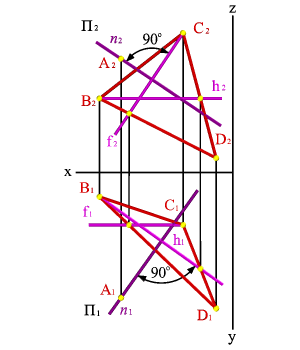
Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n₁h₁. Аналогично для фронтали – fn   f₂ n₂.

Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.

Доказательство следует из теоремы о проецировании прямого угла.

Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.61).

Задача. Дано: плоскость ВСD и точка А.

Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.

В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А₁ прямую n₁ перпендикулярно горизонтальной проекции горизонтали h₁, а на фронтальной плоскости проекций через точку А₂ прямую n₂ перпендикулярно фронтальной проекции фронтали f₂, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.

а) модель		б) эпюр
Рисунок 61. Прямая, перпендикулярная плоскости

Взаимное расположение точки и плоскости

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.

Если точка принадлежит плоскости, то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.

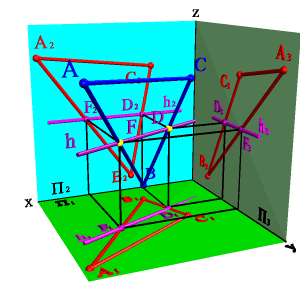
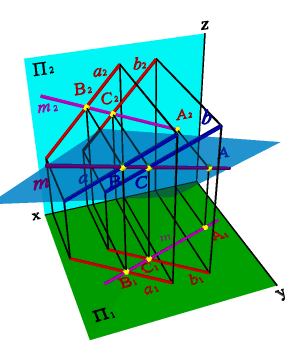
Рассмотрим пример (рис.62). Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).

Задача. Дано: плоскость a(а,b) и  фронтальная проекция точки А.

Требуется построить горизонтальную проекцию точки А, если известно, что она лежит в плоскости a(а,b).

а) модель		б) эпюр
Рисунок 62. Точка, принадлежащая плоскости

Через точку А₂ проведем проекцию прямой m₂, пересекающую проекции прямых a₂ и b₂  в точках С₂ и В₂ (СÎ a,BÎ aÞ mÎ a). Построив проекции точек С₁ и В₁, определяющие положение m₁, находим горизонтальную проекцию точки А (А₁Î m₁, mÎ aÞ АÎ a).

Взаимное расположение плоскостей

Две плоскости в пространстве могут быть либо параллельны (в частном случае совпадать друг с другом), либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

Параллельные плоскости

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. 

Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми (a,b)  (рис.63).

Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми (a,b) и точка В.

Требуется через точку В провести плоскость, параллельную плоскости (a,b)  и задать её двумя пересекающимися прямыми c и d.

Согласно определения, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны между собой.

Для того, чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой.

d//a, с//b  Þ d₁//a₁, с₁//b₁; d₂//a₂ , с₂//b₂; d₃//a₃, с₃//b₃.

а) модель		б) эпюр
Рисунок 63. Параллельные плоскости

пересекающиеся плоскости

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.64).

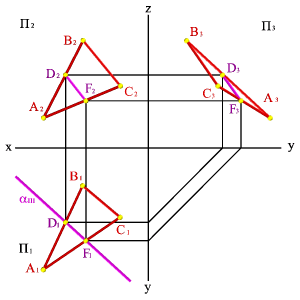
Задача. Дано: плоскость общего положения, заданная треугольником АВС, а вторая плоскость - горизонтально проецирующая a.

Требуется построить линию пересечения заданных плоскостей.

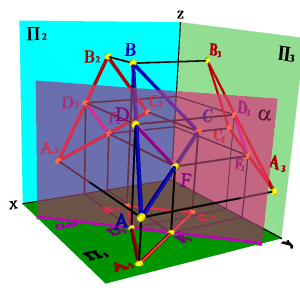
Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью a - точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как a - горизонтально проецирующая плоскость, то проекция D₁F₁ совпадает со следом плоскости a_П1, таким образом остается только построить недостающие проекции [DF] на П₂ и П₃.

а) модель		б) эпюр
Рисунок 64. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью

Рассмотрим общий случай пересечения плоскостей, когда плоскости занимают общее положение в пространстве.

Задача. Дано: Две плоскости общего положения a(m,n) и b (ABC) (рис.65).

Требуется построить линию пересечения плоскостей a и b .

а) модель		б) эпюр
Рисунок 65. Пересечение плоскостей общего положения

Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с заданными плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точка пересечения этих прямых - К, которая одновременно принадлежит трем плоскостям a, b и g, т.е. искомой линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C), точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом, прямая (КМ) является линией пересечения плоскостей a и b .

Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость. В этом случае точки, определяющие положение линии пересечения плоскостей, находятся как точки пересечения прямой и плоскости.

взаимно перпендикулярные плоскости

Частный случаем пересечения плоскостей являются взаимно перпендикулярные плоскости.

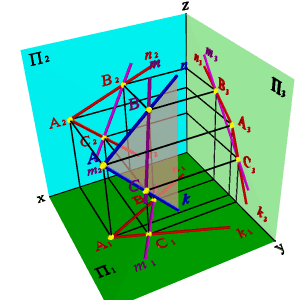
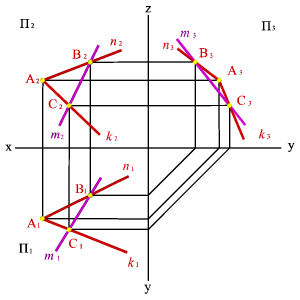
Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей, перпендикулярных данной плоскости a(h,f). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a. Для того, чтобы через точку А провести плоскость, перпендикулярную плоскости a(h,f), необходимо из точки А провести прямую n, перпендикулярную плоскости a(h,f), (горизонтальная проекция n₁ перпендикулярна горизонтальной проекции горизонтали h₁, фронтальная проекция n₂ перпендикулярна фронтальной проекции фронтали f₂). Любая плоскость, проходящая через прямую n будет перпендикулярна плоскости a(h,f), поэтому для задания плоскости через точку А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми (m,n), будет перпендикулярна плоскости a(h,f)(рис.66).

а) модель		б) эпюр
Рисунок 66. Взаимно перпендикулярные плоскости

 

Многогранники

Многогранник* в трехмерном пространстве - совокупность конечного числа  плоских многоугольников такая, что

1) которых каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);

2) от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого в свою очередь - к смежному с ним, и т.д.

Эти многоугольники называются гранями, их стороны ребрами, а их вершины - вершинами многогранника.

Многогранник**, полиэдр, - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками - гранями. Стороны граней называются ребрами, а концы ребер - вершинами. По числу граней различают 4-гранники, 5-гранники и т.д. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой его грани. Многогранник называется правильным, если его грани правильные многоугольники (т.е. такие, у которых все стороны и углы равны) и все многогранные углы при вершинах равны. Существует пять видов правильных многогранников: тетраэдр, куб (гексаэдр), октаэдр, додекаэдр, икосаэдр.

Виды Многогранников

Кратко охарактеризуем геометрические свойства некоторых многогранников:

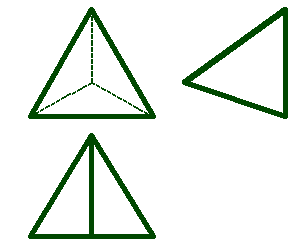
1. Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.67).

а) модель		б) эпюр
Рисунок 67. Пирамида

3. Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
Рисунок 68.  Призма

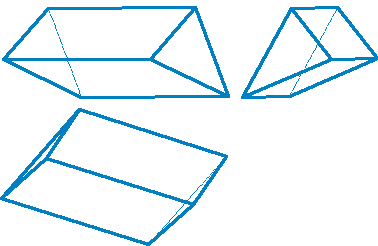
3. Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

4.   Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Тетраэдр - правильный четырехгранник (рис.70). Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).

а) модель		б) эпюр
Рисунок 70. Тетраэдр

Гексаэдр - правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

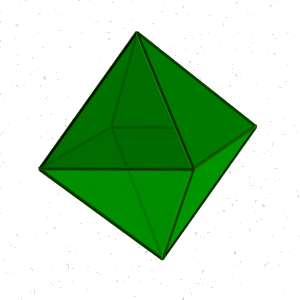
Октаэдр - правильный восьмигранник (рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

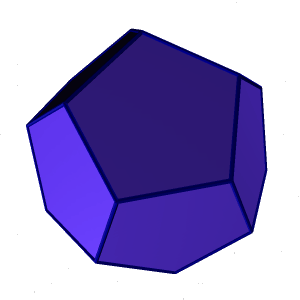
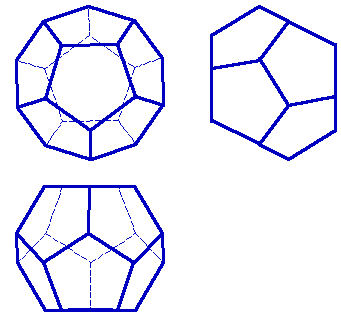
Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73).

а) модель		б) эпюр
Рисунок 73. Додекаэдр

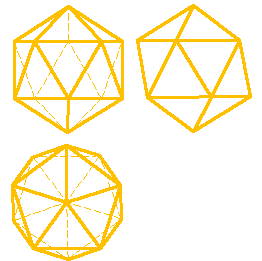
Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74).

а) модель		б) эпюр
Рисунок 74. Икосаэдр

5.   Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру (рис. 75). Это малые тетраэдры, основания которых совпадают с гранями октаэдра. Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.

Рисунок 75. Звездчатый октаэдр		Рисунок 76. Малый звездчатый додекаэдр

Малый звездчатый додекаэдр - (рис.76) звездчатый додекаэдр первого продолжения. Он образован продолжением граней выпуклого додекаэдра до их первого пересечения. Каждая грань выпуклого додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые "куски", внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра. При дальнейшем продолжении граней до нового пересечения образуется средний звездчатый додекаэдр - звездчатый додекаэдр второго продолжения. Последней же звездчатой формой правильного додекаэдра является звездчатый додекаэдр третьего продолжения - большой звездчатый додекаэдр. Он образован продолжением граней звездчатого додекаэдра второго продолжения до их нового пересечения.

пересечение плоскости с многогранником

Построение сечения многогранника требует многократного решения задачи о нахождении точки пересечении прямой с плоскостью. Точки, в которых ребра многогранника пересекаются с заданной плоскостью, будут вершинами искомого сечения.

Тот же результат можно получить, сведя задачу к построению линий пересечения плоскости с гранями тела.

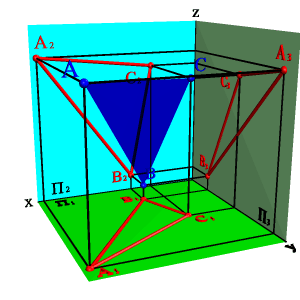
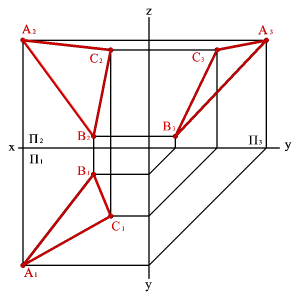
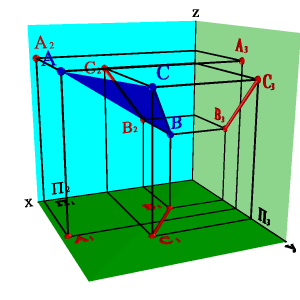
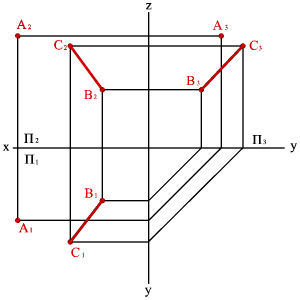
Задача. Дана призма и плоскость общего положения заданная двумя пересекающимися прямыми а и b (рис.77). Необходимо построить сечение призмы данной плоскостью.

а) модель
б) эпюр
Рисунок 77. Пересечение плоскости общего положения с призмой

Решим поставленную задачу нахождением точек пересечения ребер призмы с плоскостью. Для чего, через горизонтальные проекции ребер проведем вспомогательные секущие плоскости α, β и γ. Построив линии пересечения вспомогательных плоскостей с заданной, находим на фронтальной проекции точки пересечения их с соответствующими ребрами призмы К₂, М₂ и N₂ – вершины фронтальной проекции сечения призмы. По линиям связи находим горизонтальные проекции этих точек. Полученные точки соединяем прямыми линиями, с учетом видимости. При решении вопроса о видимости сторон построенного сечения следует иметь в виду достаточно очевидное правило: точка и линия, лежащие на поверхности многогранника, видимы только в том случае, если они расположены на видимой грани.

пересечение Прямой линии с многогранником

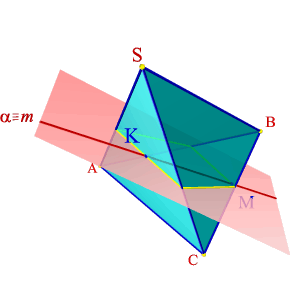
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с плоскостями граней (рис.78).

Алгоритм решения задачи:

1. Через заданную прямую m проводим вспомогательную секущую плоскость a (mÎ a).

2. Строим сечение многогранника со вспомогательной секущей плоскостью a.

3. Определить искомые точки К,М – пересечения полученного сечения с прямой m.

4. Определить видимость прямой по отношению к пирамиде.

а) модель		б) эпюр
Рисунок 78. Пересечение прямой линии с пирамидой

взаимное пересечение многогранников

Построение линии взаимного пересечения многогранных поверхностей можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:

1.Определяют точки, в которых ребра одной из многогранных поверхностей пересекают грани другой и ребра второй пересекают грани первой (задача на пересечение прямой с плоскостью). Через найденные точки в определенной последовательности проводят ломаную линию, представляющую собой линию пересечения данных многогранников. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.

2. Определяют отрезки прямых, по которым грани одной поверхности пересекают грани другой (задача на пересечение двух плоскостей между собой); эти отрезки являются звеньями ломаной линии, получаемой при пересечении многогранных поверхностей.

Если проекция ребра одной из поверхностей не пересекает проекции грани другой, хотя бы на одной из проекций, то данное ребро не пересекает этой грани. Однако пересечение проекций ребра и грани еще не означает, что ребро и грань пересекаются в пространстве.

а) модель		б) эпюр
Рисунок 79. Пересечение пирамиды с призмой

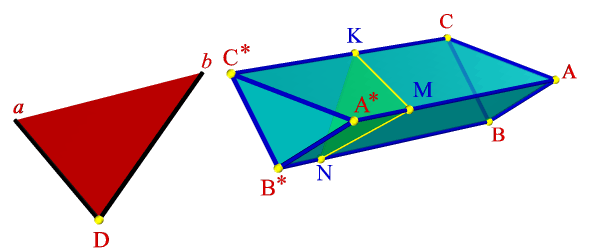
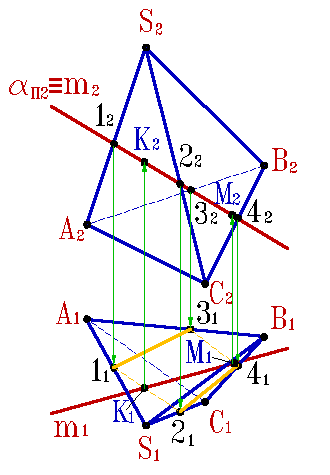
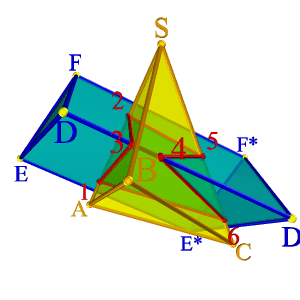
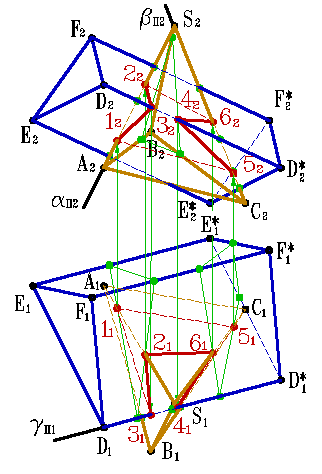
На примере (рис.79) показано пересечение поверхности треугольной призмы с треугольной пирамидой. Построение основано на нахождении точек пересечения ребер одного многогранника с гранями другого. На рисунке 79 б показано построение линии пересечения пирамиды АВСS и треугольной призмы DEFD*E*F*. 

Для нахождения точек 1 и 2 в которых ребро пирамиды AS пересекает грани DD*EE* и DD*FF* призмы, через проекцию ребра A₂S₂ проведена фронтально проецирующая плоскость _П2, которая пересекает ребра призмы в  трех точках, горизонтальные проекции  этих точек пересечения плоскости  с ребрами призмы, образуют треугольник. Проекция ребра пирамиды A₁S₁ пересекает полученный треугольник в точках 1₁ и 2₁.

С помощью фронтально проецирующей плоскости β, находим точки 5 и 6 пересечения ребра пирамиды SC с гранями призмы DD*FF* и DD*EE*, а при помощи горизонтально проецирующей плоскости  находим точки 3 и 4 пересечения ребра призмы с гранями пирамиды. Соединив полученные точки, с учетом видимости, получим пространственную ломаную линию – линию пересечения данных многогранников.

Кривые линии

Кривая линия - это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному.

 В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством и т.д.

Например, (рис.80) циклоида – траектория движения точки окружности, катящейся без скольжения по прямой линии. Эта кривая состоит их ряда «арок», каждая из которых соответствует полному обороту окружности.

Рисунок 80. Циклоида

Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую.

Различны и способы задания кривых:

· аналитический – кривая задана математическим уравнением;

· графический – кривая задана визуально на носителе графической информации;

· табличный – кривая задана координатами последовательного ряда точек.

Уравнением кривой линии называется такое соотношение между переменными, которому удовлетворяют координаты точки, принадлежащей кривой.

В основу классификации кривых положена природа их уравнений.

Кривые подразделяются на алгебраические и трансцендентные в зависимости от того, являются ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.

Плоская кривая линия называется алгебраической, если её уравнение f (xy)=0, причём функция f (xy) является степенным множителем относительно переменных х и у; в остальных случаях кривая называется трансцендентной.

Кривая линия, представленная в декартовых координатах уравнением п-й степени, называется алгебраической кривой п-го порядка.

Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные пространственными.

Плоские Кривые линии

Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими.

Порядок плоской алгебраической кривой линии определяется наибольшим числом точек её пересечения прямой линией. Любая прямая линия может пересекать алгебраическую кривую линию п-го порядка не более, чем в п точках. 

Рассмотрим несколько примеров алгебраической кривой линии:

Рисунок 81. Парабола

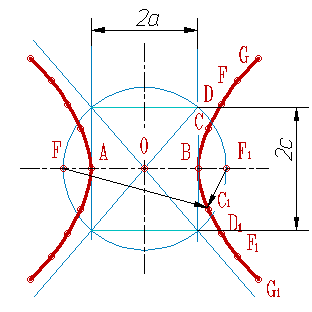
Рисунок 82. Гипербола

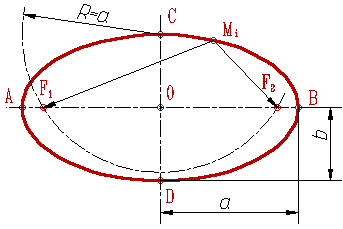
Рисунок 83. Эллипс

1. Парабола – кривая второго порядка, прямая пересекает ее в двух точках (рис.81). При этом парабола может быть определена как:

-множество точек М(A,B,C,...) плоскости, расстояние которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию  до определенной прямой DD₁ - директрисы параболы;

-линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса;

-в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0х направленной по оси параболы уравнение параболы имеет так называемый канонический вид 

y²=2px,

где р (фокальный параметр) - расстояние от фокуса до директрисы.

2. Гипербола :

- множество точек М(A,B,C,...) плоскости, (рис.82) разность (по абсолютной величине) расстояний которых до двух определенных точек F и F₁ этой плоскости (фокусов гиперболы) величина постоянная:

FM - F₁M=2а<2с

Середина 0 отрезка FF₁ (фокусного расстояния) называется центром гиперболы;

- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости;

- в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический вид

х²/а² - у²/b²=1, b²=с² - а²,

где а и b длины полуосей гиперболы.

3. Эллипс :

- множество точек М(xy) плоскости (рис.83), сумма расстояний МF₁ и МF₂ которых до двух определенных точек F₁ и F₂ (фокусов эллипса) постоянна

МF₁+МF₂=2а.

Середина 0 отрезка F₁F₂ (фокусного расстояния) называется центром эллипса;

- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса;

- в прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид:

х²/а²+у²/b²=1, 

где а и b - длины большой и малой полуосей эллипса. При а=b фокусы F₁ и F₂ совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса.

Все, рассмотренные выше, плоские кривые линии можно получить как линии пересечения поверхности прямого кругового конуса с плоскостями, различно расположенными по отношению к оси конуса. Поэтому эти кривые называют кривыми конических сечений.

Трансцендентные кривые в отличие от алгебраических могут иметь бесконечное количество точек пересечения с прямой, точек перегиба, вершин и т.п. 

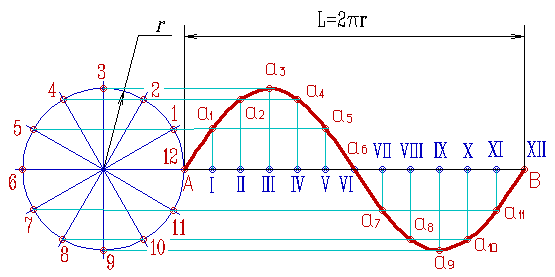
Синусоида - трансцендентная плоская кривая линия (рис.84), получающаяся в результате двойного равномерного движения точки - поступательного и возвратно-поступательного в направлении, перпендикулярном первому.

Рисунок 84. Синусоида

Синусоида - график функции у=sin x, непрерывная кривая линия с периодом Т=2п.

Наряду с этим у трансцендентных кривых могут быть характерные точки, которых не существует у алгебраических кривых: точки прекращения, угловые точки (точки излома), асимптотические точки. Простейшими примерами трансцендентных кривых служат графики функций логарифмической, показательной тригонометрической, а также все спирали, циклоиды и т.п.

Кривая линия как траектория движущейся точки должна быть непрерывной. Движущаяся точка в любом положении должна иметь определенное направление движения. Это направление указывает прямая (касательная), проходящая через рассматриваемую точку.

Длина отрезка кривой линии определяется в общем случае, как сумма длин отрезков, вписанной в нее ломаной линии, с заданной точностью передающей форму кривой.

В практике конструирования линий и поверхностей широко используются обводы. Это кривые, составленные из дуг различных кривых, определенных парами смежных точек. Обводом ряда точек плоскости является плоская кривая, пространства - пространственная. Точки стыка дуг называются узлами. Обвод заданный координатами своих точек называется дискретным. Обвод называется гладким, если дуги обвода в узлах имеют общие касательные.

построение касательной и нормали к плоской кривой

Касательной к кривой линии называется прямая, представляющая предельное положение секущей.

На рисунках 85 и 86 представлены алгоритмы построения касательной к плоской кривой линии соответственно параллельно направлению и из точки, не принадлежащей кривой.

Рисунок 85. Касательная к кривой параллельная заданному направлению		Рисунок 86. Касательная к кривой из заданной точки

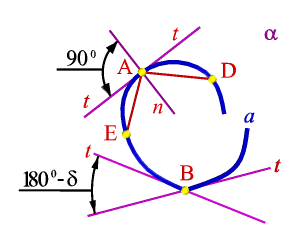
Рисунок 87. Касательная в точке кривой

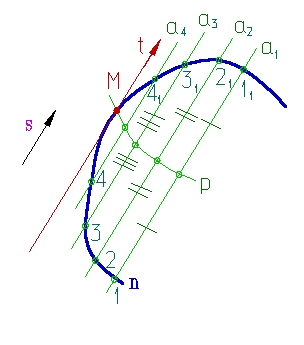
Рисунок 88. Построение нормали к кривой

Для построения касательной в точке плоской кривой как видно из рисунка 87 используется две секущие хорды. Рассмотрим построение касательной в точке А. Для этого проведем секущие хорды АЕ и АD. Если точку Е приближать к точке А, секущая АЕ поворачивается вокруг точки А. Когда точка Е совпадет с точкой А (А≡Е) секущая АЕ достигнет своего предельного положения t. В этом предельном положении секущая называется полукасательной к кривой а в точке А. Секущая АD в предельном положении А≡D также представлена полукасательной t.

Кривая линия в точке А имеет две полукасательные прямые, которые совпадают и определяют одну касательную к кривой линии в точке А – кривая в этой точке называется гладкой (плавной).

Кривая плавная во всех её точках называется гладкой (плавной) кривой линией.

На кривой линии могут быть точки, в которых разнонаправленные полукасательные не принадлежат одной прямой, а составляют между собой угол. Так на кривой а в точке В угол δ между полукасательными не равен 180⁰. Точка В в этом случае называется точкой излома или выходящей точкой.

Нормалью п в точке А кривой линии называется перпендикуляр к касательной (рис.87).

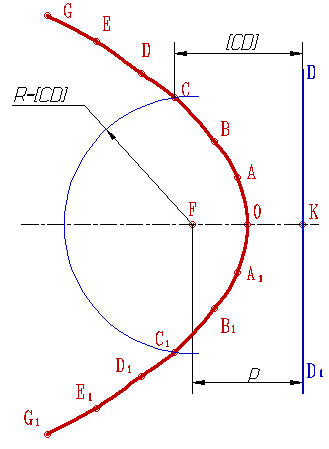
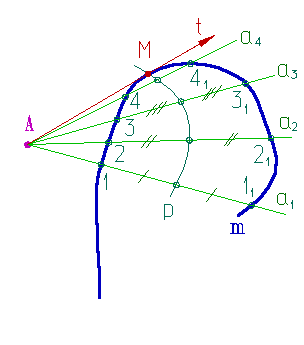
Построение нормали к кривой и проходящей через точку А, не принадлежащую кривой m, можно выполнить следующим образом (рис.88):

1. Проведем окружности а₁, а₂, а₃, а₄, разных радиусов с центром в точке А;

2. Отметим точки пересечения окружностей с кривой -1, 1₁, 2, 2₁, 3, 3₁, 4, 4₁;

3. Из концов хорд восстановим перпендикуляры (при этом перпендикуляры, восстановленные из точек 1, 2, 3, 4, имеют противоположное направление перпендикулярам, восстановленным из точек 1₁, 2₁, 3₁, 4₁);

4. На полученных перпендикулярах отложим отрезки, равные длине соответствующих хорд;

5. Полученные точки соединим плавной кривой l;

6. Пересечение кривых m и l определит положение точки К, через которую пройдет искомая нормаль n.

 

кривизна кривой линии

Рисунок 89. Угол смежности

Плоскую кривую линию можно рассматривать как траекторию движения точки в плоскости (рис.89); точка движется по касательной к кривой линии, обкатывая эту кривую без скольжения.

Движение точки вдоль кривой а связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального положения и угла a поворота касательной относительно начального положения.

Если с увеличением пути S непрерывно увеличивается и a , кривая называется простой.

Угол a (угол смежности) между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяет степень искривленности кривой линии, т.е. определяет кривизну кривой k.

,

предел отношения угла смежности касательных к соответствующей дуге.

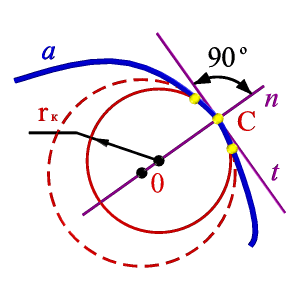
Рисунок 90. Центр и радиус кривизны кривой

Кривизна прямой в любой её точке равна нулю.

Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления.

Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности (рис.90).

Соприкасающейся окружностью или кругом кривизны в данной точке называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки.

Центр соприкасающейся окружности называется центром кривизны кривой в данной точке, а радиус такой окружности – радиусом кривизны кривой линии в данной точке.

Множеством центров кривизны кривой является кривая линия - её называют эволютой данной кривой, а кривая по отношению к своей эволюте называется эвольвентой.

Свойства ортогональных проекций кривой

1. Проекцией кривой линии является кривая линия.

2. Касательная к кривой линии проецируется в касательную к её проекции.

3. Несобственная точка кривой проецируется в несобственную точку её проекции.

4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше.

5. Число узловых точек (в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.

Случаи когда, плоская кривая проецируется в прямую (свойства 1,4,5), а касательная в точку (свойство 2) не учитываются.

Пространственные кривые линии

Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.

Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.