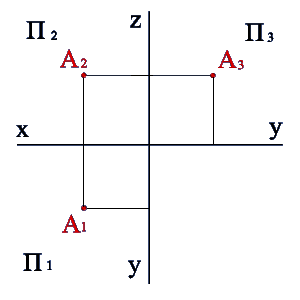
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (a; b).
- •3. Двумя проекциями.
- •2. Для построения фронтального следа n прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.
- •1. Параллельные прямые линии.
- •2. Пересекающиеся прямые.
- •3. Скрещивающиеся прямые
- •Цилиндрическая винтовая линия.
- •Коническая винтовая линия.
- •2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки.
Введение |
Теоретические основы курса "Начертательная геометрия" предназначены для студентов инженерно–технических специальностей (кроме архитектурных и строительных), их содержание соответствуют программе курса начертательной геометрии.
Начертательная геометрия входит в состав учебной дисциплины федерального значения, название которой в зависимости от специальности: «Начертательная геометрия и инженерная графика», «Инженерная и машинная графика» или просто «Инженерная графика». Инженерная графика – это единственная дисциплина целью, которой является непосредственно обучение студентов работе с различной по виду и содержанию графической информацией, основам графического представления информации, методам графического моделирования геометрических объектов, правилам разработки и оформления конструкторской документации, графических моделей явлений и процессов. Графическая информация является средством общения во всех сферах деятельности человека. И в этом смысле в процессе изучения графических дисциплин студент должен приобрести навыки работы с любой по назначению и виду графической информацией от традиционного чертежа и текстового документа до рекламного ролика и Web–страниц, выполненных средствами компьютерной графики.
Государственный образовательный стандарт устанавливает требования к содержанию и объему дисциплины в зависимости от специальности или направления. Содержание начертательной геометрии для специальностей машиностроительного профиля включает следующие темы:
· предмет начертательной геометрии;
· задание точки, прямой, плоскости и многогранников на комплексном чертеже Монжа;
· позиционные задачи;
· метрические задачи;
· способы преобразования чертежа;
· многогранники;
· кривые линии;
· поверхности (поверхности вращения; линейчатые поверхности; винтовые поверхности; циклические поверхности);
· построение разверток поверхностей;
· касательные линии и плоскости к поверхности;
· аксонометрические проекции.
Лекции призваны способствовать самостоятельному изучению начертательной геометрии студентами технических вузов, и являются составной частью авторского учебно-методического обеспечения направленного на реализацию идеи индивидуализации и дифференциации обучения. Использование электронного учебного пособия «Начертательная геометрия», позволяет повысить наглядность и подробность представления учебной информации.
Предмет начертательной геометрии |
В математическом энциклопедическом словаре дается следующее определение: «Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются с помощью их изображений на плоскости».
Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне исследовать предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии.
Изображение фигуры на плоскости как графический способ представления информации о ней имеет преимущества в сравнении с другими способами:
– общение становится более доступным, потому что образы, создаваемые на основе визуального (зрительного) восприятия, обладают большей, чем слова, ассоциативной силой;
– изображения являются интернациональным языком общения, тогда как, например, вербальное общение требует для понимания, как минимум знания языка собеседника.
Таким образом теоретические основы визуализации информации о геометрических объектах, многообразие геометрических объектов пространства, отношения между ними и их графического отображения на плоскости составляют предмет начертательной геометрии.
Задача этой науки – создание оптимальных геометрических форм объектов машиностроения, архитектуры и строительства, разработка теории графического отображения объектов и процессов.
Начертательная геометрия со времен ее основоположника Г. Монжа (1746-1818) завоевала свое достойное место в высшей школе как наука. Важнейшее прикладное значение начертательной геометрии как учебной дисциплины состоит в том, что она учит владеть графическим языком, выполнять и читать чертежи и другие изображения геометрических объектов, без чего немыслимо формирование инженера. Она обеспечивает преемственность между школьными курсами геометрии и черчения и графическими дисциплинами вуза.
Изучение начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления. Совершенствуя нашу способность - по плоскому изображению мысленно создавать представления о форме предмета и наоборот создание изображений мысленно созданных образов – визуализация мысли.
Однако не всякое изображение отображает геометрические свойства оригинала и не может быть принято для всестороннего его исследования. Принципиальное отличие методов изображения, изучаемых в курсе начертательной геометрии, от некоторых современных технических средств отображения (фотография, голография и др.), заключается в возможности с большой наглядностью и метрической достоверностью отобразить не только существующие предметы, но и возникающие в нашем представлении образы проектируемого объекта.
Изображение, которое позволяет определять взаимосвязь (взаимопринадлежность) элементов объекта, называют полным.
Изображения, по которым можно определить размеры объекта, называется метрически определенными.
Из плоскостных изображений объекта наиболее широкое применение в практике получили рисунки и чертежи. Рисунком называют изображение предмета от руки и на глаз с кажущимися относительными размерами и положениями отдельных его элементов. Чертежом называют изображение предмета, построенное по особым правилам с помощью чертежных инструментов в точной зависимости от размеров и положения в пространстве соответствующих линий предмета.
В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне, исследовать предметы и их отдельные детали.
Эти требования к чертежам и привели к созданию теории изображений, составляющей основу начертательной геометрии. Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии
Итак, в курсе начертательной геометрии изучаются:
методы отображения пространственных объектов на плоскости;
способы графического и аналитического решения различных геометрических задач;
приемы увеличения наглядности и визуальной достоверности изображений проецируемого объекта;
способы преобразования и исследования геометрических свойств изображенного объекта;
основы моделирования геометрических объектов.
Виды проецирования. |
Одно из основных геометрических понятий - отображение множеств. В начертательной геометрии каждой точке трехмерного пространства ставится в соответствие определенная точка двумерного пространства – плоскости. Геометрическими элементами отображения служат точки, линии, поверхности пространства. Геометрический объект, рассматриваемый как точечное множество отображается на плоскость по закону проецирования. Результатом такого отображения является изображение объекта.
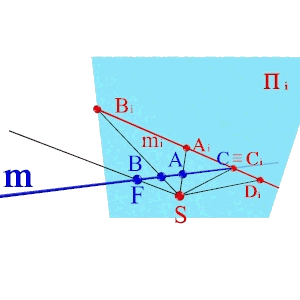
Рисунок 1. Центральное проецирование
В основу любого изображение положена операция проецирования, которая заключается в следующем. В пространстве выбирают произвольную точку S (рис.1) в качестве центра проецирования и плоскость Пi, не проходящая через точку S, в качестве плоскости проекций ( картинной плоскости). Чтобы спроецировать точку А на плоскость Пi , через центр проецирования S проводят луч SА до его пересечения с плоскостью Пi в точке Аi. Точку Аi принято называть центральной проекцией точки А , а луч SА - проецирующим лучом.
Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость.
В евклидовом пространстве существуют точки, которые не имеют центральных проекций, и наоборот в плоскости Пi есть точки, которые в пространстве не имеют оригиналов (точки D и F).
Точка F прямой m принадлежит плоскости , Ω, проходящей через центр проецирования S и расположенной параллельно плоскости проекций, таким образом проецирующий луч SF параллелен плоскости проекций, а точка F, как и все точки лежащие в плоскости Ω не имеют центральных проекций на Пi.
Точка Di проекции прямой mi не имеет оригинала на прямой m, так как проецирующий луч SDi параллелен прямой.
Для исключения подобных случаев евклидово пространство расширяют введением несобственных (бесконечно удаленных) точек. Такое пространство называется расширенным евклидовым пространством.
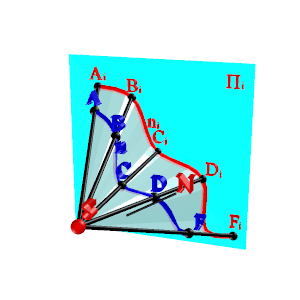
Проецирующие лучи, проведенные через все точки кривой n, образуют проецирующую коническую поверхность N (рис.2). Проекция криволинейной фигуры, таким образом, представляет собой линию пересечения проецирующей поверхности N и плоскости проекций Пi.
|
|
|
|
|
|
Рисунок 2. Центральное проецирование линии Рисунок 3. Центральное проецирование
поверхности
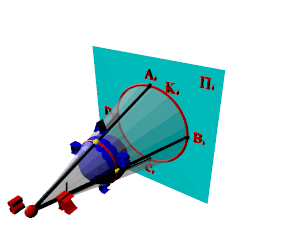
Коническую поверхность К образуют лучи и при проецировании трехмерной фигуры (рис. 3). Линию Ki принято называть в этом случая очерковой или очерком данной фигуры.
Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.
Основными и неизменными его свойствами (инвариантами) являются следующие:
1) проекция точки – точка;
2) проекция прямой – прямая;
3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.
По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых – лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.
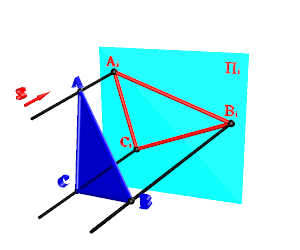
Частный случай центрального проецирования – параллельное проецирование, когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.4). В этом случае полученное изображение называют параллельной проекцией объекта.
При параллельном проецировании сохраняются свойства центрального и добавляются следующие:
проекции параллельных прямых параллельны между собой;
отношение отрезков прямой равно отношению их проекций;
отношение отрезков двух параллельных прямых равно отношению их проекций.
В свою очередь параллельные проекции подразделяются на прямоугольные, когда проецирующие лучи перпендикулярны плоскости проекций, и косоугольные, когда направление проецирования образует с плоскостью проекций угол не равный 900.
Рисунок 4. Параллельное проецирование
Прямоугольное (ортогональное) проецирование является частным случаем параллельного.
Проекция объекта, полученная с использование этого метода, называется ортогональной.
Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.
К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:
1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.
2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.
3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.
4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.
Проекции с числовыми отметками. |
|
|
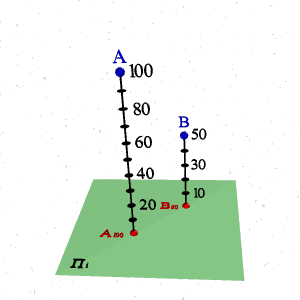
В проекциях с числовыми отметками плоскость проекций Пi называют плоскостью нулевого уровня и обозначают П0. Идея этого метода состоит в том, что на плоскость П0 ортогонально проецируют точку и вместе с проекцией точки задают ее расстояние до плоскости П0 (рис. 5). Это расстояние называют числовой отметкой точки и задают обычно в метрах. Числовую отметку точки пишут внизу справа от обозначения ее изображения. Если плоскость нулевого уровня расположена горизонтально, то чертеж называют планом. На плане всегда указывают линейный масштаб и при необходимости дают ориентацию относительно сторон света. Очень удобно в проекциях с числовыми отметками изображать линии уровня, все точки которых имеют одинаковые отметки. Линии уровня проецируются на П0 без искажения своей формы (применяется в картографии). |
|
||
|
||
Рисунок 5. Метол с числовыми отметками |
||
Проекции с числовыми отметками позволяют просто решать многие задачи. Обратимость чертежей в проекциях с числовыми отметками очевидна.
Зарождение идеи этого метода относят к средним векам. Уже тогда многие народы, пользующие картами с показаниями морских глубин, умели изображать точку при помощи ее проекции и отметки. Однако теоретическое обоснование метод получил лишь в 19 веке, благодаря французскому военному инженеру – капитану Нуазе (1823 г.).
Чертежи в проекциях с числовыми отметками построены на одной плоскости проекций – на одной картине и часто называются однокартинными.
метод монжа |
Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала 19 веков, 1789-1818 гг. одним из основателей знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов.
Постепенно накопившиеся отдельные правила и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometrie descriptive".
Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.
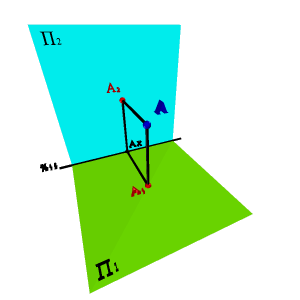
В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. П1 - горизонтальная плоскость проекций, П2- фронтальная. Плоскости бесконечны и непрозрачны.
Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.
|
|
Линия пересечения плоскостей проекций называется осью координат и обозначается x21. Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти. Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис.6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа (франц. Epure – чертеж.) или комплексным чертежом. Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы). Рассмотрим способы их образования, графического задания и возможные варианты положения по отношению к плоскостям проекций. |
|
Рисунок 6. Пространственная модель двух плоскостей проекций |
|||
Точка |
Геометрический объект любой сложности можно рассматривать как геометрическое место точек, по взаимному расположению, которых можно составить представление об объекте, а по расположению их относительно системы координат можно судить о положении его в пространстве.
Точка *- одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.
В современной математике точкой называют элементы весьма различной природы, из которых состоят различные пространства (например, в n-мерном евклидовом пространстве точкой называют упорядоченную совокупность из n- чисел).
Во многих областях математики встречаются точки, имеющие специальные названия. Так, в геометрии изучаются особые точки кривых; в математическом анализе - особые точки решений дифференциальных уравнений, особые точки аналитических функций; в теории множеств - точки, характеризующие свойства рассматриваемого множества (предельная точка, граничная точка) и др.
Точка **
1) единица длины, применяемая главным образом в полиграфии и равная 0,351460 мм.
2) Русская единица длинны, применявшаяся до введения метрической системы мер (1точка = 1/100 дюйма = 1/10 линии = 254 мкм).
____________________________
* Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков, А.П.Ершов, Л.Д.Кудрявцев, А.Л.Онищик, А.П.Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил
** Политехнический словарь /Редкол.: А.Ю.Ишлинский (гл. ред.) и др. - 3 - е изд,, перераб. и доп. - М.: Советская энциклопедия, 1989. - 656 с. с ил.
Точка в ортогональной системе двух плоскостей проекций |
При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость является основание перпендикуляра, опущенного из данной точки на эту плоскость.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок. 7. Точка в системе двух плоскостей проекций |
|||
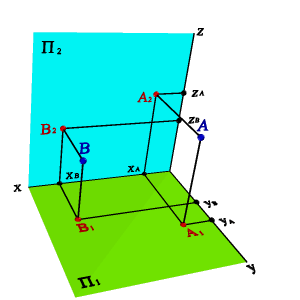
На рисунке 7 показана точка А и ее ортогональные проекции А1 и А2, которые называют соответственно горизонтальной и фронтальной проекциями.
Проекции точки всегда расположены на прямой, перпендикулярной оси x21 и пересекающей эту ось в точке А x.
Справедливо и обратное, т. е. если на плоскостях проекций даны точки А1 и А2 расположенные на прямой, пересекающей ось x21 в точке Аx под прямым углом, то они являются проекцией некоторой точки А.
На эпюре Монжа проекции А1 и А2 расположены на одном перпендикуляре к оси x21. При этом расстояние А1Аx - от горизонтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П2, а расстояние А2Аx - от фронтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П1.
Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 8 Точки в различных четвертях пространства |
|||
На рисунке 8 представлены точки A, B, C и D, расположенные в разных четвертях пространства и их эпюр (A - в первой, B - во второй, C - в третьей и D - в четвертой четвертях)
Точка в ортогональной системе трех плоскостей проекций |
В практике изображения различных геометрических объектов, чтобы сделать проекционный чертеж более ясным, возникает необходимость использовать третью – профильную плоскость проекций П3, расположенную перпендикулярно к П1 и П2. Плоскости проекций П1, П2 и П3 являются основными плоскостями проекций.
|
|
|
|
||
|
||
а) модель |
б) эпюр |
|
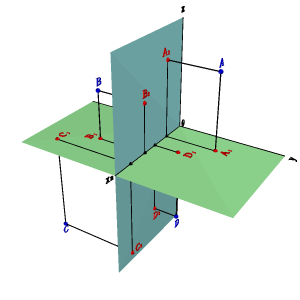
Рисунок 9. Точка в системе трех плоскостей проекций |
||
|
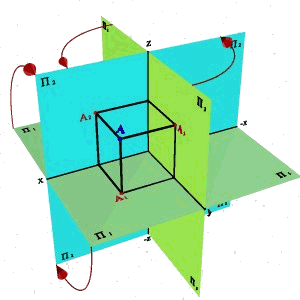
Модель трех плоскостей проекций показана на рисунке 9. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной. Проекции точек на эту плоскость обозначаются прописными буквами латинского алфавита или цифрами с индексом 3. Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают, как показано на рисунке 10, до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. |
Рисунок 10. Получение эпюра |
Координаты (от лат. со — совместно и ordinatus — упорядоченный, определенный) — числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. В 14 веке Н.Орем пользовался координатами на плоскости для построения графиков, называя долготой и широтой то, что теперь называют абсциссой и ординатой. Более систематически координаты стали применяться к вопросам геометрии на плоскости в 17 веке. Заслуга выяснения всего значения метода координат позволяющего систематически переводить задачи геометрии на язык математического анализа и обратно, истолковывать геометрически факты анализа, принадлежат Р. Декарту.
В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).
Положение точки относительно плоскостей проекций |
Положение точки в пространстве определяется тремя координатами x,y,z. Точка может занимать в пространстве как общее, так и частное положение по отношению к плоскостям проекций.
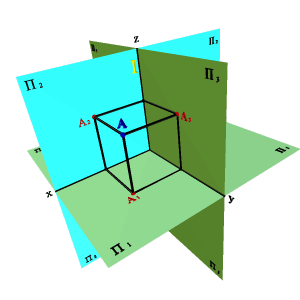
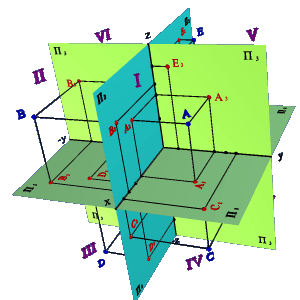
Точка не принадлежащая ни одной из плоскостей проекций - точка общего положения. Координаты точки общего положения не равны нулю (x≠0,y≠0,z≠0), и в зависимости от знака координаты точка может располагаться в одном из восьми октантов, как показано в таблице 1 и на рисунке 11.
|
|
Таблица 1 Знаки координат в октантах
|
||||||||||||||||||||||||||||||||||||||||||||||||
а) модель I-IV октантов |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
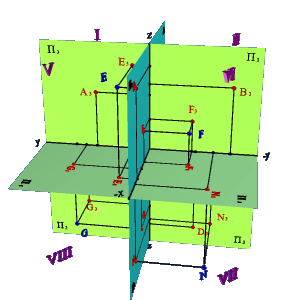
б) модель V-VIII октантов |
в) эпюр |
|||||||||||||||||||||||||||||||||||||||||||||||||
Рисунок 11. Точки общего положения |
||||||||||||||||||||||||||||||||||||||||||||||||||
Точка принадлежит плоскости проекций (рис.12).
Точка А принадлежит горизонтальной плоскости проекций (x≠0,y≠0,z=0) - фронтальная проекция точки лежит на оси x, а профильная на оси y.
Точка B принадлежит фронтальной плоскости проекций (x≠0,y=0,z≠0) - горизонтальная проекция точки лежит на оси x, а профильная на оси z.
Точка С принадлежит профильной плоскости проекций (x=0,y≠0,z≠0) - горизонтальная проекция точки лежит на оси y, а фронтальная на оси z.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 12. Точки частного положения |
|||
Точка принадлежащая одновременно двум плоскостям проекций - точка на оси (рис.12).
Точка D лежит на оси x, принадлежит одновременно горизонтальной и фронтальной плоскостям проекций (x≠0,y=0,z=0).
Точка E лежит на оси y, принадлежит одновременно горизонтальной и профильной плоскостям проекций (x=0,y≠0,z=0).
Точка F лежит на оси z, принадлежит одновременно фронтальной и профильной плоскостям проекций (x=0,y=0,z≠0).
Точка принадлежит одновременно трем плоскостям проекций - 0(x=0,y=0,z=0) - начало координат.
взаимное расположение точек |
Рассмотрим три основных варианта взаимного расположения точек, в зависимости от соотношения координат определяющих их положение в пространстве:
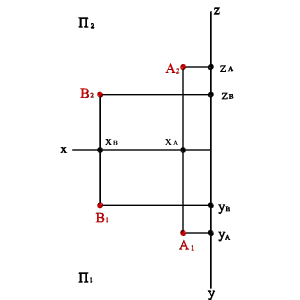
1. Рассмотрим точки А и В (рис.13), все три координаты которых отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций:
- YА>YВ. Тогда точка А расположена дальше от плоскости П2 и ближе к наблюдателю, чем точка В;
- ZА>ZВ. Тогда точка А расположена дальше от плоскости П1 и ближе к наблюдателю, чем точка В;
- XА<XВ. Тогда точка В расположена дальше от плоскости П3 и ближе к наблюдателю, чем (при взгляде слева) точка А.
|
|
|
|
|
|||
|
|||
а) модель |
б)эпюр |
||
Рисунок 13. Взаимное расположение точек |
|||
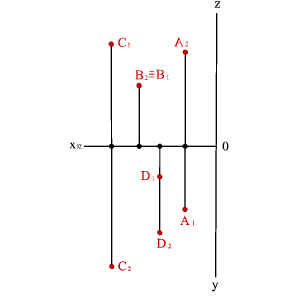
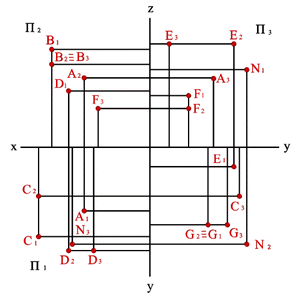
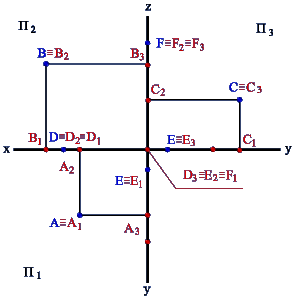
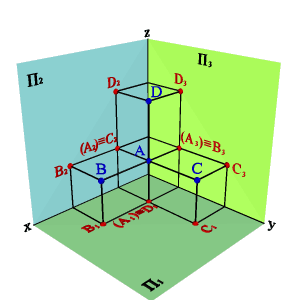
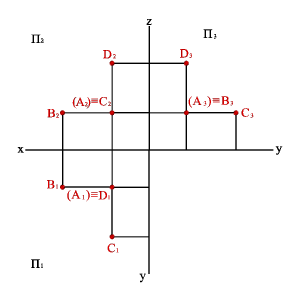
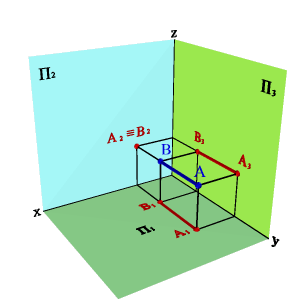
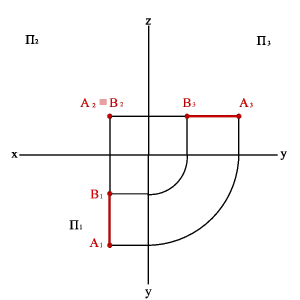
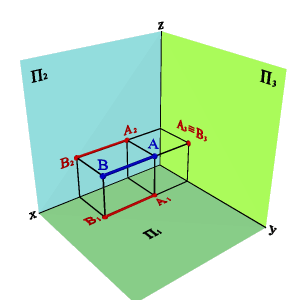
2. На рисунке 14 представлены точки А, В, С, D, у которых одна из координат совпадает, а две другие отличаются, их взаимное расположение можно оценить по удаленности к плоскостям проекций следующим образом:
– YА=YВ=YD, то точки А, В и D равноудалены от плоскости П2 и их горизонтальные и профильные проекции расположены, соответственно, на прямых А1В1//x12 и А3В3// z. Геометрическим местом таких точек служит плоскость, параллельная П2;
– ZА=ZВ=ZС, то точки А, В и С равноудалены от плоскости П1 и их фронтальные и профильные проекции расположены, соответственно, на прямых А2В2//x12 и А3С3// y. Геометрическим местом таких точек служит плоскость, параллельная П1;
– XА=XC=XD, то точки А, C и D равноудалены от плоскости П3 и их горизонтальные и фронтальные проекции расположены, соответственно, на прямых А1C1// y и А2D2//z . Геометрическим местом таких точек служит плоскость, параллельная П3.
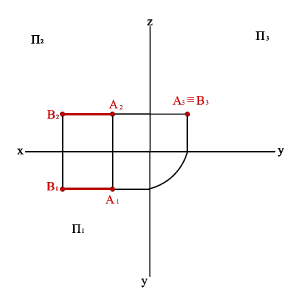
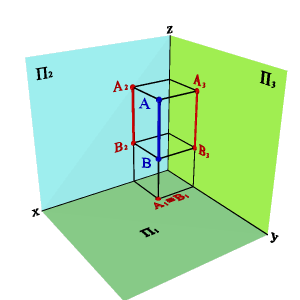
Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой. На рис. 14. даны три пары таких точек, у которых:
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 14. Конкурирующие точки |
|||
XА=XD;YА=YD;ZD>ZА;
XA=XC;ZA=ZC;YC>YA;
YA=YB;ZA=ZB;XB>XA.
Соответствующие проекции конкурирующих точек совпадают.
Различают: горизонтально конкурирующие точки А и D, расположенные на горизонтально проецирующей прямой АD ; фронтально конкурирующие точки A и C расположенные на фронтально проецирующей прямой AC; профильно конкурирующие точки A и B, расположенные на профильно проецирующей прямой AB.
При проецировании на соответствующую плоскость проекций одна точка «закроет» другую точку, конкурирующую с ней, соответствующая проекция которой окажется невидимой.
Прямая линия |
Прямая линия*- одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.
Прямая линия - алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением 1 - ой степени (линейное уравнение).
Общее уравнение прямой (полное):
Ах+Ву+С=0,
где А, В и С - любые постоянные, причем А и В одновременно не равны нулю. Если один из коэффициентов равен нулю, уравнение называется неполным.
Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил
Способы графического задания прямой линии |
Для определения положения прямой в пространстве существуют следующие методы:
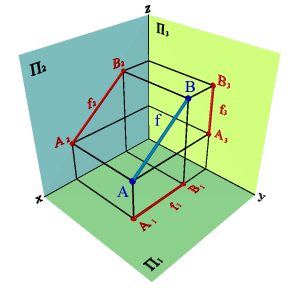
1.Двумя точками (а и в).
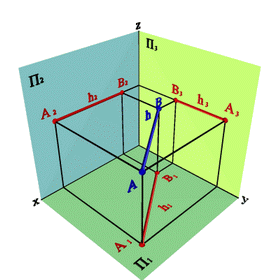
Рассмотрим две точки в пространстве А и В (рис. 15). Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [BA] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:
[A1B1]<[BA]; [A2B2]<[BA;] [A3B3]<[BA].
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 15.Определение положения прямой по двум точкам |
|||
Обозначим углы между прямой и плоскостями проекций через α- с плоскостью П1, β- с плоскостью П2, γ- с плоскостью П3 и тогда получим:
|А1В1|=|BA|cos a
|A2B2|=|AB|cos b
|A3B3|=|AB|cos g.
Частный случай |A1B1|=|A2B2|=|A3B3| при таком соотношении прямая образует с плоскостями проекций равные между собой углы a=b=g=350, при этом каждая из проекций расположена под углом 450 к соответствующим осям проекций.
2. Двумя плоскостями (a; b).
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
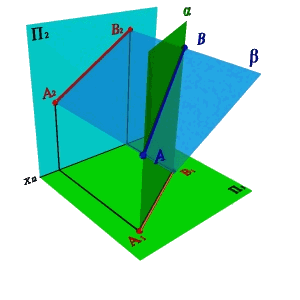
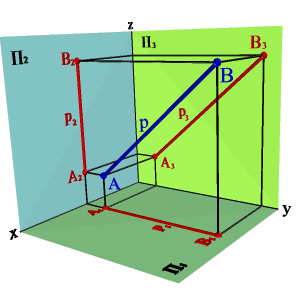
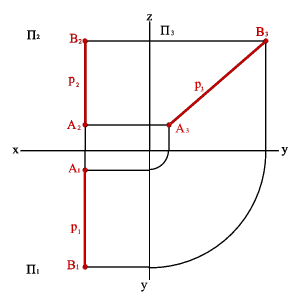
3. Двумя проекциями.
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.16а), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].
|
|
|
|
|
|
||
|
|
||
|
|
||
а) α непараллельная β |
б) α параллельная β |
||
Рисунок 16.Определение положения прямой в пространстве по двум проекциям отрезка |
|||
|
|
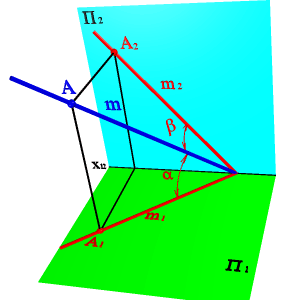
Плоскости a и b могут слиться в одну плоскость g, если, например, проекции [А1В1] и [А2В2] перпендикулярны оси x и пересекают ее в одной точке (рис.16б). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П2. 4. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве(рис.17). |
|
||
|
||
Рисунок 17. Определение положения прямой по точке и углам наклона к плоскостям проекций |
||
положение прямой линии относительно плоскостей проекций |
Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.18).
|
|
|
|
Рисунок 18. Прямая общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.19). Для любой пары точек горизонтали должно быть справедливо равенство
zA=zB Þ A2B2//0x; A3B3//0y Þ xA–xB≠0, yA–yB≠0, zA–zB=0.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 19. Горизонтальная прямая |
|||
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями (рис.20).
yA=yBÞ A1B1//0x, A3B3//0z Þ xA–xB≠0, yA–yB=0, zA–zB≠0.
|
|
||
а) модель |
б) эпюр |
|
|
Рисунок 20. Фронтальная прямая |
|
||
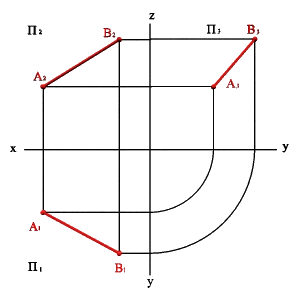
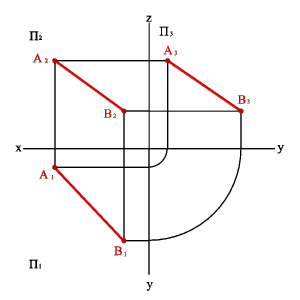
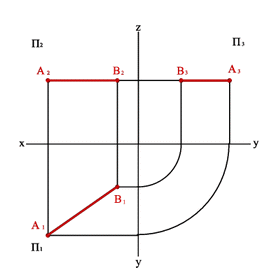
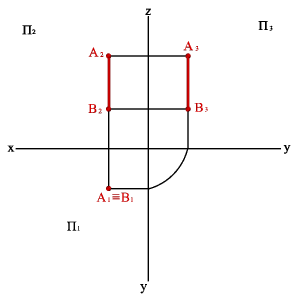
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 21).
xA=xB Þ A1B1//0y, A2B2//0z Þ xA–xB=0, yA–yB≠0, zA–zB≠0.
Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 21. Профильная прямая |
|||
3.1. Фронтально проецирующая прямая - АВ (рис. 22)
xA–xB=0ü
yA–yB≠0ý
zA–zB=0þ,
3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 22. Фронтально проецирующая прямая |
|||
3.2. Профильно проецирующая прямая - АВ (рис.23)
xА–xB≠0ü
yА–yB=0ý
zА–zB=0þ,
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 23. Профильно-проецирующая прямая |
|||
3.3. Горизонтально проецирующая прямая - АВ (рис.24)
xА–xВ=0ü
yА–yВ=0ý
zА–zВ≠0þ.
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 24. Горизонтально-проецирующая прямая |
|||
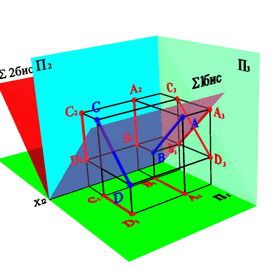
4. Прямые параллельные биссекторным плоскостям (рис. 25)
АВ //S1бис Þ xA–xB=0; zB–zA=yB–yA;
СD//S2бис Þ xС–xD=0; zD–zC=yC–yD.
Биссекторной плоскостью называется плоскость, проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П1 и П2 пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (S1бис), а через 2 и 4 четверти - второй (S2бис).
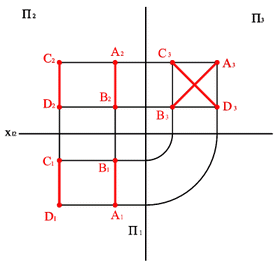
5. Прямые перпендикулярные биссекторным плоскостям (рис. 25)
АВ^S2бис Þ xA–xB=0; zB–zA=yВ–yА;
СD^S1бис Þ xС–xD=0; zD–zC=yC–yD.
|
|
|
|
|
|
|
|
||||
|
|
||||
а) модель |
б) эпюр |
|
|||
Рисунок 25. Прямые параллельные и перпендикулярные биссекторным плоскостям |
|
||||
следы прямой линии |
|||||
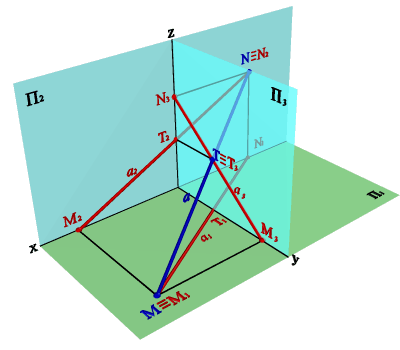
Следом прямой линии называется точка (рис. 26), в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю).
Горизонтальный след - М (zM=0)-точка пересечения прямой с горизонтальной плоскостью проекций.
Фронтальный след - N (yN=0)- точка пересечения прямой с фронтальной плоскостью проекций.
Профильный след - Т (xТ=0)- точка пересечения прямой с профильной плоскостью проекций.
|
|
|
|
а) модель |
б) эпюр |
||
Рисунок 26.Следы прямой линии в системе трех плоскостей проекций |
|||
Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N2N, а N1 лежит на оси x, N3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила:
1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью 0x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой.