
- •. Моделирование случайных дискретных событий.
- •2. Ответ (X)
- •3. «Выбор купонов»
- •I,box:cardinal;
- •3. В театре
- •3. Короткий кусок стержня.
- •Поправки к приближенным распределениям.
- •3. При бросании 100 монет какова вероятность выпадения ровно 50 гербов
- •Разделение области моделирования случайной величины.
- •3. Задача Сэмуэля Пепайса
- •Общая характеристика методов.
- •Метод Неймана.
- •Моделирование усеченных распределений.
- •Выбор равномерно распределенных точек в сложных пространственных областях.
- •3 Длина хорды
3. При бросании 100 монет какова вероятность выпадения ровно 50 гербов
procedure TForm1.Button9Click(Sender: TObject); //50 гербов
var
j,k:integer;
x:real;
begin
N:=StrToInt(Form1.LabeledEdit1.Text);
counter:=0;
i:=0;
while (i<N)do begin
j:=0;
k:=0; //количество гербов
while (j<100)do begin
x:=random;
if(x<0.5)then Inc(k);
Inc(j);
end;
if(k=50) then inc(counter);
Inc(i);
end;
otvet:=counter/N;
Form1.Edit1.Text:=FloatToStr(otvet);
end;
Билет №12
Разделение области моделирования случайной величины.
Этот прием иногда используют при моделировании случайной величины, плотность которой резко различна в различных областях.
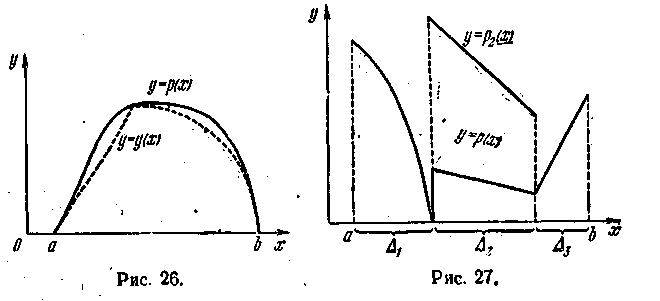
Пусть р(х)—плотность случайной величины ξ, определенной в интервале а < x < b. Разобьем этот интервал на сумму непересекающихся интервалов ∆k, так что (a, b) = ∆1 + … +∆m (рис. 27) и вероятности попадания ξ в ∆k положительны: сk = ∆k∫ p(x) dx > 0.
Введем в рассмотрение плотности
 p(x)
/ ck при x∆k,
p(x)
/ ck при x∆k,
pk(x) =
0 при x∆k,.
Очевидно, c1 + … +cm = 1 и при всех х из (а; b)
p(x) = c1p1(x) + … + cm pm(x).
Для того чтобы найти значение ξ, можно сперва по числу γ1 разыграть номер области η = k, а затем вычислить ξ из уравнения
 , (21)
, (21)
где ak – левый конец ∆k.
Легко проверить, что с точки зрения количества вычислений этот метод хуже, чем метод обратных функций.

можно решать следующим образом: сперва найдем номер k такой, что
k–1 k
∑ cj ≤ < ∑cj; (22)
j=1 j=1
тогда это уравнение превратится в уравнение
 (23)
(23)
решая которое и найдем ξ. Уравнение (23) проще, чем (21), и совпадает с уравнением модифицированного метода суперпозиции для рассматриваемой задачи.
Положение может резко измениться в пользу метода дробления области, если вместо (21) использовать для моделирования ξ с плотностью pk(х), в ∆k какой-нибудь другой способ. Правда, тогда на получение одного значения ξ будет затрачиваться больше двух случайных чисел.
Метод дробления области применим также для моделирования многомерных случайных величин [19].
2.

3. Задача Сэмуэля Пепайса
procedure TForm1.Button10Click(Sender: TObject); //Пейпас
var
c6,c12,c18,i,j,k:integer;
otvet,x:extended;
begin
N:=StrToInt(Form1.LabeledEdit1.Text);
j:=0;
c6:=0; c12:=0; c18:=0;
while (j<N)do
begin
k:=0;
for i:=0 to 5 do
begin
if random<(1/6) then inc(k);
end;
if(k>=1) then inc(c6);
k:=0;
for i:=0 to 11 do
begin
if random<(1/6) then inc(k);
end;
if(k>=2) then inc(c12);
k:=0;
for i:=0 to 17 do
begin
if random<(1/6) then inc(k);
end;
if(k>=3) then inc(c18);
j:=j+1;
end;
Edit1.Text:=('p6='+floattostr(c6/N)+' p12='+floattostr(c12/N)+' p18='+floattostr(c18/N));
end;
Билет №13
Общая характеристика методов.
Предположим,
что в
 мерном
пространстве переменных
мерном
пространстве переменных
 заданы случайная точка
заданы случайная точка
 с функцией распределения
с функцией распределения
 и некоторая область
и некоторая область
 .
Рассмотрим одномерную случайную величину
.
Рассмотрим одномерную случайную величину
 определенную формулой
определенную формулой
 при
при
 (36)
(36)
Для
расчета по этой формуле можно выбрать
случайную точку
 в пространстве; если
в пространстве; если
 то
вычисляется
то
вычисляется ;
если
;
если
 то точка
отбрасывается и выбирается новая. Таким
образом, при расчете по формуле (36) из
случайных точек
с функцией распределения
то точка
отбрасывается и выбирается новая. Таким
образом, при расчете по формуле (36) из
случайных точек
с функцией распределения
 отбирают
точки, принадлежащие
отбирают
точки, принадлежащие
 ,
и по ним вычисляют
,
и по ним вычисляют .
Мы будем говорить, что формула (36)
определяет метод отбора для моделирования
.
.
Мы будем говорить, что формула (36)
определяет метод отбора для моделирования
.
Эффективностью
метода отбора называют вероятность
отбора или, более подробно, вероятность
того, что точка
будет использована для расчета
,
а не будет отброшена. Очевидно,
эффективность метода (36) равно вероятности
 (37)
(37)
Выбрав

 точек
точек
 мы
получим в среднем всего
мы
получим в среднем всего
 значений
.следовательно,
на расчет каждого значения
затрачивается в среднем 1/э точек
.ясно,
что при малых э метод (36) становится
практически неэффективным.
значений
.следовательно,
на расчет каждого значения
затрачивается в среднем 1/э точек
.ясно,
что при малых э метод (36) становится
практически неэффективным.
Если
на реализацию каждой точки
затрачиваются
 случайных
чисел
случайных
чисел
 где,
очевидно,
где,
очевидно,
 то
в среднем на одно значение
затрачивается
то
в среднем на одно значение
затрачивается
 случайных чисел. В вычислительной
практике (при моделировании одновременных
величин
)
чаще всего встречаются случай
случайных чисел. В вычислительной
практике (при моделировании одновременных
величин
)
чаще всего встречаются случай
 и
и
 .
.
