- •. Моделирование случайных дискретных событий.
- •2. Ответ (X)
- •3. «Выбор купонов»
- •I,box:cardinal;
- •3. В театре
- •3. Короткий кусок стержня.
- •Поправки к приближенным распределениям.
- •3. При бросании 100 монет какова вероятность выпадения ровно 50 гербов
- •Разделение области моделирования случайной величины.
- •3. Задача Сэмуэля Пепайса
- •Общая характеристика методов.
- •Метод Неймана.
- •Моделирование усеченных распределений.
- •Выбор равномерно распределенных точек в сложных пространственных областях.
- •3 Длина хорды
3. В театре
procedure TForm1.Button7Click(Sender: TObject); //театр
var
i,j,boy,b1,g1,girl,pairs:cardinal;
otvet:extended;
x,y:extended;
begin
boy:=8;
girl:=7;
otvet:=0;
i:=1;
N:=StrToInt(Form1.LabeledEdit1.Text);
pairs:=0;
while (i<=N)do
begin
boy:=8;
girl:=7;
x:=random; // 1 mesto
if (x<boy/(boy+girl)) then
begin
dec(boy);
x:=0;
end
else begin
dec(girl);
x:=1;
end ;
for j:=2 to 15 do
begin
y:=random; // j-e mesto
if (y<boy/(boy+girl)) then
begin
dec(boy);
y:=0;
end
else begin
dec(girl);
y:=1;
end;
if ( (x+y)=1 )then
begin
pairs:=pairs+1;
end;
x:=y;
end;
i:=i+1;
end;
otvet:=pairs/N;
Form1.Edit1.Text:=FloatToStr(otvet);
end;
Билет №10
Моделирование n-мерной случайной точки с независимыми координатами. Если координаты n-мерной случайной величины Q=(ξ1, ..., ξn) независимы, то функция распределения
FQ(x1, ..., xn) = F1(x1)... Fn(xn),
где Fi(xi) – функция распределения величины ξi. Естественно ожидать, что в этом случае можно моделировать каждую величину ξi независимо:
Fi(ξi) = γi , i = 1,2, ...,n, (11)
где γi , ..., γn – независимые случайные числа.
Действительно, так как γi независимы, то и ξi определенные формулами (11), независимы. Поэтому их совместная функция распределения равна произведению
n n
Р{ξ1 < x1 ,... ,ξn <хп} = П Р{ ξi < xi} = П Fi(xi) = FQ(x1, ..., xn).
2.
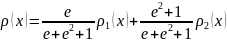
3. Короткий кусок стержня.
procedure TForm1.Button8Click(Sender: TObject); //короткий кусок стержня
var
short,long,x,y,l:real;
begin
N:=StrToInt(Form1.LabeledEdit1.Text);
l:=StrToFloat(Edit3.Text);
if (RadioButton1.Checked=true)then begin
short:=0;
i:=0;
while (i<N)do begin
x:=random*l;
if (x<(l/2)) then short:=short+x
else short:=short+(l-x);
Inc(i);
end;
otvet:=short/N;
Form1.Edit1.Text:=FloatToStr(otvet);
end; //checked1 отношение
if (RadioButton2.Checked=true)then begin
i:=0;
short:=0;
long:=0;
while (i<N)do begin
x:=random*l;
if (x<(l/2)) then
begin
short:=x;
long:=(l-x);
end
else
begin
short:=(l-x);
long:=x;
end;
y:=y+(short/long);
short:=0;
long:=0;
Inc(i);
end;
otvet:=y/N ;
Form1.Edit1.Text:=FloatToStr(otvet);
end;//checked-2 длина
end;
Билет №11
Поправки к приближенным распределениям.
Предположим, что плотность р(х) случайной величины ξ аппроксимируется снизу достаточно простой линией у(х). Очевидно, в качестве приближения к р(х) можно выбрать плотность
p1(x) = y(x) / c, где
b
c1 = ∫ y(x) dx, и находить приближенные значения ξ по плотности p1(x).
a
Можно, однако, представить р(х) в форме суперпозиции двух плотностей
p1(x) = y(x) / c1 и p2(x) = [p(x) – y(x)] / c2,
и получить таким образом метод для точного моделирования ξ. Алгоритм расчета ξ по плотности р(х) может оказаться весьма сложным; но на времени счета это почти не скажется, ибо р2(х) будет использоваться очень редко: Р{η = 2} = с2 = 1 – c1 << c1.
Итак, метод суперпозиции дает возможность учесть «поправку» p2(x), практически не увеличивая времени счета, а лишь ценою усложнения программы (впрочем, обычно это весьма нежелательно).
2.