Угол между плоскостями.

 

 

 

 

 Угол между двумя плоскостями в пространстве  связан с углом между нормалями к этим плоскостям ₁ соотношением:  = ₁ или  = 180⁰ - ₁, т.е.

cos = cos₁.

  Определим угол ₁. Известно, что плоскости могут быть заданы соотношениями:

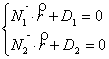, где

(A₁, B₁, C₁),  (A₂, B₂, C₂). Угол между векторами нормали найдем из их скалярного произведения:

.

  Таким образом, угол между плоскостями находится по формуле:

 

 Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

 

.

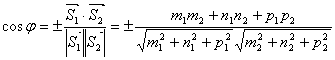Уравнение пучка плоскостей.

Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.

                                      рис.3.

Теорема. Пусть

 и 

– две плоскости, пересекающиеся по прямой L. Тогда уравнение

,    (10)

где   – произвольные действительные числа одновременно не равные нулю, есть уравнение пучка плоскостей с осью пучка L.

   Доказательство аналогично доказательству теоремы об уравнении пучка прямых и предоставляется читателю.

Пример. Найти уравнение пучка плоскостей, осью которого является ось абсцисс.

Решение. Очевидно, что координатные плоскости

 и   пересекаются по оси Ох.

         

                                              рис.4.

 Тогда уравнение (10) в данном случае принимает вид

. Заменив греческие буквы на латинские, получаем

                                     ,                                    (11)

где   – произвольные действительные числа, одновременно не равные нулю. Уравнение (11) есть искомое уравнение пучка плоскостей сосью пучка Ох.

   Аналогично, уравнение

                                     ,                                    (12)

есть уравнение пучка плоскостей с осью пучка Оу, а уравнение

                                                                          (13)

есть уравнение пучка плоскостей с осью пучка Оz.

2. Определение функции, способы задания функции, Возрастание и убывание функции. Четность и нечетность, периодичность функции.

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Познакоимимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].    Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении x от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности.  Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1).  Определение. Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1).  Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.

Функция может быть задана :