6. Агрегатная структура сложных систем. Полюсы и внутренние элементы. Виды связей между агрегатами системы.

Ответ:

Абстрактная теория структурных схем и блоков

Абстрактная теория структурных схем и блоков предполагает наличие простого блока (агрегата), для которого определены функциональные связи между входными и выходными сигналами: , где f _n-1 - входное множество сигналов, f_n - выходное множество сигналов, R – оператор связи.

Таким образом, простой блок (агрегат) можно представить в виде, показанном на рис. 1.14.

Рис. 1.14. Схема простого блока (агрегата)

Соединения блоков (агрегатов) приводят к появлению нового блока (агрегата) более высокого порядка, выполняющего более сложные функции.

Типовые наборы соединений блоков (агрегатов) следующие:

1. Последовательное соединение блоков

2. Параллельное соединение блоков

3. Замыкание обратной связью

Схема последовательного соединения блоков (агрегатов) представлена на рис. 1.15. Такая схема характерна для последовательного соединения триггеров. В результате формируется новый агрегат - двоичный счетчик импульсов.

Рис. 1.15. Схема последовательного соединения блоков (агрегатов)

Типовые параллельные соединения блоков (агрегатов) представлены на рис. 1.16.

Рис. 1.16. Схемы параллельного соединения блоков (агрегатов)

Схемы соединения блоков (агрегатов) с замыканием обратной связью приведена на рис. 1.17, где дано также формальное представление этого блока как нового агрегата.

Рис. 1.17. Схема соединения блоков (агрегатов) с замыканием обратной связью и её формальное представление

Множество R называется кольцом, если определены операции сложения и умножения с соблюдением правил коммутативности (перестановок) и ассоциативности (объединения).

Условие коммутативности: R₁+R₂= R₂+R₁ ; R₁R₂= R₂R₁.

Условие ассоциативности: (R₁+R₂)+R₃=R₁ +(R₂+R₃)+R₂;

(R₁R₂)R₂=R₁ (R₂R₃).

7. Принцип минимальности информационных связей агрегатов. Типичные структурные конфигурации. Структурный анализ информационных систем.

Ответ:

Объединение агрегатов в структурные элементы

Отдельные агрегаты могут объединяться и создавать структурные элементы системы.

Типовые наборы структурных элементов S_i приведены на рис. 1.13:

• последовательное соединение,

• параллельное соединение,

• каскадное соединение,

• соединение с обратной связью.

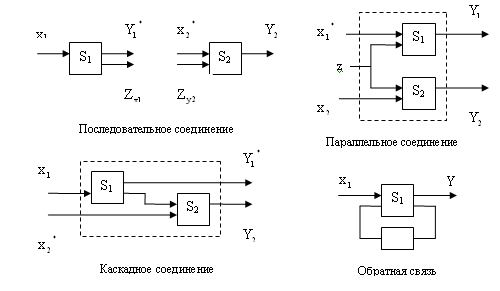
Рис. 1.13. Типовые соединения агрегатов в структурные элементы

Как правило, структурные элементы системы приобретают новые свойства по сравнению со свойствами отдельных агрегатов. Структурные элементы могут объединяться и создавать более сложные блоки и подсистемы, обладающие новыми свойствами и функциональными возможностями.

8. Анализ установившихся и неустановившихся режимов работы агрегатов. Нахождение случайного времени пребывания траектории агрегата в фиксированной области фазового пространства(12.2). Существование установившегося режима в кусочно-линейных агрегатах.

Ответ:

В настоящей главе будут рассматриваться и решаться некоторые задачи, возникающие при анализе агрегативных систем. Объектом рассмотрения всюду (если не сказано противное) будет автономный агрегат, вид которого (кусочно-линейный, кусочно-непрерывный и т. д.) будет всякий раз специально оговариваться.

Рассматриваемые в главе задачи относятся к двум типам. Решение задач первого типа характеризует в какой-то степени «неустановившийся» режим работы систем. Именно, в первом случае ищется функция распределения случайного времени первого выхода траектории процесса из фиксированной области фазового пространства. Решение таких задач имеет первостепенное значение прежде всего для теории надежности, когда искомая функция распределения есть не что иное, как «ненадежность» системы, если указанная область является множеством рабочих состояний. Если же эта область — множество отказо-вых (или «нежелательных») состояний, то задача сводится к оценке в статистическом смысле времени достижения системой «приемлемого» режима. Отметим аналогию между рассматриваемой задачей и практической устойчивостью (см. гл. 9).

Второй тип задач относится к «установившемуся» режиму системы, когда интересно знать финальное распределение состояний процесса. Кроме того, в задачах этого же типа обычно выясняются условия существования установившихся режимов. Постановка этих задач является традиционной для теории случайных процессов и имеет практическое значение для тех случаев, когда исследуемая система работает в течение достаточно длительного времени и интересуются некоторыми средними показателями ее работы за большой интервал времени. В гл. 15 будет установлена аналогия между устойчивостью по Лагранжу и рассматриваемой задачей. Аналогия эта (как и для случая практической устойчивости) будет подкреплена в гл. 15 использованием методов, «типичных» для теории устойчивости, применительно к указанным задачам.

В настоящей главе для решения этих задач будут использованы методы, более традиционные для теории случайных процессов.

В прикладных вопросах теории вероятностей и теории случайных процессов большое значение имеет факт существования установившегося или стационарного режима функционирования исследуемой системы. Для существования стационарного режима требуется, чтобы при любом начальном условии с течением времени вероятностное распределение состояний процесса (или некоторой функции от состояний) стремилось к распределению, не зависящему от выбранного начального условия.

Что это означает? Пусть мы рассматриваем некоторый случайный процесс z (t), значения которого принадлежат фазовому пространству Z. Если для каждого (измеримого) множества Г с Z существует предел

lim P [z (t)  Г/z (0) = z₀], не зависящий от z₀, то он и называется

t

стационарным или равновесным распределением процесса. Можно фиксировать не начальное состояние, а начальное распределение состояний.

Вполне понятно, что для существования у процесса функционирования системы предельного распределения необходимо на этот процесс наложить те или иные дополнительные условия. Как уже говорилось, свойство процесса иметь установившийся режим можно трактовать как своего рода устойчивость. Здесь же остановимся на том, как такой анализ для марковских процессов рассматриваемых типов, может осуществиться чисто «вероятностными» методами. Для этого потребуется ввести понятие «регенерирующий процесс», широко используемое в теории массового обслуживания и теории случайных процессов вообще (см. работы В. Л. Смита [15], В. Феллера [17]).

Вероятностный процесс z (t) называется регенерирующим, если существуют такие случайные моменты времени {t_i}, вообще говоря, определяемые предыдущим течением процесса, что величины _i = t_i — t_i-1, i  2, взаимно независимы, одинаковы распределены, а течение процесса z (t) при t > t_i не зависит от его предыстории, т. е. от течения z (t) при t  t_i. Величина ₁ независимая от _i, 2, может иметь распределение, отличное от распределений _i, i  2. Моменты t_i называются точками регенерации исходного процесса. Как нетрудно видеть, последовательность {_i }i>1 образует процесс восстановления. Развитие процесса после каждого момента не зависит от его предыстории и как бы начинается заново. Если с положительной вероятностью у процесса не наступает момента регенерации, то это означает, что функция распределения величины ₁ или _i, i  2, является несобственной. Более строгое и более общее определение регенерирующего процесса можно найти в уже упомянутой работе В. Л. Смита. Если z (t) является однородным, марковским процессом и если z*—некоторое фиксированное его состояние, то моменты возвращений процесса в это состояние являются точками регенерации процесса (в силу свойства марковости). Однако отнюдь не всякая точка обладает таким свойством, что время возвращения в нее конечно с вероятностью 1 и, тем более, среднее время возвращения конечно.

9. Исследование информационных систем, описанных в виде параллельных агрегативных систем.

Ответ:

10. Системы массового обслуживания, состоящие из бесконечного множества приборов(11.2). Предельное поведение системы массового обслуживания с бесконечно возрастающим числом приборов и загрузкой, стремящейся к критической.

Системы массового обслуживания, состоящие из бесконечного множества приборов

Рассмотрим известную формулу Эрланга — Севастьянова:

для вероятности занятости ровно k линий в телефонной системе с отказами; обозначает интенсивность входящего потока требований (предполагается, что этот поток простейший); — средняя длительность обслуживания; n — число обслуживающих приборов.

Пусть теперь n устремлено к бесконечности. Тогда для распределения числа занятых линий получим выражение

Рассмотрим распределение

Действительно, в бесконечнолинейной системе можно выделить n линий, на которые требования поступают в первую очередь. Для этих n линий они теряются, для системы же в целом остаются. Этим простым приемом установлено взаимно однозначное соответствие между реализациями процессов — числа занятых линий в момент t для системы с n линиями и системы с бесконечным множеством линий; при этом соответствии всегда , причем, очевидно, с положительной вероятностью при любом k 0 возможен случай, когда

В итоге получим

Одностороннюю оценку вероятности отказа n – линейной системы суммой вероятностей соответствующих состояний бесконечно линейной системы.

Пусть имеется система из бесконечного числа приборов; в нее поступает поток требований. В моменты времени, образующие нестационарный пуассоновский поток однородных событий интенсивности , поступают группы требований случайного объема. Обозначим через случайную величину, распределенную как число требований в группе, если эта последняя поступает в систему в момент t. Обозначим

Длительность обслуживания одного требования предположим случайной величиной с функцией распределения Н (х); длительности обслуживания разных требований будем считать независимыми в совокупности.

Обозначим через число требований в системе в момент t. Для нахождения распределения этой случайной величины применим следующий прием, облегчающий выводы такого рода. В любом отрезке (0, Т) нестационарный поток Пуассона является пределом при N -> (в смысле сходимости всех конечномерных распределений) потоков следующего вида. Отметим на интервале (0, Т) случайное число точек ( ) с помощью следующего механизма. Произведем N независимых испытаний. При каждом испытании в интервал (0, Т) может попасть лишь одна точка. С вероятностью она попадает в интервал , а с вероятностью она не попадает в (0, Т). Таким образом, суммарное число точек, попавших в интервал (0, Т), случайно, но не превышает N. Конечно, предполагается, что . С i-й точкой сопоставим группу требований, поступающих в i-й момент времени. Обозначим теперь через число требований в момент t из числа требований, поступивших в i-й момент времени . Очевидно, при при

t ; затем эта функция убывает единичными скачками по мере того, как требования обслуживаются, пока не обратится в нуль. Имеем

причем слагаемые этой суммы независимы в совокупности и одинаково распределены.

Загрузка  системы массового обслуживания определяется формулой  = /n, где  — интенсивность входящего потока;  — математическое ожидание длительности обслуживания; т — число приборов. Пусть т, 1; ищутся условия, при которых средняя длительность ожидания остается ограниченной. Здесь будет рассмотрена простейшая система массового обслуживания, распределения вероятностей состояний которой имеют простое аналитическое выражение. Из этого выражения непосредственно и будет получена предельная теорема. Отметим, что выводы, следующие из этой теоремы, по-видимому, будут иметь силу и в более общих ситуациях.

Теорема. Пусть имеется n-линейная система массового обслуживания с ожиданием; входящий поток — простейший с параметром Я; длительность обслуживания распределена по показательному закону с параметром 1. Тогда, если nи

=n-c

где с > 0 — некоторое фиксированное число, то средняя длительность ожидания требованием начала обслуживания в стационарном режиме сходится к 1/с при n.