Некоторые алгоритмы построения областей устойчивости в пространстве параметров
Обозначим
искомое множество через R, а пространство
параметров системы— через А. Множество
R описательно можно характеризовать
тем, что если значение параметров а
R, то процесс функционирования системы
обладает некоторым желаемым свойством.
Обычно при этом требуется, чтобы искомое
множество R являлось подмножеством
некоторой фиксированной области
А) —допустимой области изменений
параметров системы. Будем в дальнейшем
предполагать, что если задано значение
параметра а, то мы располагаем критерием,
позволяющим судить, принадлежит а
множеству R или нет. Так, если R — множество,
где значение некоторого функционала
ф(а) превышает значение ф0, то проверка
принадлежности а множеству R состоит в
вычислении (или оценке) конкретного
значения функционала и сравнении его
с ф0. Если R — область устойчивости по
Ляпунову решений обыкновенных линейных
дифференциальных уравнений, то можно,
например, проверить условия Гурвица в
точке а и т. д.
При исследовании реальных систем обычно известны некоторые априорные сведения относительно множества R. Такие сведения имеют, как правило, достаточно общий характер— односвязность R, гладкость ее границы, максимальная кривизна поверхности, выпуклость и т. п. Однако и они позволяют создавать специализированные алгоритмы нахождения множества R, учитывающие специфику имеющейся информации. Рассматриваемые ниже алгоритмы относятся к этому типу. Всюду будет предполагаться, что граница искомого множества достаточно гладкая и сведения об этой гладкости позволяют выбрать конкретное число точек и максимальное расстояние между ними, с достаточной степенью точности задающее искомое множество, поэтому на указанных вопросах останавливаться не будем.
Приведем
сначала алгоритм нахождения множества
R в двумерном евклидовом пространстве,
если известно, что множество R односвязно
и лежит в области
А. Пусть a1 и a2 — компоненты вектора a, a
= (a1 a2). Будем отмечать символом «+»
значения параметров, принадлежащие R,
а символом «—» — не принадлежащие R.
Результатом работы алгоритма является
фиксирование точек, лежащих в R и отстоящих
от границы R не далее, чем на заданное
число
> 0. Обозначим i-ю такую точку через
(с компонентами
и
,).
Работа алгоритма складывается из трех,
последовательно выполняемых этапов:
1)
поиск точек
(с компонентами
;
2)
нахождение точки
;
3)
обход границы множества R и фиксация
граничных точек
.
.
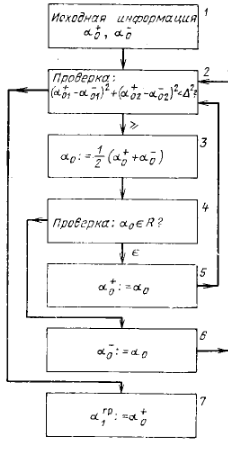
На
первом этапе ищутся две точки
После того как точки найдены , второй
этап – нахождение точки
,
лежащей на границе множества R.
На третьем этапе осуществляется обход
границы множества R,
начиная с найденной точки
.
При этом граница «нащупывается» с
помощью поисковых движений. Алгоритм
заканчивает свою работу, когда граница
множества замыкается. Очевидно, что
если
- ограниченная область, но алгоритм
завершит работу через конечное число
шагов.
Алгоритм может быть использован в случае, когда размерность вектора а превышает 2. Это осуществляется построением двумерных сечений множества R, когда все компоненты, кроме двух, фиксированы. Получая указанные сечения при различных значениях фиксированных компонент, можно найти все множество R. Правда при размерности вектора а уже более трех возникает проблема обозримости полученной информации координат граничных точек.
Путем неоднократного применения описанного алгоритма можно находить многосвязные и состоящие из нескольких односвязных множеств R, последовательно обходя различные границы.