- •3) Интегрирование простейших рациональных функций
- •5) Интегрирование тригонометрических выражений.
- •7) Основные свойства о.И.:
- •8) Формула Ньютона-Лейбница.
- •11. Численные методы интегрирования. Методы прямоугольников, трапеций и др.
- •12. Несобственные интегралы.
- •13. Общая схема построения определенного интеграла. Двойной и тройной интеграл и их свойства.
- •14. Геометрические приложения двойных и тройных интегралов и их вычисление повторным интегрированием.
- •1. Ду первого рода.
- •2. Дифференциальные уравнения с разделяющимися и разделенными переменными.
- •3. Линейные ду первого рода.
- •4. Численное решение дифференциального уравнения. Метод Эйлера.
- •5. Дифференциальные уравнения высших порядков. Общее и частное решение. Задача Коши. Теорема существования и единственности решения.
- •6. Линейный ду оператор n-го порядка и его свойства. Свайства решений линейного однородного ду. Фундаментальная система решений, определитель Вронского.
- •8. Линейные ду с постоянными коэффициентами и его характеристическое уравнение. Вид общего решения в зависимости от корней характеристического уравнения.
- •9. Методы отыскания частных решений линейных неоднородных уравнений. Метод Лагранжа и метод неопределенных коэффициентов.
- •10. Нормальная система ду. Общее и частное решение. Задача Коши. Теорема о существовании и единственности решения. Линейная система ду. Сведение ду n-го порядка к системе ду и наоборот.
- •11. Решение системы линейных однородных ду с постоянной матрицей.
- •2) Т. Подобия.
- •3) Дифференцирование оригинала.
- •4) Решение уравнений и систем операторным методом.
7) Основные свойства о.И.:
1.Если с – постоянное число и функция f(x) интегрируема на [a;b],то постоянный множитель можно выносить за знак О.И.
![]()
2.Если функции интегрируемы на [a;b], тогда интегрируема на [a;b] и их сумма, т.е. интеграл от суммы равен сумме интегралов.
![]()
3. Смена оценки снизу и сверху.
![]() ,
Из
ф.Н-Л.:
,
Из
ф.Н-Л.:
![]()
4. Аддитивности. Если функция f(x) интегрируема на [a;b] и a<c<b, то интеграл по всему отрезку равен сумме интегралов по частям этого отрезка:
![]()
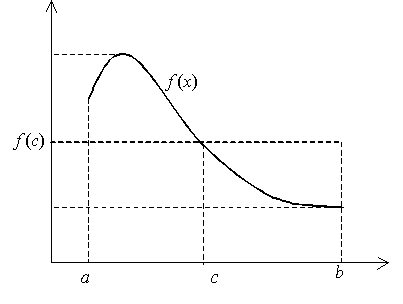
5.
«Т.
о среднем» Если функция f(x)
непрерывна на [a;b],
то сущ.(.) с є[a;b]
такая, что
![]() ,где
f(c)
– среднее значение функции f(x)
на [a;b].
,где
f(c)
– среднее значение функции f(x)
на [a;b].
Док-во:
По ф.Н-Л. Имеем:![]() ,где
F(x)-первообразная
f(x),т.е.
F’(x)=f(x).
Применяя к разности F(b)-F(a)
т.Лагранжа(т.о
конечном приращении функции), получим
F(b)-F(a)=F’(c)(b-a)=f(c)(b-a).
ч.т.д.
,где
F(x)-первообразная
f(x),т.е.
F’(x)=f(x).
Применяя к разности F(b)-F(a)
т.Лагранжа(т.о
конечном приращении функции), получим
F(b)-F(a)=F’(c)(b-a)=f(c)(b-a).
ч.т.д.
8) Формула Ньютона-Лейбница.
Т. Если функция y=f(x) непрерывна на отрезке [a;b] и F(x)-какая-либо ее первообразная на [a;b] (F’=f(x)),то имеет место формула:
Разобьём отрезок [a;b] точками a=x0,x1,…,xn=b на n частичных отрезков [x0;x1],..[xn-1;xn].
Рассмотрим тождество F(b)-F(a)=F(xn)-F(x0)=(F(xn)-F(xn-1))+…+ (F(x1)-F(x0)). Преобразуем каждую разность в скобках по формуле Лагранжа: F(b)-F(a)=F’(c)(xn-xn-1)+…+F’(c1)(x1-x0), т.е.
![]()
Переходя
от равенства к пределу при n→∞,
т.е. λ=max∆xi→0,получаем:
![]() .Ч.т.д.
.Ч.т.д.
Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интеграла заменена этим пределом:
![]() ,по
ф.Н.-Л.:
,по
ф.Н.-Л.:
![]() ,следовательно
,следовательно![]()
,т.е. О.И. с переменным верхним пределом есть одна из первообразных подынтегральной функции. Ч.т.д.
9)Интегрирование заменой переменной. Пусть для вычисления интеграла от непрерывной функции сделана подстановка x=φ(t).
Т. Если:
1. функция x=φ(t) и ее производная x’=φ’(t) непрерывны при tє[α;β];
2. множеством значений функции x=φ(t) при tє[α;β] является отрезок [a;b];
3. φ(α)=a и φ(β)=b,
то
![]()
Интегрирование по частям.
Т. Если функция u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a;b], то имеет место формула:
![]()
10)
Площадь плоской фигуры.
(*)Площадь криволинейной трапеции, расположенной «выше» оси абсцисс (f(x)≥0).
(**)Площадь криволинейной трапеции, расположенной «ниже» оси абсцисс (f(x)<0):
![]() (*);
(*); ![]() (**)
(**)
Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x), прямыми x=a и x=b (при условии f2(x)≥f1(x)) можно найти по формуле:
![]()

Длина дуги кривой.
Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y=f(x), где a≤x≤b.
Под
длиной дуги AB
понимается предел, к которому стремиться
длина ломанной линии, вписанной в эту
дугу, когда число звеньев ломаной
неограниченно возрастает, а длина
наибольшего звена стремиться к 0. Если
функция y=f(x)
и ее производная y’=f’(x)
непрерывны на отрезке [a;b],
то и кривая имеет длину, равную
![]()
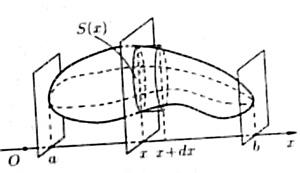
Объем тела по площади поперечных сечений.
Пусть требуется найти объем тела V, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S=S(x), a≤x≤b.
Тогда
объем тела можно найти по формуле:
![]()
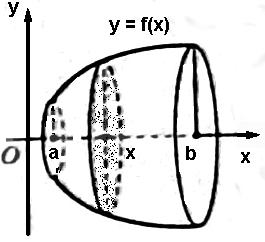
Объем тела вращения.
Пусть вокруг оси Ox вращается криволинейная трапеция, ограниченная линией y=f(x)≥0, отрезком a≤x≤b и прямыми x=a и x=b. Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох, есть круг радиусом y=f(x). Следовательно, S(x)= πy2. Применяя формулу объем тела по площади поперечных сечений, получаем
![]()