§3. Поверхность вращения.

П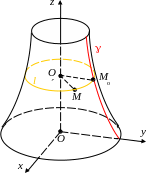 усть некоторая кривая  расположена в плоскости Oyz. Будем вращать ее вокруг оси Oz. Получим некоторую поверхность , которая называется поверхностью вращения. Каждая точка кривой  описывает окружность – параллель, центр которой лежит на оси Oz.

Пусть

(y, z) = 0 – (3)

уравнение кривой  в плоскости Oyz. Тогда в пространстве она задается системой

(y, z) = 0,

x = 0.

Пусть M(x, y, z) – произвольная точка поверхности . Тогда она лежит на одной из таких параллелей l и может быть получена поворотом точки M_o(0, y_o, z_o) =   l. Очевидно, что z_o= z (_*), и центр O параллели l имеет координаты O(0, 0, z). Кроме того, OM =OM_o . В координатах это условие имеет вид

y_o= . (_**)

Координаты точки M_o должны удовлетворять уравнению (3): (y_o, z_o) = 0. Подставляя сюда (_*) и (_**) получаем

(, z) = 0. (4)

Обратно, пусть координаты точки M(x, y, z) удовлетворяют (4). Тогда, если выполнено (_*) и (_**), то этому уравнению будут удовлетворять координаты точки M_o(0, y_o, z_o), а значит M_o. Кроме того, в силу (_*) и (_**) точка M_o лежит на одной параллели с M, а значит M может быть получена поворотом точки M_o вокруг оси Oz  M.

Итак, мы доказали, что (4) есть уравнение поверхности вращения . Таким образом, для того чтобы из уравнения кривой  получить уравнение поверхности вращения , мы в уравнении кривой оставляем без изменения координату z, а y заменяем: y  .

Обратно, если в уравнении поверхности можно выделить , и при этом, нигде более координаты x и y в уравнение не входят, то мы сразу можем сделать вывод, что наша поверхность есть поверхность вращения вокруг Oz.

Пример 1. Пусть  – окружность в плоскости Oyz радиуса b с центром в точке A(0, a, 0)Oy, a > b. Будем вращать ее вокруг Oz. Получим поверхность, которая называется тором. Уравнение окружности в плоскости Oyz имеет вид:

(y – a)² + z ² = b².

Вращаем вокруг Oz. Поэтому z оставляем без изменений, а y заменяем:

y  :

( – a)² + z² = b².

Получили уравнение тора. Заметим, что тор не относится к поверхностям 2 порядка.

П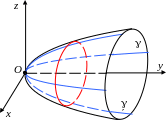 ример 2. Поверхность  задается уравнением

x² + z² = 2y.

Мы можем переписать его так:

()² = 2y.

Координаты x и z входят в уравнение только в выражении . Значит, наша поверхность – это поверхность вращения вокруг Oy. Для того, чтобы

получить уравнение кривой, которая вращается, мы заменяем на x и получаем уравнение кривой  в плоскости Oxy: x² = 2y. В пространстве эта кривая задается системой

x² = 2y,

z = 0.

Точно так же мы можем заменить на z и получить уравнение кривой  в плоскости Oyz: z ² = 2y. Вращая вокруг Oy первую или вторую кривую, мы получим одну и ту же поверхность.