Глава 3. Кривые второго порядка §1. Эллипс.

О пределение. Эллипсом называется множество точек  на плоскости, обладающее следующим свойством: существуют такие точки F₁, F₂, называемые фокусами, что сумма расстояний от произвольной точки M эллипса до F₁ и от M до F₂ есть величина постоянная:

 MF₁ + MF₂ = 2a = const, (1)

т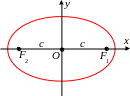 .е. независящая от выбора точки M, и 2a < 2c = F₁F₂ .

Составим уравнение эллипса в декартовых координатах. Начало координат поместим в середину отрезка F₁F₂, и направим OxOF1;\s\up10( –(. Тогда ось Oy определится однозначно. Фокусы будут иметь координаты F₁(c, 0), F₂(– c, 0).

Пусть M(x, y) – произвольная точка эллипса. Тогда

 MF₁ = ,  MF₂ = .

Согласно определению (1) имеем

= 2a – .

Возведем обе части равенства в квадрат и сократим одинаковые слагаемые:

x² – 2xc + c² + y² = 4a² – 4a + x² + 2xc + c² + y² .

4xc = 4a² – 4a  a = a² + xc.

Еще раз возводим в квадрат, сокращаем и группируем:

a²(x² + 2xc + c² + y²) = a⁴ + 2a²xc + x²c²,

x²(a² – c²) + a²y² = a²(a² – c²).

Согласно определению a < c; поэтому можем обозначить b² = a² – c² , и разделив на a²b², окончательно получаем

+ = 1 . (2 )

Мы доказали, что координаты произвольной точки эллипса удовлетворяют уравнению (2). Необходимо еще доказать обратное: если координаты точки M(x, y) удовлетворяют (2), то выполнено (1).

Из (2) выразим y² = b²(1– ) и подставим в выражение для  MF₁, учитывая при этом обозначение b² = a² – c²:

 MF₁ = = =

= =

= = = a – .

Аналогично получаем, что  MF₂ =a + . Из (2) следует, что  x   a (иначе уже первое слагаемое будет больше 1), а по определению, a < c  оба выражения под модулем неотрицательны. Поэтому

 MF₁ + MF₂ = a – + a + = 2a.

Уравнение (2) называется каноническим уравнением эллипса.

Геометрические свойства эллипса.

1. Из (2) следует, что  x   a,  y   b. Значит, эллипс целиком содержится в прямоугольнике, определяемыми этим неравенствами.

Подчеркнем, что это и все другие свойства выводятся только из уравнения эллипса, без ссылки на наглядность чертежа. Поэтому и раздел геометрии, который мы сейчас изучаем, называется «Аналитическая геометрия».

2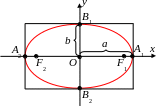 . Координатные оси пересекают эллипс в точках A₁(a, 0), A₂(– a, 0), B₁(0, b), B₂(0, – b), которые называются его вершинами. Отрезки A₁A₂ и B₁B₂ называются большим и малым диаметрами эллипса, а вместе – главными диаметрами. Числа a и b называются большой и малой полуосями.

3. Координатные оси являются осями симметрии эллипса, а начало координат – центром симметрии.

Действительно, пусть M(x, y) – произвольная точка эллипса. Тогда

п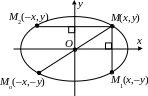 ара (x, y) удовлетворяет уравнению (2). Но тогда этому уравнению удовлетворяют также и пары (x, – y), (– x, y), (– x,– y), которые задают точки, симметричные M относительно Ox, Oy и точки O соответственно.

4. Эллипс может быть получен из окружности

: X ² + Y ² = a² (_**)

в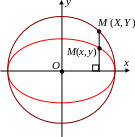 результате равномерного ее сжатия вдоль оси Oy с коэффициентом k = a/b. Действительно, при таком сжатии точка M (X, Y)  будет переходить в точку M(x, y), где

x = X , X = x ,

y = Y . ^ Y = y .

Подставляя последние формулы в (_**), получим, что координаты точки M удовлетворяют (2), т.е. M  .

5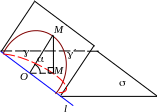 . Эллипс может быть получен из окружности в результате проекции окружности на плоскость  непараллельную плоскости окружности (;\s\up6(–. Действительно, при такой проекции отрезки параллельные линии пересечения плоскостей l =   (;\s\up6(– сохраняют длину, а отрезки перпендикулярные l сжимаются в 1/cos  раз, где  – угол между  и (;\s\up6(–. Таким образом, окружность сжимается по одному направлению, и согласно свойству 4, из нее получается эллипс.

6. Самостоятельно убедитесь, что параметрические уравнения эллипса имеют вид:

x = a cos  ,

y = b sin  , t R .