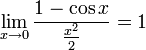1. Основні операції математики змінних величин на прикладі задачі про прямолінійний нерівномірний рух

1. Дано S(t) , знайти v(t) .

S = S(t+∆t)−S(t)

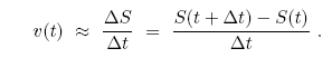
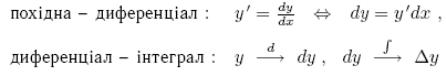
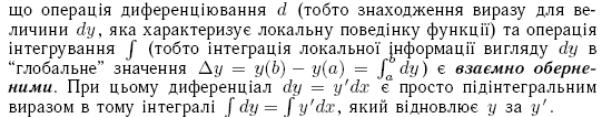
2. Повнота множини дійсних чисел. Теорема про вкладені відрізки.

3. Віддаль на числовій прямій. Розширена числова пряма.

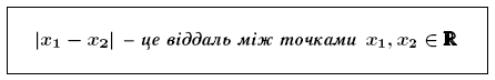
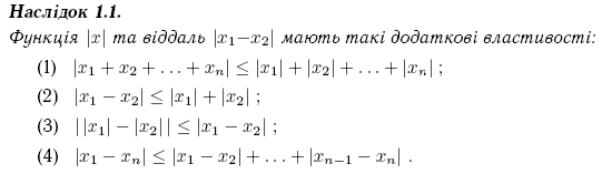
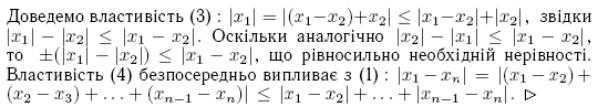
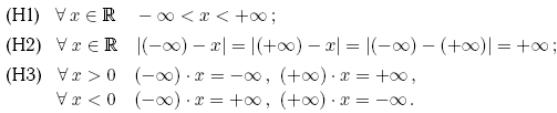
4. Околи та їх загальні властивості.

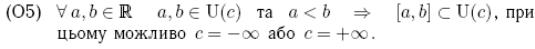
5. Обмеженість та точні межі числових множин: означення та існування точних меж, загальна теорема про повноту, характеристика обмеженості множини через точні межі.

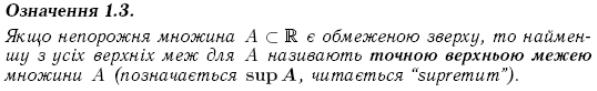
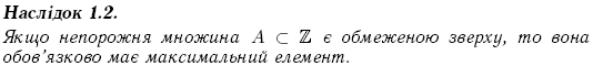
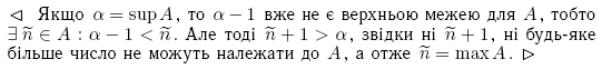
6. Комплексні числа: означення, алгебраїчні операції, геометричне зображення

Комплексне додавання та множення виразів а+0і рівносильно дійсному додаванню та множенню

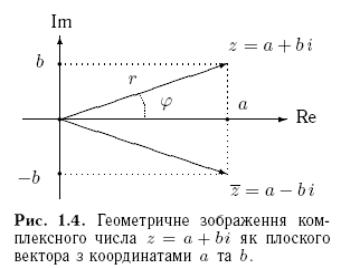
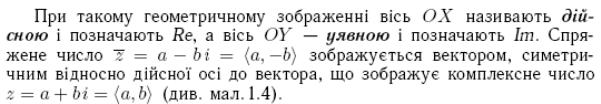
7. Комплексні числа: тригонометрична форма та її застосування

9. Границя послідовності та функції: загальні означення ті їх частинні випадки, приклади, критерій існування двосторонньої границі через односторонні

П

10. Єдиність границі послідовності та функції; зауваження про збіжні та нескінченно малі величини

11. Граничні оцінки та границі нерівностей для послідовностей та функцій

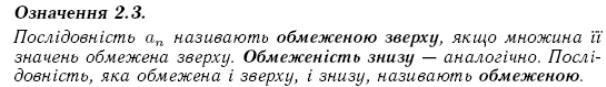
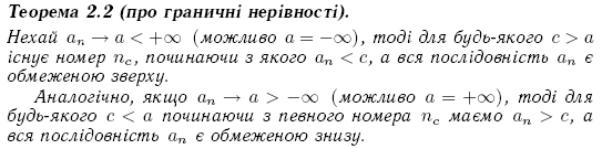
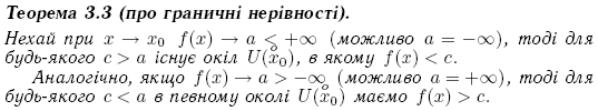
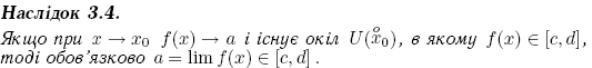
12. Границя затиснутої послідовності та функції

13. Границя суми, різниці, добутку й частки (для послідовностей та функцій).

14. Частинні границі послідовності: означення, існування границі послідовності через підпослідовності. Т-ма Больцано-Веєрштрасса.

15. Теореми про границю монотонних послідовностей та функції; їх наслідки

16. Число е та відповідна визначна границя

17. Критерій Коші збіжності послідовності та існування скінченної границі функції. Приклади збіжної та розбіжної послідовності.

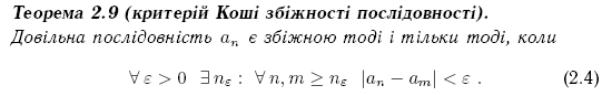
18. Теорема існування границі функції через послідовності

19. Неперервність функції: означення, збереження неперервності при арифметичних операціях над функціями та при суперпозиції, точки розриву та їх типи; приклади

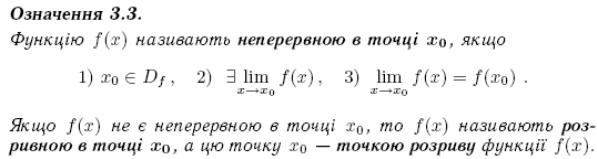
20. Елементарні функції та їх неперервність

21. Визначні границі.

Перша границя.

Доказательство

Рассмотрим односторонние пределы и и докажем, что они равны 1.

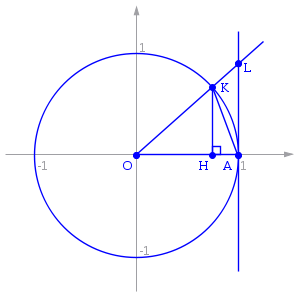
Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(1)

(где S_sectOKA — площадь сектора OKA)

(из : | LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

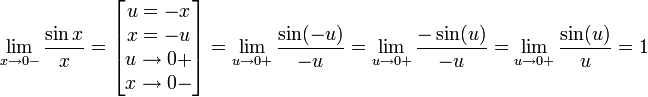
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

Доказательство следствий  [показать]

[править] Второй замечательный предел

или

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  [показать]

   Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где  — это целая часть x.

Отсюда следует: , поэтому

.

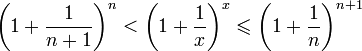Если , то . Поэтому, согласно пределу , имеем:

.

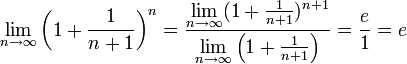
По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что для вещественного x.   

Следствия

1. 

2. 

3. 

4. 

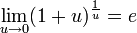
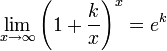
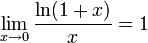
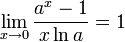5. для ,

6. 

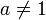
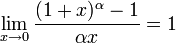
22. Асимптотична поведінка ф-ції: означення, основна теорема про асимптотичний розклад, наслідки.

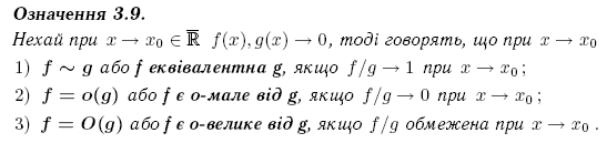
23. Властивості о-малих та застосування еквівалентностей до обчислення границь.