Тема 4: Понятия

Занятие 4

Понятием называется такая форма мышления, которая отражает в мозгу человека общие, существенные, отличительные (специфические) свойства (признаки) объектов и явлений действительности. Существенными свойствами и связями являются те, при помощи которых предметы и явления одного класса отличаются от предметов и явлений другого класса, являются общими для данного класса. Математические понятия отражают в мозгу человека пространственные формы и количественные отношения действительного мира. Отличаются высокой ступенью абстракции и обобщения, с развитием науки они развиваются, изменяются и совершенствуются.

Находясь в известных отношениях друг с другом, понятия каждой науки образуют определенную систему. Один и тот же раздел школьного курса математики может строиться с помощью различных систем понятий.

Изучить понятие – значит усвоить его содержание и объем. Содержание понятия – это множество всех его существенных признаков.

Содержание понятия раскрывается через определение. определением понятия является связное предложение (речевое или символическое), содержащее перечисление характеристических признаков понятия.

Понятие может быть определено различными способами:

1) через ближайший род и видовые отличия; 2) в математике существуют первоначальные неопределяемые или основные понятия, такие как множество, натуральное число, точка, прямая; их содержание устанавливается с помощью косвенного определения через абстракцию; 3) аксиоматическое определение (строгое определение); 4) разновидностью родовидовой формы определения являются: а)генетическое (конструктивное) определение – вместо характеристического свойства указывают процесс образования (происхождения) определяемого объекта (указание способа построения) (например, тела вращения); б) индуктивное определение, в котором указывают способ получения каждого следующего элемента определяемого класса объектов из каких-либо исходных его элементов.

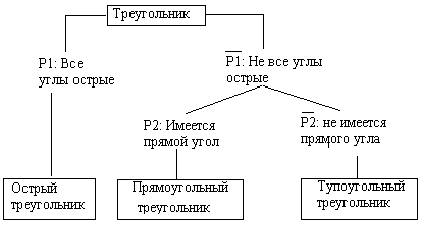
Детальное изучение объема понятия часто осуществляется с помощью классификации. Классификация обычно представляет собой последовательное разбиение множества на два класса с помощью некоторого свойства (называемого основанием классификации). Возможная схема классификации треугольников по величине угла приведена на рисунке.

Существуют различные виды определений. Часто все определения делятся на два вида: явные и неявные. Явными называются определения, в которых смысл определяемого термина полностью передается через смысл определяющих терминов. В неявных определениях смысл определяемого термина не передается полностью определяющими терминами. Типичный пример неявного определения – определение исходных понятий с помощью системы аксиом. Определение параллелограмма относится к числу явных.

Объем понятия раскрывается через классификацию. Объем понятия – это множество всех объектов, охватываемым данным понятиям. Определение классификации сформулированы на предыдущем занятии. Некоторые из них можно перефразировать как следствия для классификации понятий: а) понятия, получающиеся в результате классификации, должны быть взаимно независимы; б) в процессе классификации необходимо переходить к ближайшему в данном родовом понятии виду; в) сумма объемов понятий, получающихся при классификации, должна равняться объему исходного понятия

Вместе с классификацией полезно составлять родословную понятия – построение логического "дерева" его происхождения. Например, родословная понятия "плоский многоугольник": 1) плоскость, многоугольник; 2) простая ломаная, замкнутая ломаная; 3) ломаная; 4) фигура, точка, отрезок; 5) прямая, точка лежит между двумя точками.

Формирование у учащихся математических понятий одна из важнейших задач математического образования.

Три этапа формирования понятий: 1) используются методические приемы создания проблемной ситуации, в результате изучения которой происходит выявление, анализ и сравнение общих и существенных признаков некоторых объектов; 2) проводится работа над определением понятия. Умение дать правильное определение понятию – один из критериев его усвоения; 3) установление и развитие связей и отношений нового понятия с другими, способствующие усвоению всей системы понятий данной математической теории и математической дисциплины в целом.

В методике преподавания математики выделяют два метода введения понятий: конкретно-индуктивный и абстрактно-индуктивный. Схема применения конкретно-индуктивного метода такова: 1) анализируется эмпирический материал (при этом, кроме индукции, привлекаются и другие логические методы: анализ, сравнение, абстрагирование, обобщение); 2) выясняются общие признаки понятия, которые его характеризуют; 3) формулируется определение; 4) определение закрепляется путем приведения примеров и контрпримеров; 5) дальнейшее усвоение понятия и его определения происходит в процессе их применения.

Схема применения абстрактно-дедуктивного метода такова: 1) формулируется определение понятия; 2) приводятся примеры и контрпримеры; 3) дальнейшее усвоения понятия и определения происходит в процессе их применения.

Одна из практических рекомендации психологии усвоения понятий состоит в необходимости варьирования несущественных признаков понятия (прин­цип варьирования). Это варьирование необходимо как при конкретно-индуктивном, так и при абстрактно-дедук­тивном методе. Отсутствие необходимых вариаций часто приводит к формированию неправильных представлений о понятии. Например, если на уроках в VI классе при по­строении прямой, проходящей через данную точку А пер­пендикулярно к данной прямой а, прямая все время выби­рается горизонтальной, то и в случае, когда она не является горизонтальной, ученики все равно про­водят перпендикуляр как вертикальную прямую. Варьирование .расположения прямой а на плоскости способствует формированию правильных представлений о данном понятии.