33.Первый замечательный предел. Второй зам. Предел.

значит sinx подобен х в точке х=0. е- натуральное число.

34. Теорема о сжатой ф-и.

Пусть в некоторой окрестности точки х0 ф-я у=f(x) заключена между ф-ей φ(х) и ψ(х). φ(х) ≤f(x)≤ ψ(х), φ(х)= ψ(х)= A, тогда f(x)=А.

35. Понятие непрерывности и точек разрыва. Классификация т. разрыва. Если lim f(x)=limf(x)=f(x0)? То ф-я называется непрерывной в точке х0. Если нарушается это ус-е, то ф-я терпит разрыв. Классификация: 1)limf(x)= limf(x)≠f(x0)- это разрыв 1го рода устранимый. 2) limf(x)≠limf(x)-это разрыв 1го рода-скачёк. 3)если хотя бы один из пределов бесконечен, то разрыв называется разрыв 2го рода - бесконечный.

36. Понятие производной ф-и. Её геометрич. и механич. смысл. Если при х→0 отношение у/ х стремиться к конечному или бесконечному пределу, то этот предел называется производной ф-ию lim y/ x= f’(x)(y’, dy/dx). Геометрич. смысл: Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. Скорость-это определение координаты по времени. В этом и заключается механический смысл производной. Предел   называется величиной мгновенной скорости движения в момент времени  .

38. Таблица производных

C’=0, ,sinx’ = cosx, cosx’=-sinx, , , , , , , , , , x’=1,

39. Теорема Ролля и Коши.

Т. Ролля. Если функция f(x) непрерывна в замкнутом интервале [a;b] и дифференцируема в открытом интервале (а;в) и выполняется ус-е f(b)=f(a) то между точками а и в, х=а и х=, сущ-ет хотя бы одна точка х=с, в которой выполняется f’c=0, a<c<b.

Т. Коши. Пусть f(x) и g(х) непрерывны в замкнутом промежутке [a; в] и дифференцируемы на (а;в) Тогда на интервале (a,b) найдётся точка с (a<с<b), в которой

40. Формула Лагранжа. Формулы Тейлора и Маклорена.

f(b) –f(a)= f’(c) (b-a) формула Лагранжа. Выведена из формулы Коши, если g(x)=x. F(x)= f(a) + x + +…+ -формула Тейлора

F(x)= f(0)+ -ф-ла Маклорена . выведена из ф-лы Тейлора, если а=0.

41. Правило Лопиталя и раскрытие неопределённости с его помощью.

Если функции φ(х) и g(x) дифференцируемы в некоторой окрестности в точке a и одновременно при x→a стремиться либо к 0, либо к ∞, то 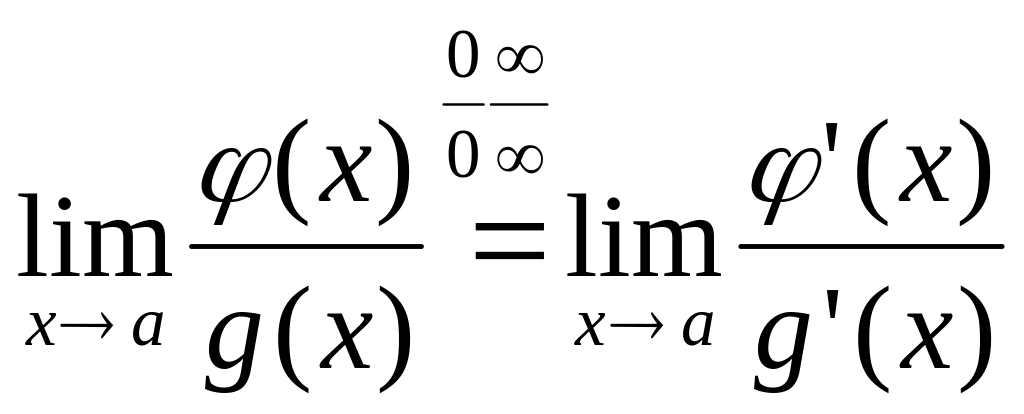применять можно несколько раз.

42. Необходимое и достаточное условие возрастания и убывания ф-и.

Необходимый признак: Если f(x) дифференц. и возрастает(убывает), то f ’(x) ≥ 0( f ‘ (x)≤0) . Достаточный признак : Если f ’(x)>0(f’ (x)<0), на промежутке , то ф-я возрастает(убывает).

43. Определение экстремума. Необходимое ус-е экстремума.

Экстр. ф-и – точка, в которой ф-я меняет промежуток возрастания на убывания и наоборот.

Необходимое ус-е: Если f(x) дифференц. в точке и имеет в этой точке экстремум, то f ’(x)=0 (обратное не верно)