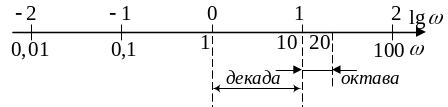Логарифмические частотные характеристики
Для приближенных инженерных расчетов удобно пользоваться не частотной характеристикой f(i) , а логарифмом от нее. Логарифмической амплитудной частотной характеристикой (ЛАЧХ) называется кривая l() = 20 lg (), построенная в логарифмическом масштабе по (Рис. 3.2). Единица измерения ЛАЧХ децибел. Отрезок на котором частота увеличивается вдвое, называется октавой, в 10 раз – декадой.
|
Рис. 3.2 Логарифмический масштаб |
Логарифмической фазовой частотной характеристикой (ЛФЧХ) называется кривая (), построенная в логарифмическом масштабе по .
3.3. Частотные характеристики элементарных звеньев
Найдем частотные характеристики элементарных звеньев из раздела 1.4, включая и звено запаздывания. Некоторые частотные характеристики изобразим на рисунках. Для определенности считаем, что коэффициент усиления k>1.
Усилительное звено f(p)=k.
На комплексной плоскости АФЧХ усилительного звена представляет собой точку на оси абсцисс с координатой k, т.е. сигнал любой частоты, проходя через усилительное звено, усиливается в k раз; при этом сдвиг фаз между входным и выходным сигналом отсутствует.
2) Интегрирующее звено
|
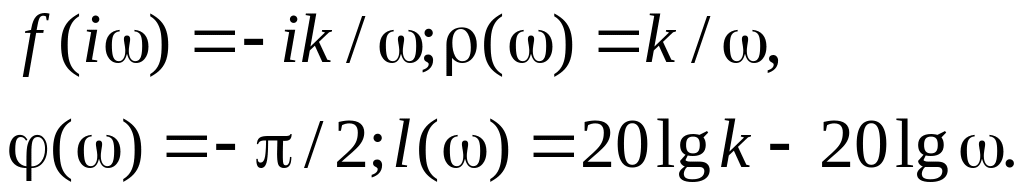
Рис. 3.3 АФЧХ и ЛАЧХ интегрирующего звена |
АФЧХ и ЛАЧХ
интегрирующего звена построены на рис.
3.3 как следует из левого графика и
формул (3.3), амплитуды периодических
сигналов, проходящих через интегрирующее
звено, уменьшаются в зависимости от
частоты по закону
.
Следует отметить, что интегрирующее
звено служит фильтром низких частот.
Частота
,
где график ЛАЧХ пересекает ось абсцисс,
называется частотой среза; очевидно,
.
Если частота входного сигнала равна
частоте среза, то амплитуды входного и
выходного сигнала одинаковы (
);
если
-
сигналы усиливаются (
);
если
-
сигналы ослабляются (
).
3) Устойчивое
апериодическое звено
.
Удобно ввести
безразмерную частоту
,
и строить частотные характеристики как
функции этой частоты
.
Функции
на
плоскости (
)
для
определяют
уравнение полуокружности, заданное в
параметрическом виде; исключив
получим явное уравнение для всей
окружности
.
|
Рис. 3.4 АФЧХ и ЛАЧХ устойчивого апериодического звена |
АФЧХ апериодического
звена построена на рис. 3.4 слева. Как
следует из формул , при
,
амплитуды выходных сигналов уменьшаются
по закону
,
а сдвиг фаз стремится к
.
Поэтому апериодическое звено также
является фильтром низких частот.
Для построения
ЛАЧХ апериодического звена рассмотрим
асимптотику функции
для
двух случаев:
Прямые ,
пересекаются в точке с абсциссой
;
частота
называется
сопрягающей частотой. Значение
функции
в точке
равно
поэтому ЛАЧХ апериодического звена
имеет вид, представленный на правом
рис. 3.4. Частота среза
4) Устойчивое
колебательное звено
.
Упражнение 5. Построить АФЧХ и ЛАЧХ для неустойчивого апериодического и колебательного звеньев.
5) Дифференцирующее звено
6) Форсирующее
звено первого порядка
;
7) Форсирующее
звено второго порядка
;
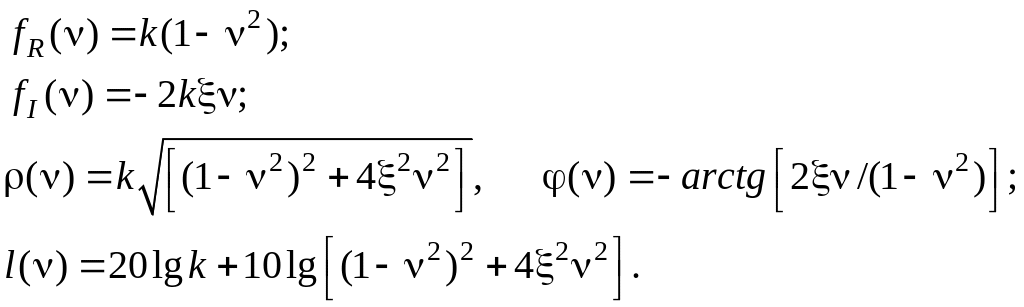
8) Звено запаздывания
АФЧХ звена запаздывания представляет собой окружность единичного радиуса.
Замечание. Для
интегрирующего апериодического и
колебательного звеньев фаза
,
т.е. выходной сигнал отстает от входного.
Для дифференцирующего и форсирующего
звеньев первого и второго порядков фаза
т.е. выходной сигнал опережает входной.
Упражнение 6. Построить АФЧХ и ЛАЧХ для форсирующих звеньев первого и второго порядков.