1.4. Элементарные звенья

Напомним, что блок (звено) САУ можно охарактеризовать с помощью его передаточной функции f(p) (см. рис 1.3). В дальнейшем будут использоваться звенья САУ, которые носят названия элементарных. Приведем передаточные функции элементарных звеньев:

1. Усилительное ;

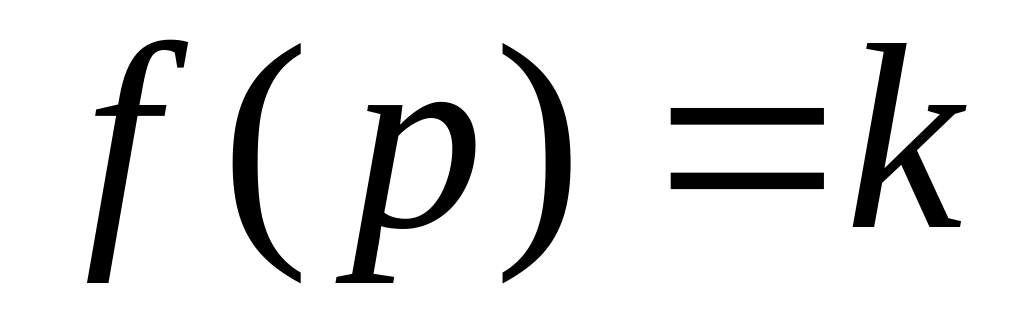2. Интегрирующее ;

3. Апериодическое ;

4. Колебательное , ,

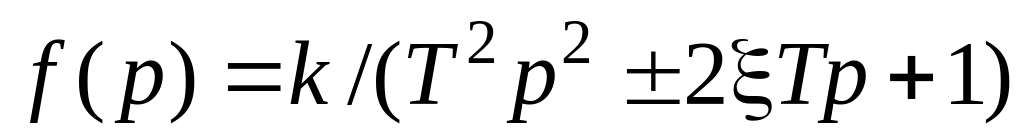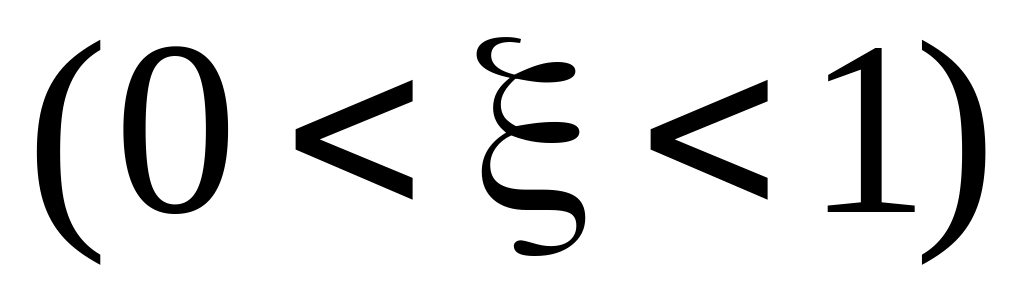5. Дифференцирующее ;

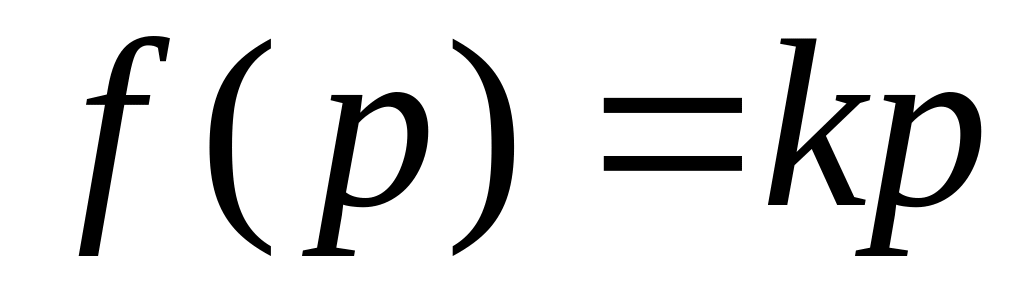6. Форсирующее первого порядка ;

7. Форсирующее второго порядка

, ;

Покажем, что любую дробно-рациональную функцию можно представить в виде произведения передаточных функций элементарных звеньев. Действительно, по теореме Гаусса (основная теорема алгебры) числитель b(p) и знаменатель a(p) разложим на произведение сомножителей вида ( ), где p_i - корни полиномов b(p), a(p). Если , то имеем либо интегрирующее звено (знаменатель) либо дифференцирующее звено (числитель); если действительное, то имеем либо апериодическое звено, либо форсирующее звено первого порядка. Пусть - комплексное; т.к. полиномы b(p),a(p) имеют действительные коэффициенты, то вместе с сомножителем входит сомножитель ( ), где - комплексно сопряженное к число. В этом случае получаем

,

поэтому имеем либо колебательное звено (знаменатель), либо форсирующее звено второго порядка (числитель).

Найдем переходные функции для некоторых из элементарных звеньев. Напомним, что при ; поэтому переходные функции достаточно строить при t>0.

1) Усилительное звено: .

2) Интегрирующее звено: .

3) Переходная функция апериодического звена находится из дифференциального уравнения

,

имеющее решение

.

Рис. 1.6. Приближенное представление дельта функции

График переходной функции устойчивого апериодического звена приведен на рис. 1.6. Посчитаем тангенс угла наклона касательной к кривой в начале координат.

.

Поэтому длина отрезка (см. рис. 1.6)

.

Величина T называется постоянной времени устойчивого апериодического звена и, как следует из рис.1.6, представляет собой характерное время, в течение которого переходная функция выходит на стационарный режим .

Согласно определениям раздела 1.3, посчитаем время переходного процесса

,

т.е. при выполнено .

Отметим, что переходная функция апериодического звена непрерывна, а ее производная в нуле терпит разрыв.

4) Построим переходную функцию устойчивого колебательного звена (1.13); для неустойчивого звена следует заменить на . Переходная функция определяется из дифференциального уравнения

; ; ,

которое имеет следующее решение:

; ; .

Заметим что условие эквивалентно наличию комплексных корней характеристического уравнения для .

Переходная функция устойчивого колебательного звена представлена на рис. 1.7, а соответствующие показатели качества переходного процесса таковы:

при ; при

Отметим что оценка времени переходного процесса огрублена т.е. существует такое, что при выполнено .

Переходная функция колебательного звена и ее производная непрерывны на всей числовой оси.

Упражнение 1. Получить формулы .

5) Дифференцирующее звено: , т.к. .

5’) В природе не существует объектов, которые можно описать идеальным дифференцирующим звеном . Реальные объекты инерционны и обладают запаздыванием. Рассмотрим реальные дифференцирующее звено с передаточной функцией переходная функция находится из уравнения

,

из которого следует, что переходная функция реального дифференцирующего звена равна импульсной переходной функции апериодического звена.

Для решения дифференциального уравнения проинтегрируем его левую и правую части в пределах от до t и введем новую переменную

.

С учетом свойства дельта-функции, получим уравнение для переменной

,

которое имеет решение . С учетом находим

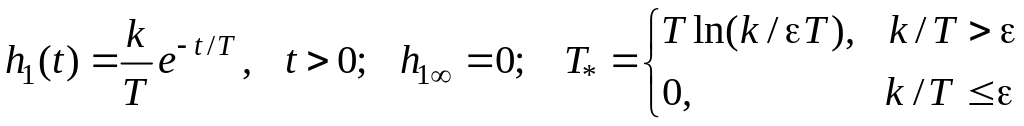
Переходная функция реального дифференцирующего звена имеет в точке t=0 разрыв 1 рода.

Упражнение 2. Посчитать импульсные переходные функции интегрирующего и колебательного звеньев.