Вопрос 1 Общее уравнение переноса

Смысл его в том, что скорость переноса чего-то (вещества, энергии...) пропорциональна градиенту того, что переносится, - градиенту концентрации вещества, градиенту плотности энергии и т. п.

Когда макросистема находится в равновесии, все ее тер-модинамические параметры постоянны по всему объему сис-темы. Если систему вывести из равновесия и предоставить самой себе, то она постепенно вернется в равновесное сос-тояние. При этом в системе будут протекать необратимые процессы, называемые процессами переноса. Различают нес-колько процессов переноса в зависимости от того, какие па-раметры системы были выведены из равновесия. Это – процессы переноса энергии, плотности и импульса, и свя-занные с ними явления теплопроводности, диффузии и вяз-кости. Процессы переноса возникают, когда имеется гради-ент какого-либо параметра макросистемы по всему объему макросистемы. При этом возникают потоки параметра в сто-рону уменьшения параметра.

Установление равновесия термодинамических систем происходит при помощи движения молекул. Это позволяет получить общее уравнение для всех явлений переноса.

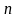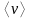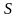Пусть имеется термодинамическая система с концен-трацией молекул, равной . Средняя скорость молекул . Движение молекул в такой системе будем считать полнос-тью хаотическим для того, чтобы не было направленных то-ков молекул и процессы переноса обусловливались только движением молекул. Возьмем некую площадку единич-ной площади. Определим плотность потока молекул, пере-секающих площадку в одном направлении. Пусть пло-щадка располагается перпендикулярно оси 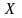. Плотность потока молекул, пересекающих площадку в положитель-ном направлении оси будет

. (2.1)

Этот поток и будет переносить физическую величину , выведенную из равновесия, в сторону уменьшения ее значе-ния. Плотность потока величины обозначим как . Предположим, что величина характеризует какое-то мо-лекулярное свойство одной молекулы, причем молекула об-ладала этим свойством на расстоянии свободного пробега 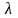от площадки . То есть последнее со-ударение молекула испытывала на расстоянии от площадки .

Пусть величина изменяется вдоль оси , т.е. имеет место градиент . Тогда возникает поток величины в сторону ее уменьшения (рис.2.1).

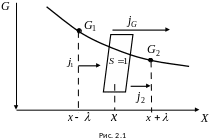
Тогда общее уравнение переноса для любой величины через площадку единичной площади, перпендикулярную на-правлению переноса, будет следующим:

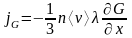, (2.2)

где – концентрация молекул,

– средняя скорость молекул,

– расстояние свободного пробега.

Значения этих величин берутся в сечении . Теперь на основе общего уравнения переноса получим уравнения для переноса массы, импульса и энергии…

Вопрос 2 Решетка с базисом на примере кубической объемно центрированной и кубической гранецентрированной решеток. Простая, объемно- и гранецентрированная кубические решетки

Обычно, знакомство с кристаллической структурой начинают с рассмотрения кубических примитивной, объемно- и гранецентрированной решеток (рис. 2.1), или, сокращенно, ПК, ОЦК, ГЦК.

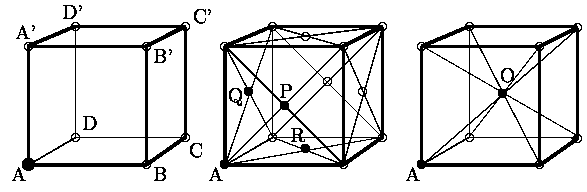
Рис. 2.1. Элементарные ячейки кубических решеток: а) простой; б) гранецентрированной; в) объемно--центрированной

Координаты узлов этих ячеек соответственно равны (Это как я понял и есть базис)

ПК	[[0, 0, 0]]
ОЦК	[[0, 0, 0]], [[1/2, 1/2, 1/2]]
ГЦК	[[0, 0, 0]], [[1/2, 1/2, 0]], [[1/2, 0, 1/2]], [[0, 1/2, 1/2]]

Билет 8