Вопрос 1 Сравнение механизма электропроводности металлов с механизмов проводимости в полупроводниках

Вопрос 2 Теплопроводность твердых тех

Теплопроводностью называется процесс переноса тепла от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры тела. В твердых телах, в отличие от жидкостей и газов, невозможна конвекция (передача тепла потоками нагретого вещества), поэтому перенос тепла осуществляется только за счет колебаний кристаллической решетки или с точки зрения квантовой теории за счет движения фононов. Если при данной температуре T один из узлов колеблется с амплитудой u, большей среднего значения  , то он, будучи связан с соседями силой межатомного взаимодействия, будет действовать на них, вызывая рост амплитуды колебаний соседних частиц. Таким образом, энергия передается от одного узла решетки к другому. Если концы твердого тела (например, стержня) поддерживаются при разных температурах, то в образце возникает непрерывный поток тепла. Каждый узел колеблется с меньшей амплитудой, чем соседний с ним со стороны более нагретого конца, и с большей амплитудой, чем соседний с ним со стороны менее нагретого конца.

Количественно тепловой поток  через поперечное сечение стержня   за время   пропорционален градиенту температуры   (закон Фурье):

,

(6.53)

где   коэффициент теплопроводности, который численно равен количеству тепла, прошедшего через единицу площади за единицу времени при градиенте температуры, равном единице (площадка   перпендикулярна оси x). В системе СИ размерность коэффициента теплопроводности составляет Вт/(мК), но часто используют размерности Вт/(смК) и кал/(смсК). Знак минус в формуле (6.63) показывает, что распространение тепла идет в сторону выравнивания градиента температуры (от более нагретой части тела к менее нагретой).

При низких температурах следует учитывать квантовый характер тепловых волн. Если  , то при теплообмене возбуждаются любые колебания в кристалле, все квантовые переходы возможны, и поэтому квантовый характер явления теплообмена не заметен. При низких температурах, когда  , в кристалле возбуждены лишь колебания с малыми частотами, и большие энергетические ступеньки не могут быть преодолены возникающими тепловыми «толчками». Рассмотрим процесс передачи тепла на основе представлений о фононах.

Из теории Дебая следует, что возбужденное состояние решетки можно представить как идеальный газ фононов, свободно движущийся в объеме кристалла. Фононный газ в определенном интервале температур ведет себя подобно идеальному газу, а поскольку фононы являются основными переносчиками тепла в твердом теле (это утверждение справедливо только для диэлектриков), то коэффициент теплопроводности твердого тела можно выразить такой же зависимостью, как коэффициент теплопроводности идеального газа

,

(6.54)

где   − теплоемкость единицы объема фононного газа,   − средняя длина свободного пробега фонона,   − скорость распространения звука в данном теле.

Вычисление средней длины свободного пробега фонона представляет собой сложную задачу, поскольку она зависит от того, на чем происходит рассеяние фононов: на других фононах, на дефектах структуры или на внешних гранях образца. Однако теоретический анализ приводит к тому, что при достаточно высоких температурах средняя длина свободного пробега фонона обратно пропорциональна абсолютной температуре. Поэтому коэффициент теплопроводности твердых тел при температурах выше характеристической ( ) обратно пропорционален абсолютной температуре.

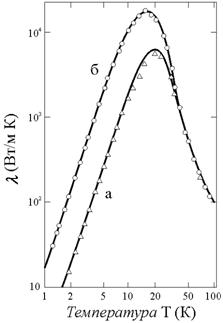
В достаточно чистых и бездефектных кристаллах при температуре, близкой к абсолютному нулю, возникает зависимость средней длины свободного пробега фононов от размеров образца. Это объясняется тем, что при низких температурах концентрация фононов мала, а следовательно, мала вероятность рассеяния фононов на других фононах. Пример зависимости коэффициента теплопроводности от температуры при различных сечениях образца монокристалла LiF показан на рис. 6.10 [98]. Видно, что различие в теплопроводности для образцов разного сечения проявляется только в области низких температур.

 

Рис. 6.10. Решеточная (фононная) теплопроводность как функция от температуры для монокристалла LiF при его различных сечениях: а  1,33  0,91 мм; б  7,55  6,97 мм

 

Полагая среднюю длину свободного пробега фононов приблизительно равной линейным размерам кристалла ( , где L − линейный размер кристалла), можно уравнение (6.54) переписать в виде

.

(6.55)

В правой части уравнения (6.55) от температуры зависит только теплоемкость единицы объема фононного газа . При температурах, близких к абсолютному нулю, теплоемкость пропорциональна   (закон   Дебая), поэтому и коэффициент теплопроводности  пропорционален кубу абсолютной температуры. Такой вывод подтверждается экспериментальными данными.

Анизотропия сил связи в кристаллах приводит к анизотропии коэффициента теплопроводности. Это можно проиллюстрировать на примере монокристалла кварца (рис. 6.11). В табл. 6.5 [52] представлены данные о коэффициенте теплопроводности по направлению, параллельному оси с, и по перпендикулярному к этой оси направлению.

 

 

Коэффициент теплопроводности вдоль гексагональной оси с кварца приблизительно вдвое выше соответствующих значений в направлениях перпендикулярных оси с, т. е. в направленииях, лежащих в базисной плоскости кристалла. С понижением температуры коэффициент теплопроводности возрастает, как и предсказывает квантовая теория.

Все вышесказанное относится к решеточной (фононной) части теплоемкости твердого тела, свойственной неметаллическим кристаллам. В металлах в переносе тепла, кроме атомов кристаллической решетки, участвуют еще и свободные электроны, которые одновременно являются и носителями электрического заряда, обеспечивая высокую электропроводность металлов. Более того, в чистых металлах основными носителями тепла являются именно свободные электроны, а не фононы. При достаточно высоких температурах металлов решеточная составляющая теплопроводности составляет всего 1−2 % от электронной теплопроводности. Этим объясняется высокая теплопроводность чистых металлов по сравнению с диэлектриками. Например, у алюминия при комнатной температуре коэффициент теплопроводности  = 2,26 10⁶ Вт/(смК), что приблизительно на два порядка больше, чем у кварца (см. табл. 6.5). Однако при очень низких температурах в металлах электронная часть теплопроводности меньше, чем решеточная. Это объясняется эффектами электрон-фононного рассеяния.

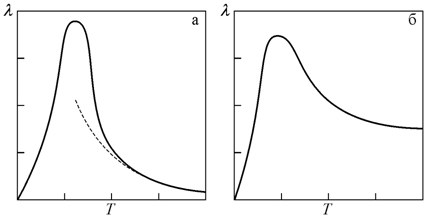
На рис. 6.12 приведен вид зависимости теплопроводности от температуры для диэлектриков и металлов.

 

Рис. 6.12. Сравнительные температурные зависимости коэффициента теплопроводности : а  для диэлектриков; б  для металлов [52]

 

В диэлектриках, практически не имеющих свободных электронов, перенос тепла осуществляется только фононами. Выше было сказано, что средняя длина свободного пробега   зависит от процессов рассеяния фононов на различных объектах. Все это приводит к тому, что температурная зависимость коэффициента теплопроводности  для диэлектриков имеет вид кривой с максимумом (рис. 6.12, а). Левая восходящая ветвь зависимости обусловлена увеличением числа фононов с ростом температуры, а правая нисходящая связана с ослабляющими фонон-фононным и другими видами рассеяния. Вид зависимости (T) для металлов (рис. 6.12, б) качественно похож на кривую для диэлектриков. Это связано с преобладанием при очень низких температурах фононного механизма теплопередачи. Однако с ростом температуры вклад фононной составляющей в этот процесс становится пренебрежимо мал и теплопередача осуществляется в основном свободными электронами. При относительно высоких температурах в металлах коэффициент теплопроводности  практически перестает изменяться с увеличением Т.

Билет 12.