4. Признаки Даламбера и Коши

Теорема. (Признак Даламбера) Пусть дан знакоположительный числовой ряд (7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство. По условию существует предел . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие или p-E< (10)

Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем … или

или (11)

Рассмотрим ряды (12) . (13)

Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.

Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется или u_n+1>u_n, то есть члены ряда возрастают с возрастанием номера n. Поэтому u_n¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.

Замечания.

1. Если расходимость ряда установлена с помощью признака Даламбера, то u_n¹0.

2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.

3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.

Пример.

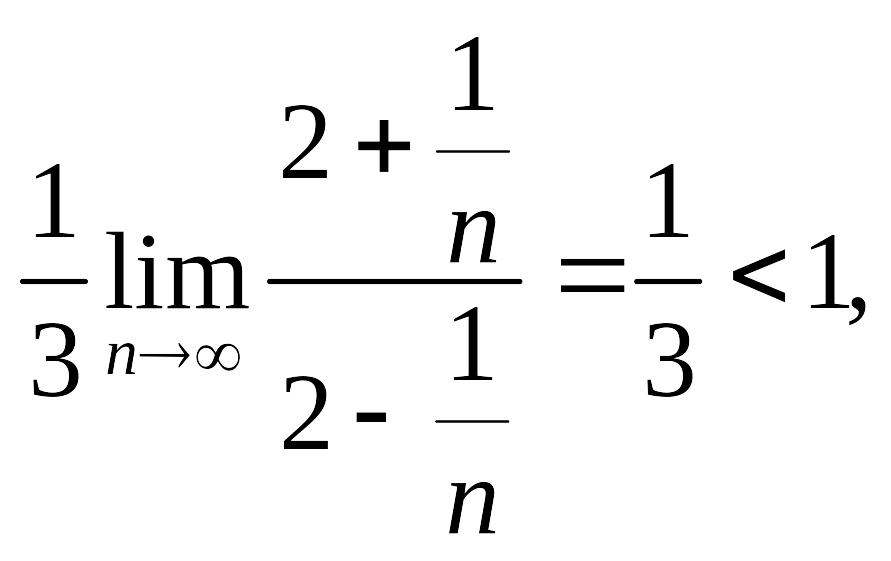Исследовать на сходимость ряд Применим признак Даламбера. u_n= u_n+1= . следовательно, ряд сходится по признаку Даламбера.

Теорема (Признак Коши)

Пусть дан знакоположительный числовой ряд u₁+u₂+…+u_n… (7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство. По условию существует Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | | <E или p-E< <p+E. (14)

Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <q или u_n<qⁿ для всех n³N. Рассмотрим ряды (15) (16)

Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что u_n<qⁿ для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).

Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или u_n>1, следовательно, u_n¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.

5. Интегральный признак сходимости

Теорема . (Интегральный признак Коши)

Пусть члены знакоположительного числового ряда u₁+u₂+…+u_n… (7) не возрастают: u₁³u₂≥…≥u_n≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, что f(1)=u₁, f(2)= u₂ ,…, f(n)= =u_n,… . Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом

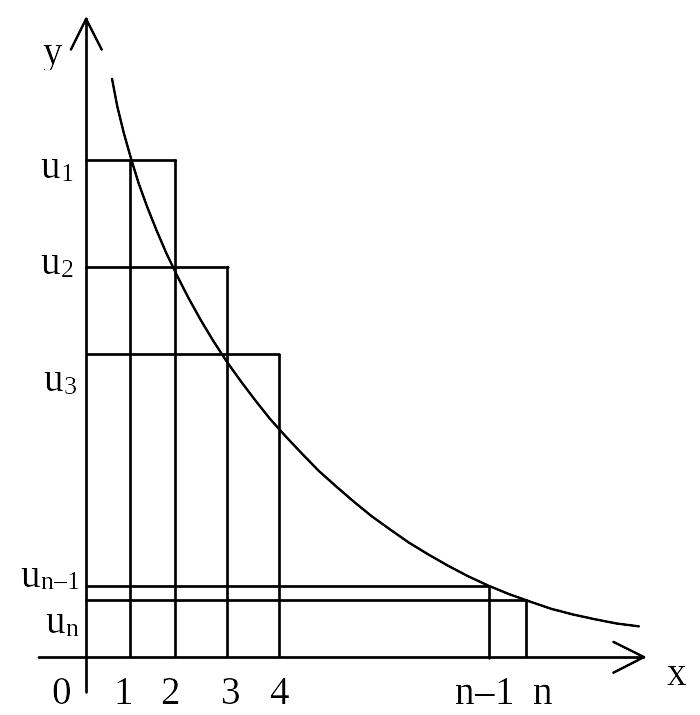
Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u₁,u₂,…,u_n-1, а также с высотами u₂,u₃,…,u_n.

S_n=u₁+u₂+…+u_n-1+u_n, S_впис=u₂^.1+u₃^.1+…+u_n^.1=u₂+u₃+…+u_n=S_n-u₁,

S_опис=u₁+u₂+…+ +u_n-1=S_n-u_n.

Площадь криволинейной трапеции S= . Получаем S_n-u₁< < S_n-u_n. Отсюда S_n<u₁+ (17)

и S_n>u_n+ (18)

Пусть сходится. Это означает, что существует конечный предел =Y. Соотношение (17) принимает вид: S_n<u₁+Y при любом n. Это означает, что последовательность частичных сумм S_n ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть расходится. Это означает, что =∞ и тогда из (18) следует, что последовательность частичных сумм S_n ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.

 

Пример.

Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд

Очевидно, f(x)= . При к≠1 имеем =

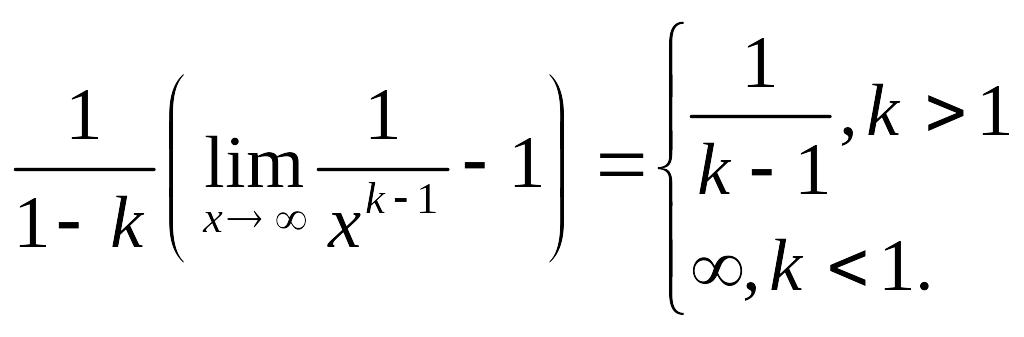
При к=1 имеем

Таким образом, обобщённый гармонический ряд сходится при k>1 и расходится при k≤1.