
- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
8. Действия над рядами
Действия с числовыми рядами
Выделяют следующие действия с числовыми рядами (они имеют смысл, т.е. сохраняют сумму ряда, только если она существует):
Линейная комбинация рядов
Если
ряды
![]() и
и
![]() сходятся,
то сходится и ряд
сходятся,
то сходится и ряд
![]() (α,
β — постоянные), при этом
(α,
β — постоянные), при этом
![]()
Группировка членов ряда
Сгруппируем слагаемые ряда , объединив без изменения порядка следования по нескольку (конечное число) членов ряда. Получим некоторый новый ряд . Раскрытие скобок в ряде в общем случае недопустимо, однако: если после раскрытия скобок получается сходящийся ряд, то раскрытие скобок возможно; если а каждой скобке все слагаемые имеют один и тот же знак, то раскрытие скобок не нарушает сходимости и не изменяет величину суммы.
Перестановка членов ряда
Если
ряд сходится абсолютно, то любой ряд,
полученный из него перестановкой членов,
также сходится абсолютно и имеет ту же
сумму, что и исходный ряд. Если ряд
сходится условно, то для любого наперёд
заданного A
(в том числе
![]() ,
,
![]() ,
,
![]() )
можно так переставить члены этого ряда,
что преобразованный ряд сходится к A
(расходится к
)
можно так переставить члены этого ряда,
что преобразованный ряд сходится к A
(расходится к
![]() ,
,
![]() ,
,
![]() )
либо не имеет предела (теорема Римана).
)
либо не имеет предела (теорема Римана).
9. Степенные ряды. Определение.
Определение Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: u1(x)+u2(x)+…+un(x)+… .
Определение. Если при x=x0 функциональный ряд сходится, то x0 называется точкой сходимости функционального ряда.
Определение. Множество всех точек сходимости функционального ряда называется его областью сходимости.
Очевидно, что в области сходимости функционального ряда его сумма является функцией от x. Будем обозначать её S(x).
Определение. Степенным рядом называется функциональный ряд вида
![]() , (24)
где
a,
a0,
a1,
a2,
…, an,
… – некоторые числа, называемые
коэффициентами степенного ряда.
, (24)
где
a,
a0,
a1,
a2,
…, an,
… – некоторые числа, называемые
коэффициентами степенного ряда.
10. Интервал сходимости степенного ряда. Теорема Абеля
Теорема (о структуре области сходимости степенного ряда)
Областью
сходимости степенного ряда (24) является
интервал (a-R;a+R),
к которому в зависимости от конкретных
случаев могут быть присоединены точки
a-R
и a+R,
где R=
![]() (если
этот предел существует). В каждой точке
интервала (a-R;a+R)
ряд сходится абсолютно.
(если
этот предел существует). В каждой точке
интервала (a-R;a+R)
ряд сходится абсолютно.
Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
|a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (25)
Применим
к ряду (25) признак Даламбера
![]()
![]()
Возможны три случая:
1.
Если
![]() или |x-a|<R
или xЄ(a-R;a+R),
то ряд (25) сходится, но тогда по достаточному
признаку сходимости знакопеременного
ряда сходится и ряд (24), причём абсолютно.
или |x-a|<R
или xЄ(a-R;a+R),
то ряд (25) сходится, но тогда по достаточному
признаку сходимости знакопеременного
ряда сходится и ряд (24), причём абсолютно.
2.
Если
![]() ,
то ряд (25) расходится. В этом случае
,
то ряд (25) расходится. В этом случае
![]() ,
то есть при достаточно больших n
|un+1|>|un|,
значит
,
то есть при достаточно больших n
|un+1|>|un|,
значит
![]() ≠0
и
≠0
и
![]() ≠0,
следовательно, ряд (24) расходится по
следствию из необходимого признака
сходимости. Теорема доказана.
≠0,
следовательно, ряд (24) расходится по
следствию из необходимого признака
сходимости. Теорема доказана.
Определение Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.
Замечание. Любой степенной ряд (24) сходится при x=a. Если других точек сходимости у ряда (24) нет, то считают, что R=0. Если степенной ряд (24) сходится во всех точках числовой прямой, то считают, что R=∞.
Примеры.
Найти
область сходимости степенного ряда.
1.
![]()
Составим
ряд из абсолютных величин членов данного
ряда
![]() и применим к нему признак Даламбера.
|un|=
и применим к нему признак Даламбера.
|un|=
![]() ,
|un+1|=
,
|un+1|=
![]() ,
,
![]() =
|x|.
=
|x|.
![]() |x|.
|x|.
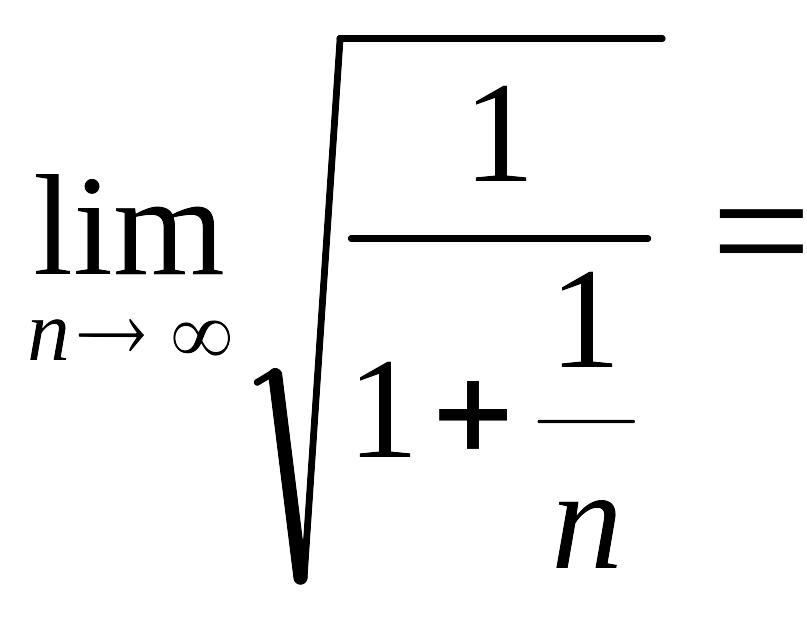 |x|.
|x|.
Ряд
сходится, если |x|<1
или x
![]() (-1;1)
– это и есть интервал сходимости.
Исследуем концы этого интервала. При
x=1
получаем расходящийся обобщённый
гармонический ряд
(-1;1)
– это и есть интервал сходимости.
Исследуем концы этого интервала. При
x=1
получаем расходящийся обобщённый
гармонический ряд
![]() .
При x=-1
получаем знакочередующийся числовой
ряд
.
При x=-1
получаем знакочередующийся числовой
ряд
![]() сходящийся по признаку Лейбница.
сходящийся по признаку Лейбница.
Действительно,
=
![]() и
|un|=
и
|un|=
![]() |un+1|=
|un+1|=
![]() Таким
образом, областью сходимости данного
ряда является промежуток [-1;1); R=1.
Таким
образом, областью сходимости данного
ряда является промежуток [-1;1); R=1.
2.
![]() Составим
ряд из абсолютных величин членов данного
ряда
Составим
ряд из абсолютных величин членов данного
ряда
![]() и
применим к нему признак Даламбера.
|un|=n!.|x-a|n,
|un+1|=(n+1)!.|x-a|n+1,
и
применим к нему признак Даламбера.
|un|=n!.|x-a|n,
|un+1|=(n+1)!.|x-a|n+1,
![]()
![]()
![]() Таким
образом, областью сходимости данного
ряда является одна точка x=a;
R=0.
Таким
образом, областью сходимости данного
ряда является одна точка x=a;
R=0.
3.
![]() Составим
ряд из абсолютных величин членов данного
ряда
Составим
ряд из абсолютных величин членов данного
ряда
![]() и применим к нему признак Даламбера.
|un|=
и применим к нему признак Даламбера.
|un|=
![]() |un+1|=
|un+1|=
![]()
![]()
![]() при всех x.
Таким образом, областью сходимости
данного ряда является промежуток
(-∞;+∞);
R=∞.
при всех x.
Таким образом, областью сходимости
данного ряда является промежуток
(-∞;+∞);
R=∞.
