
- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
1. Числовые ряды. Сходимость и расходимость числовых рядов
Определение ряда и его сходимость
Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,….
Выражение
![]() (1)
называется
числовым рядом. Числа u1,
u2,…,un,…
называются первым, вторым, …,
n-м,
… членами ряда. un
также называется общим членом ряда.
(1)
называется
числовым рядом. Числа u1,
u2,…,un,…
называются первым, вторым, …,
n-м,
… членами ряда. un
также называется общим членом ряда.
Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
![]()
Определение
3.
Если существует конечный предел
![]() то он называется суммой ряда (1), а ряд
(1) называется сходящимся. Если
то он называется суммой ряда (1), а ряд
(1) называется сходящимся. Если
![]() не существует или равен бесконечности,
то ряд (1) называется расходящимся и
суммы не имеет.
не существует или равен бесконечности,
то ряд (1) называется расходящимся и
суммы не имеет.
Простейшие свойства числовых рядов
Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,…. Выражение
(1) называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n-м, … членами ряда. un также называется общим членом ряда.
Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
Определение 3. Если существует конечный предел то он называется суммой ряда (1), а ряд (1) называется сходящимся. Если не существует или равен бесконечности, то ряд (1) называется расходящимся и суммы не имеет.
Теорема 1. Если сходится ряд, полученный из ряда (1) отбрасыванием нескольких его членов, то сходится и ряд (1). Обратно, если сходится данный ряд (1), то сходится ряд, полученный из ряда (1) отбрасыванием нескольких членов.
Другими словами: на сходимость ряда не влияет отбрасывание конечного числа его членов.
Доказательство. Пусть Sn – n-я частичная сумма ряда (1), Ck – сумма к отброшенных членов (заметим, что при достаточно большом n все отброшенные члены содержатся в сумме Sn), sn-k – сумма членов ряда, входящих в сумму Sn и не входящих в Ck. Таким образом:
![]() ,
где
Ck
– постоянное число, не зависящее от n.
,
где
Ck
– постоянное число, не зависящее от n.
Из
последнего равенства следует, что если
существует
![]() то существует и
и обратно, если существует
,
то существует и
то существует и
и обратно, если существует
,
то существует и
![]() Это и доказывает справедливость теоремы.
Это и доказывает справедливость теоремы.
Теорема
2.
Если ряд (1) сходится и его сумма равна
S,
то ряд
![]() ,
(2)
,
(2)
где с – число, также сходится и его сумма равна c.S.
Доказательство. Пусть Sn и sn – n-е частичные суммы соответственно рядов (1) и (2). Тогда
![]() .
.
Предел
sn
существует, так как
![]() =
=![]() =c.
=c.S,
что и требовалось доказать.
=c.
=c.S,
что и требовалось доказать.
Теорема 3. Если ряды
![]() и
и
![]() (3)
(3)
сходятся
и их суммы равны соответственно
![]() и S,
то ряды
и S,
то ряды
![]() (4)
(4)
и
(u1-v1)+
(u2-v2)+…+
(un-vn)+…![]() (5)
также
сходятся и их суммы равны соответственно
(5)
также
сходятся и их суммы равны соответственно
![]() +S
и
-S.
+S
и
-S.
Доказательство.
Докажем сходимость ряда (4). Обозначим
sn,
![]() и
Sn
– n-е
частичные суммы рядов (4), (1) и (2)
соответственно. Получим
и
Sn
– n-е
частичные суммы рядов (4), (1) и (2)
соответственно. Получим
sn=(u1+v1)+(u2+v2)+…+(un+vn)=(u1+u2+…+un)+(v1+v2+…+vn)= + Sn.
Переходя в этом равенстве к пределу при n®¥, получим
=![]() (
(![]() +
Sn)=
+
Sn=
+
Sn)=
+
Sn=![]() +
S.
+
S.
Таким образом, ряд (4) сходится и его сумма равна + S.
Аналогично доказывается, что ряд (5) сходится и его сумма равна -S. Сделайте это самостоятельно
2. Необходимый признак сходимости ряда
Теорема.
Если ряд сходится, то
un=0.
Доказательство.
Пусть ряд u1+u2+…+un…
сходится, то есть существует конечный
предел
![]() =S.
Тогда имеет место также равенство
=S.
Тогда имеет место также равенство
![]() =S,
так как при n
=S,
так как при n
![]() и
(n-1)
.
Вычитая
почленно из первого
равенства второе, получаем
и
(n-1)
.
Вычитая
почленно из первого
равенства второе, получаем
![]() -
=
-
=
![]() =
un=0,
что и требовалось доказать.
=
un=0,
что и требовалось доказать.
Следствие.
Если
![]() un≠0,
то ряд u1+u2+…+un…
расходится.
un≠0,
то ряд u1+u2+…+un…
расходится.
Пример.
Ряд
![]() расходится, так как
un=
расходится, так как
un=
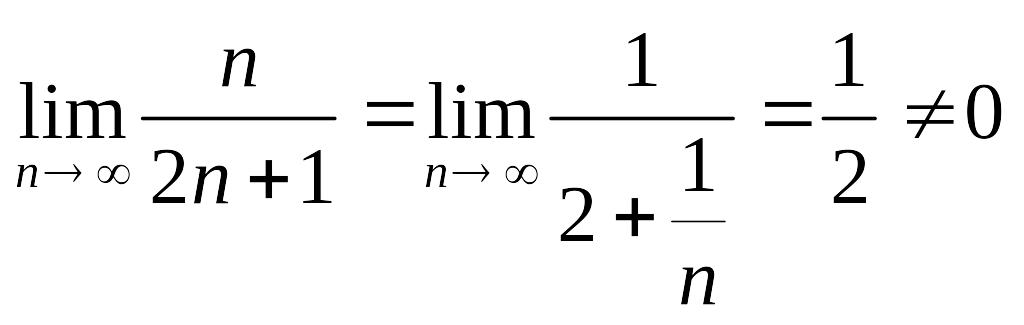 .
.
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что un=0 не следует, что ряд сходится.
Позже
докажем, что так называемый гармонический
ряд
![]() (6) расходится,
хотя
un=
(6) расходится,
хотя
un=
![]()
