
- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
5. Дифференциалы высших порядков
Дифференциалы
высших порядков.
Определение
1. Дифференциал
от первого дифференциала функции
называется вторым дифференциалом:
![]() Аналогично определяются дифференциалы
более старших порядков.
Аналогично определяются дифференциалы
более старших порядков.
Вычислим
второй дифференциал функции двух
переменных
![]() .
При этом будем считать, что дифференциалы
независимых переменных dx
и dy
– величины постоянные (т.е. не зависят
от т.(х,у)
и не меняются при вычислении каждого
последующего дифференциала).
.
При этом будем считать, что дифференциалы
независимых переменных dx
и dy
– величины постоянные (т.е. не зависят
от т.(х,у)
и не меняются при вычислении каждого
последующего дифференциала).
![]() .
.
Не
трудно видеть, что второй дифференциал
представляет собой квадратичную
форму
от переменных dx
и dy.
Матрица этой квадратичной формы есть
матрица Гессе, т.е. d2z
= (dx,dy)Г(dx,dy)T
(см. раздел «Линейная алгебра»,
квадратичные формы). Кроме того,
второй
дифференциал можно записать в символическом
виде:
![]()
Можно
показать, что в общем случае дифференциал
2 – го порядка функции u
= F(x)
равен
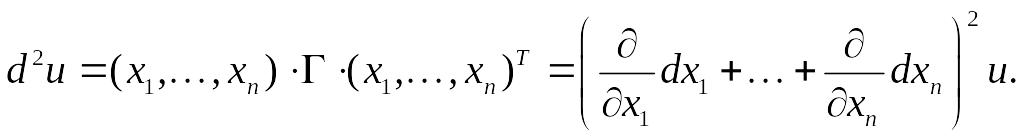
Дифференциал
m
– го порядка равен
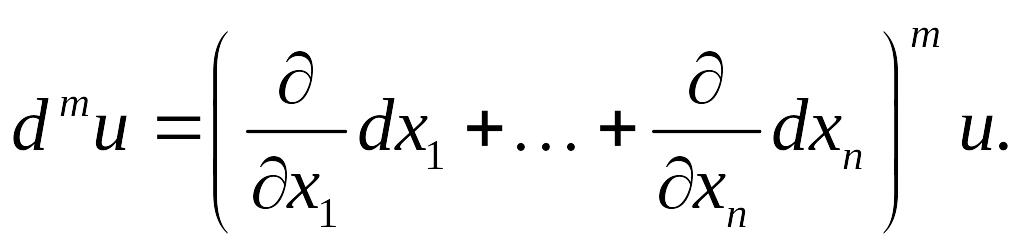
6. Дифференцирование сложных функций
Производная
сложной функции.
Рассматривается сложная функция
аргумента t
:
![]()
Теорема
1. Пусть
функции xţ
дифференцируемы в т.to
, а функция u
в соответствующей т. хо.
Тогда сложная функция u
= u(t1,…,tm)
дифференцируема в т.to
, а ее частные производные в этой точке
равны
![]()
{Доказательство
проведем для частного случая
![]() (Изменятся
только технические подробности) Пусть
(Изменятся
только технические подробности) Пусть
![]() приращение
t.
Функции х
и у
получат приращения
приращение
t.
Функции х
и у
получат приращения
![]() В свою очередь приращение u
равно:
В свою очередь приращение u
равно:
![]() Так
как o(Δt)
= o(Δσ)
, окончательно получаем:
Так
как o(Δt)
= o(Δσ)
, окончательно получаем:
![]() }
}
Инвариантность первого дифференциала.
х – независимая переменная:
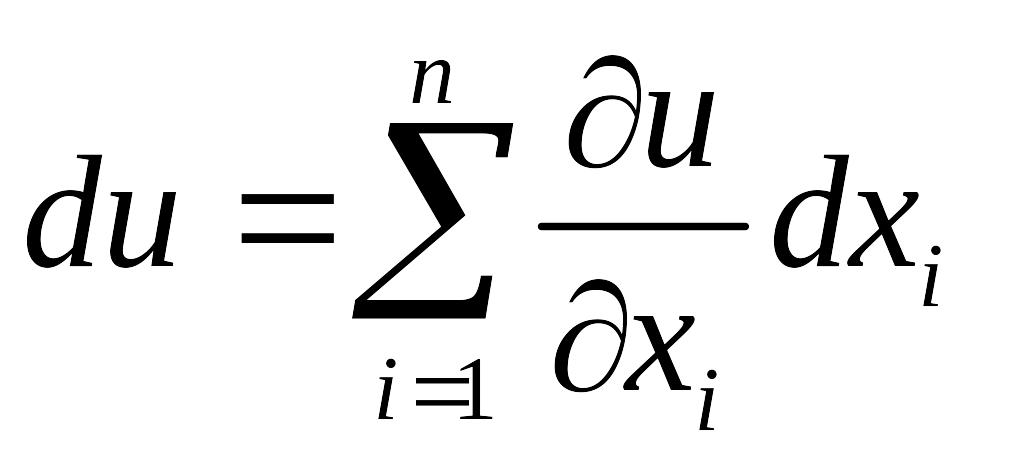 (§4).
(§4).хţ = φţ(t);
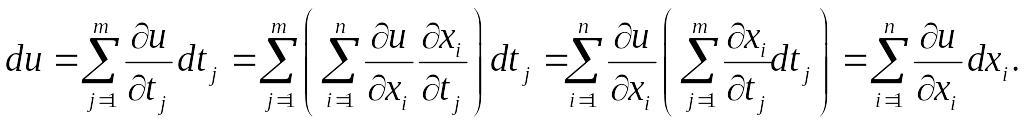
Таким образом, выражение для первого дифференциала не меняется, если переменная х является функцией другой переменной.
Замечание.
Дифференциалы 2 – го и более высоких
порядков, как и в случае одной переменной
не инвариантны, так как
![]() ,
если хţ
− функции (не линейные) новых переменных.
,
если хţ
− функции (не линейные) новых переменных.
7. Дифференцирование неявных функций
Неявные ФНП. Рассмотрим уравнение F(u, x1,…, xn) = 0. Будем считать, что по смыслу задачи u есть функция от переменных xţ : u = u(x1,…,xn). В этом случае говорят, что u задана неявно.
Примеры.
Теорема 1 (О существовании и дифференцируемости неявной функции). Пусть функция u задана уравнением F(u, x) = 0 и функция F(u, x) удовлетворяет следующим условиям:
F (u, x) дифференцируема в окрестности т. М0(u0, x0).
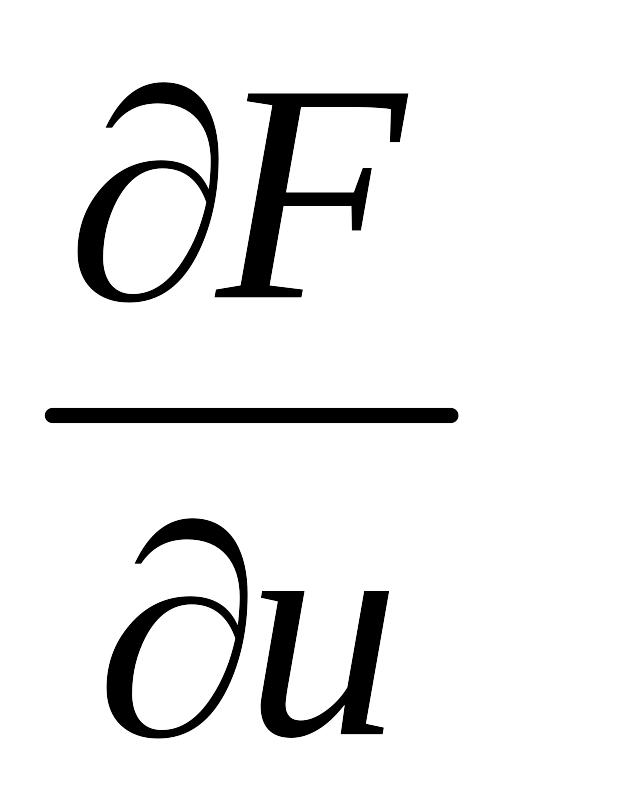 дифференцируема
в окрестности т. М0
.
дифференцируема
в окрестности т. М0
.F (u0, x0) = 0.
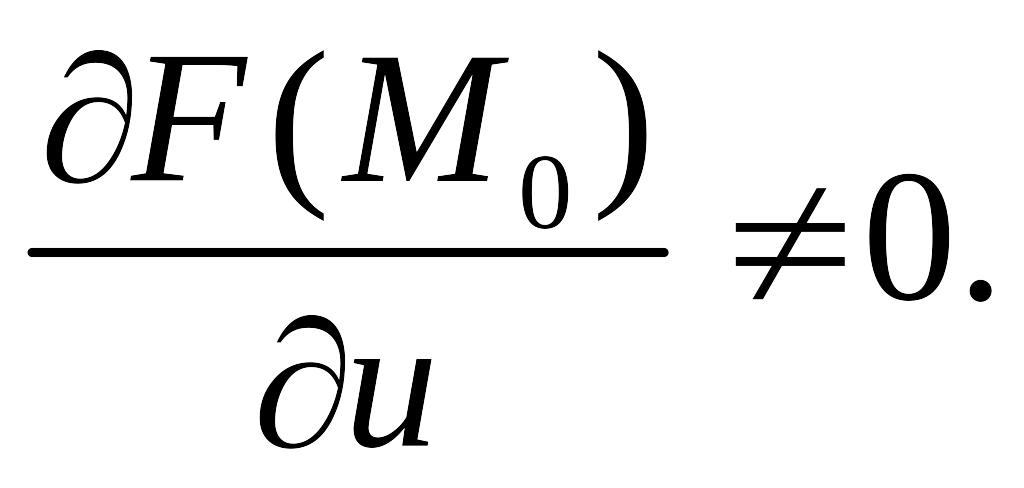
Тогда
для любого достаточно малого ε
> 0 найдется δ
> 0 , такое, что в
![]() определена
определена
единственная
дифференцируемая функция u
= f(x)
, удовлетворяющая условию
![]()
{без доказательства}
Для вычисления частных производных рассмотрим уравнение F(u, x, y) = 0. Пусть
u
=
u(x,
y)
– решение этого уравнения. Продифференцируем
тождество
![]()
по
х
:
![]() Отсюда получаем (для у
аналогично) :
Отсюда получаем (для у
аналогично) :
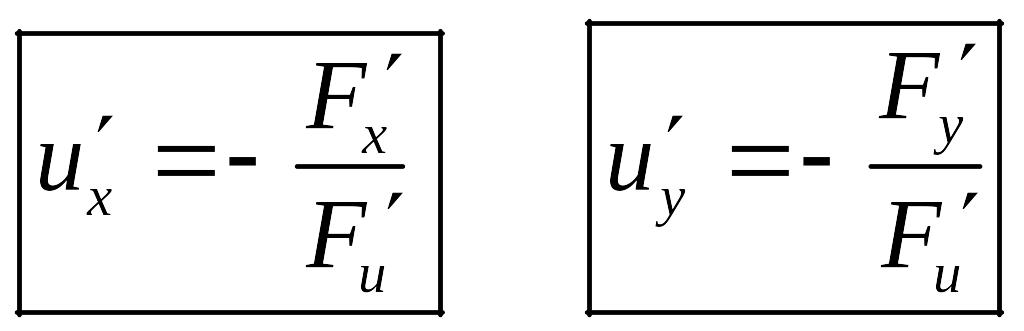
Пример.
Выведем уравнение касательной плоскости
к неявно заданной поверхности S:
F(x,
y,
z)
= 0 в т.
![]() .
Как известно, уравнение касательной
плоскости имеет вид :
.
Как известно, уравнение касательной
плоскости имеет вид :![]() .
Подставим в это уравнение значения
частных производных неявно заданной
функции. После простых преобразований
получим:
.
Подставим в это уравнение значения
частных производных неявно заданной
функции. После простых преобразований
получим:
![]()
Полная
производная.
Пусть
![]() функции
одной переменной. Тогда u
есть функция одной переменной t
и
функции
одной переменной. Тогда u
есть функция одной переменной t
и
![]() производная
по единственному аргументу, т.е. –
обычная
производная:
производная
по единственному аргументу, т.е. –
обычная
производная:
![]()
Рассмотрим
частный случай z
= f(x,
y),
y
= y(x).
Полная производная z
по х
равна:
![]()
Пример.
![]()
